R4内常平均曲率和常数量曲率超曲面

2023-11-23 理论教育版权反馈

【摘要】：本讲考虑4维欧氏空间R4内3维完备连通非零常平均曲率和非负常数量曲率超曲面．上一讲公式（1．6．61）以前的全部公式都可以在本讲应用．在本讲，H是非零常数．令利用上一讲上公式（1．6．2）及上式，有而且利用（1．7．1），有从下面开始，n＝3，C*＝0．即考虑R4内具有非零常平均曲率H和非负常数量曲率R的完备连通超曲面M．在M上的任一点P上，选择M的切向量e1，e2，e3，使得hij＝λiδij，

本讲考虑4维欧氏空间R4内3维完备连通非零常平均曲率和非负常数量曲率超曲面．上一讲公式（1．6．61）以前的全部公式都可以在本讲应用．

在本讲，H是非零常数．令

利用上一讲上公式（1．6．2）及上式，有

而且

利用（1．7．1），有

从下面开始，n＝3，C*＝0．即考虑R4内具有非零常平均曲率H和非负常数量曲率R的完备连通超曲面M．在M上的任一点P上，选择M的切向量e1，e2，e3，使得hij＝λiδij，由公式（1．7．1），在这点P上

这里选择e4，使得非零常平均曲率H＞0．

利用上一讲公式（1．6．2）的第一式及本讲公式（1．7．7），在这点上，有

倒写上式，再利用（1．7．8）和（1．7．9），可以得到

由（1．7．2）的第二式，（1．7．6），（1．7．7）和（1．7．11），可以知道在M的每一点上，trace B4等于（1．7．11）右端的常数．

由公式（1．7．5）及上面的叙述，有

利用上一讲公式（1．6．61）以及上式，注意到C*＝0，n＝3，有

Codazzi方程组，可以得到第二个等式）

由上式，利用因式公解，立即有

因而引理1的结论成立．

利用第1讲公式（1．1．19），并注意到欧氏空间的曲率为零，有M的Ricci曲率

在本讲，n＝3，在M的任意一点P，有

即M的Ricci曲率有下界，可以利用完备连通Riemann流形的广义最大值原理（见第5讲）．

下面要证明一个定理．

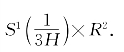
定理6　在R4内，设M是完备连通（等距浸入）超曲面，具有正常平均曲率H和非负常数量曲率R，那么，只有三种情况：R＝6H2，M＝；R＝，M＝×R；R＝0，有例M＝ pagenumber_ebook=118,pagenumber_book=110

注：M是非零常平均曲率H时，可选择M的单位法向量，使得H是一个正常数．

证明　由于这时M的第二基本形式长度平方S也是常数，又由于R≥0，利用上一讲公式（1．6．4）及C*＝0，n＝3，有

由Cauchy不等式，有

当常数S＝时，本讲引理1推导过程中一切不等式都取等号，再由上一讲引理1知道，在M的每点上，μ1，μ2，μ3只有两个不同的值，注意到上一讲引理1取最大值的条件（由于公式（1．7．38）取等号），不妨设在M的某点P处，

利用公式（1．7．9）以及上式，在点P，有

由上式和公式（1．7．7），在点P，有

于是，λ1λ2，λ1λ3，λ2λ3都是非负常数．由第1讲内公式（1．1．19）（Gauss方程组）可以知道，M的截面曲率处处是非负常数．类似第3讲中的证明，利用Frobenius定理，M的每个局部都是×R，这里R是一条欧氏直线．由于M是完备连通的，则M就是×R．

下面考虑正常数S＞的情况．利用公式（1．7．30）的f的定义可以知道，f是M上有上界的光滑函数．利用第5讲完备连通Riemann流形的广义最大值原理，在M上有一个点列｛Pv|v∈N｝，这里N是全体正整数组成的集合，满足

由公式（1．7．3），（1．7．6）和（1．7．7）可以知道

又利用公式（1．7．31）和（1．7．50），以及H＞0，可以知道

再利用公式（1．7．4），（1．7．6）和（1．7．7），有

这里兼顾上一讲引理1，以及本讲公式（1．7．2）和（1．7．3），可知上式后一个不等式成立．

先证明（1），用反证法，如果（1）不成立，利用（1．7．53），有

明显地，

这里利用了（Pv）（j＝1，2，3）两两不相等．(www.chuimin.cn)

由于H，S都是正常数，公式（1．7．31）两端微分，有

利用公式（1．7．50）的第二式及上式，有

利用正常数H，S的定义，求导后，在M的任意一点P处，有

这里利用了在点P，hij＝λiδij．下标l∈｛1，2，3｝．

利用上一讲公式（1．6．49）的推导过程中相同的理由，在点P，有

这里l∈｛1，2，3｝．记

利用公式（1．7．59），（1．7．61）和（1．7．62），有

对固定下标l，公式（1．7．60）及（1．7．62）组成了一个关于h11l，h22l，h33l的线性方程组，再利用公式（1．7．56），有

由公式（1．7．57），（1．7．63）和（1．7．64），有

明显地，有

这里利用了Codazzi方程组．当下标i，j，k两两不相等时，有μi＋μj＋μk＝μ1＋μ2＋μ3＝0（利用公式（1．7．8）），再利用Codazzi方程组，简化上式，有

利用公式（1．7．65）和（1．7．67），有

类似公式（1．7．66）和（1．7．67），可以看到

利用公式（1．7．65）和（1．7．69），有

公式（1．7．34）两端在Pv取值，并且令v→∞，利用公式（1．7．50）的第一式、第三式，以及（1．7．68），有

类似上一讲公式（1．6．105），可以看到

利用公式（1．7．30），有f≤0．上式两端在点Pv处取值，再令v→∞，利用结论（1），有

下面考虑f是常数的情况．利用公式（1．7．31），可以看到这时M上任意一点处，都是常数．由于H，S都是正常数，则λ1，λ2，λ3也都是常数，M是R4内等参超曲面（可参考上一讲结束部分）．

现在考虑非负常曲率C*空间内n维等参超曲面M，在第3讲内已经提及它，这时，存在M的局部分正交标架场e1，e2，…，en，使得矩阵（hij）是常数对角矩阵．利用第3讲内公式（1．3．66）于超曲面情况，有

由于S，hij都是常数，上式左端及右端第一大项都是零．于是，在M上，处处有

利用第3讲内公式（1．3．89）—（1．3．93），可以看到：当hii≠hjj时，ωji＝0；当ωji≠0时，必有hii＝hjj．利用第3讲内公式（1．3．94）的第一式，当hii≠hjj时，有

这里

完全类似第3讲内公式（1．3．96）的证明，可以知道，（1．7．84）的右端的第一大项等于零．于是，利用（1．7．84）和（1．7．85），有

于是，当hii≠hjj时，必有

特别地，当C*＝0时，表明不相等的两常数hii，hjj中必有一个是零．因此，对于Rn＋1内等参超曲面M，如果不是全脐点超曲面，全部n个常数hjj（1≤j≤n）只有两个值：一个是零，一个是非零．不妨设

顺便提一下，上一讲最后提及的Sn＋1（1）内极小超曲面是等参超曲面时，当M是全脐点时，M必是超球面Sn（1）片；当M不是全脐点时，利用公式（1．7．87）可知，全部h11，h22，…，hnn也只有两个值，互为负倒数．有兴趣的读者可自己去确定Sn＋1（1）内极小等参超曲面．

编者的话

本讲是根据作者在《数学年刊》1985年发表的一篇文章写成的（［2］）．

关于欧氏空间内常平均曲率和常数量曲率超曲面，有一些后续工作．例如在1987年，孙自琪证明了：设M是R4内具有非零常平均曲率H和常数量曲率R的完备连通超曲面，如果M不是等参超曲面，则必有R＜0．

参考文献

［1］Okumura，M．．Hypersurfaces and a pinching problem on the second fundamental tensor．Amer．Jour．of Math．，Vol．96（1974）：207-213．

［2］黄宣国．Complete hypersurfaces with constant scalar curvature and constant mean curvature in R4．数学年刊（B辑），第6卷第2期（1985）：177—184．

R4内常平均曲率和常数量曲率超曲面

相关推荐