线性空间同构证明及相关性质

2023-11-22 理论教育版权反馈

【摘要】：，σ（αn）是线性无关的.因此，n≤m.综合上面的结论可以得到n=m，即V1，V2有相同的维数.充分性.设V1，V2都是n维线性空间，下面我们来建立一个从V1到V2的同构映射，从而证明V1V2.分别取V1的一组基α1，α2，…，αn之下的坐标是唯一确定的，而向量组β1，β2，…

本节研究线性空间的同构问题，即本质上相同的线性空间应该如何刻画.最终我们得到的结论是维数相同的线性空间一定是相互同构的，因此维数是线性空间的本质特征.

定义4.10 设V₁和V₂是数域F上的线性空间，σ是从V₁到V₂的一个双射，且满足条件：

（1）σ（α+β）=σ（α）+σ（β），对任意的α，β∈V₁；

（2）σ（kα）=kσ（α），对任意的α∈V₁，k∈F，

这时称V₁和V₂是同构的，记作V₁≅V₂，σ称为从V₁到V₂的同构映射.

同构的线性空间不仅元素之间有一一对应关系，而且还保持元素之间的线性运算关系.因此，同构的线性空间可以认为是一样的.

命题4.10 线性空间的同构是等价关系，即

（1）反身性 V₁≅V₁；

（2）对称性若V₁≅V₂，则V₂≅V₁；

（3）传递性若V₁≅V₂且V₂≅V₃，则V₁≅V_3.

证明留作习题.

命题4.11 设σ是从V₁到V₂的同构映射，则σ（0）=0.

证明：由于

σ（0）=σ（0+0）=σ（0）+σ（0），

得σ（0）=0.证毕.

定理4.12 两个线性空间同构的充分必要条件是它们的维数相等.

证明：必要性.设线性空间V₁≅V₂，且V₁，V₂的维数分别是n，m，σ是从V₁到V₂的同构映射.

首先，取V₂的一组基

β₁，β₂，…，β_m，

因为σ是同构映射，所以，σ是满射.这样，存在V₁中的向量

α₁，α₂，…，α_m，

使得

σ（α_i）=β_i，1≤i≤m.

下面证明向量组α₁，α₂，…，α_m是线性无关的.设

则

于是，可以得到k_i=0，1≤i≤m，即得α₁，α₂，…，α_m线性无关，因此，m≤n.

另一方面，取V₁的一组基

α₁，α₂，…，α_n，(www.chuimin.cn)

下面来证明向量组

σ（α₁），σ（α₂），…，σ（α_n）

也是线性无关的.设

则有

由于σ是同构映射，因此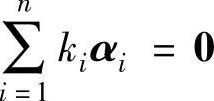.进而得到，k_i=0，1≤i≤n，即

σ（α₁），σ（α₂），…，σ（α_n）

是线性无关的.因此，n≤m.

综合上面的结论可以得到n=m，即V₁，V₂有相同的维数.

充分性.设V₁，V₂都是n维线性空间，下面我们来建立一个从V₁到V₂的同构映射，从而证明V₁≅V_2.

分别取V₁的一组基α₁，α₂，…，α_n和V₂的一组基β₁，β₂，…，β_n，构造一个从V₁到V₂的映射σ，对V₁中任意的向量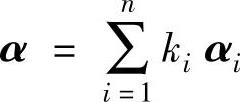，定义

由于V₁中每个向量在基α₁，α₂，…，α_n之下的坐标是唯一确定的，而向量组β₁，β₂，…，β_n是V₂的一组基，因此这个映射的定义是合理的.

对于V₂中任意向量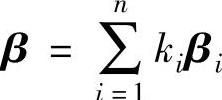，取，则有σ（α）=β，即映射σ是满射.

任取V₁中的两个向量

若σ（α）=σ（α′），即

则k_i=l_i，1≤i≤n，因此α=α′，所以映射σ是单射.

综合上面结论，映射σ是双射.

容易验证，映射σ还满足条件：

σ（α₁+α₂）=σ（α₁）+σ（α₂）

及

σ（kα）=kσ（α），

对任意的α₁，α₂∈V₁，k∈F.因此映射σ是从V₁到V₂的同构映射，即V₁≅V₂.证毕.

推论4.6 数域F上的任一n维线性空间均同构于Fⁿ.

习题

4.8.1. 证明命题4.10.

4.8.2. （1）证明：复数域C作为实数域R上的线性空间是二维的，1和i是它的一组基；

（2）C⁰是习题4.1.2定义的线性空间.证明：C⁰≅C.

4.8.3. 证明线性空间R_n-1[x]同构于Rⁿ.

线性空间同构证明及相关性质

相关推荐