单项选择题74某设置有中央空调送风系统的建筑,其火灾自动报警系统中的点型火灾探测器至空调送风口和多孔送风顶棚孔口边缘的水平距离,分别不应小于( )m。按使用单位的改造要求,提出探测器设置和安装应该注意的问题。吸烟室不宜选用感烟探测器。......
2025-09-30
1.选择题.
(1)设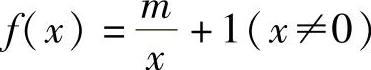 ,且f(1)=2,则f(2)=( ).
,且f(1)=2,则f(2)=( ).
(2)在区间0°≤α<360°中,与-330°的角终边相同的是( ).
A.150°B.210°C.30°D.330°
(3)若角α的终边上有一点P(3,-4),则下列等式中正确的是( ).
A.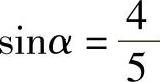
B.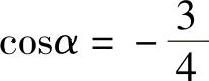
C.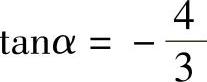
D.以上答案都不对
(4)使sinα·cosα<0成立的角α是( ).
A.第三、四象限角B.第一、三象限角C.第二、四象限角D.第一、四象限角
2.填空题.
(1)若f(x)=4-x,则f(-1)=.
(2)函数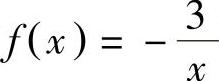 的图像关于对称.
的图像关于对称.
(3)若角α终边上一点的坐标是P(-1,2),则角α是第____象限角.
(4)与1991°终边相同的最小正角是____.
3.判断题.
(1)因为sin2α+cos2α=1,所以sin4α+cos4α=1; ( )
(2)sin4α-cos4α=sin2α-cos2α; ( )
(3)因为sin2α+cos2α=1,所以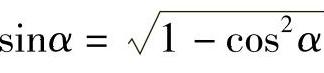 ;( )
;( )
(4)等式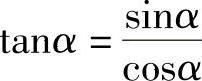 在任何条件下都成立.( )
在任何条件下都成立.( )
4.计算:(https://www.chuimin.cn)
(1)sin45°-cos60°+tan60°;
(2)cos230°+sin2302-tan45°;
(3)sin30°-tan30°+cos45°.
5.确定下列三角函数值的符号:
(1)cos250°; (2)sin(-45°); (3)tan(-672°); (4)tan660°.
6.已知角α的终边经过下列各点,试根据三角函数的定义,分别求出角α的三个三角函数值.
(1) ;
;
(2)P(1,-1).
7.画出下列函数在区间[0,2]上的简图:
(1)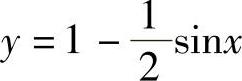 ;
;
(2)y=3cosx-1.
8.利用计算器求出下列三角函数值:
(1)sin368°34′;(2)cos(-167°);
(3)tan3.6;
(4)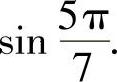
9.求出下列函数的最大值、最小值,并求出使函数取得最大值、最小值的x的集合:
10.弹簧挂着的小球作上下振动,它在ts时相对平衡位置(即静止时的位置)的高度为h(cm),由关系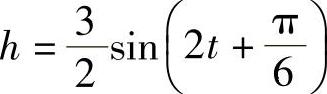 决定.试以t为横坐标,h为纵坐标,画出这个函数在长度为一个周期的闭区间上的图像,并回答以下问题:
决定.试以t为横坐标,h为纵坐标,画出这个函数在长度为一个周期的闭区间上的图像,并回答以下问题:
(1)小球在开始振动时(即t=0时)的位置在哪里?
(2)小球的最高点和最低点与平衡位置的距离分别是多少?
(3)经过多少时间小球往返振动一次?
(4)每秒钟小球能往返振动多少次?
相关文章

单项选择题74某设置有中央空调送风系统的建筑,其火灾自动报警系统中的点型火灾探测器至空调送风口和多孔送风顶棚孔口边缘的水平距离,分别不应小于( )m。按使用单位的改造要求,提出探测器设置和安装应该注意的问题。吸烟室不宜选用感烟探测器。......
2025-09-30

测量线段的长度显示方式有三种:长度、水平X、垂直Y。②继续单击线段,可显示每一段线的长度和累加线段的长度,如图3-51所示。测量一条线的水平夹角、垂直夹角:选中工具,鼠标在线上单击,再右键单击,弹出对话框,单击按钮即可。......
2025-09-29

在讨论单圆盘转子的振动中,是假定转子的质量集中在圆盘上,而略去了轴的质量。为了研究转子的横向弯曲振动,即图示在y方向的振动,取二集中质量在y方向的坐标为y1,y2,这两个坐标随时间变化的规律,就是整个转子在y方向的振动规律。由于转子作无阻尼的自由振动,因此振动中仍然是惯性与弹性力相平衡,设1和2两点的振动位移分别为y1、y2,则可列出振动微分方程组为式中,aij是影响系数。......
2025-09-30

电磁噪声与槽的配合、槽的斜度及电动机结构的刚度均有密切关系。(二)电梯振动与噪声引起电梯抖动、振动与噪声的主要原因如下。在降振、隔振中降低噪声。经过隔振处理后,振动级由原来的84dB可下降至75dB,机房室内噪声可由42dB下降到35dB。如果电梯有高频振动和共振现象,则要消除共振,才能消除噪声。......
2025-09-29

表4.4.3架空线路与邻近线路或设施的距离4.4.4配电线路,应遵守下列规定:1配电线路采用熔断器作短路保护时,熔体额定电流应不大于电缆或穿管绝缘导线允许载流量的2.5倍,或明敷绝缘导线允许载流量的1.5倍。......
2025-09-29

下面以一个简单的模型为例,来说明测量距离的方法以及相应的操作过程。Step1.打开文件D:\ug90\work\ch03.23\distance.prt。图3.23.1所示“测量距离”对话框的下拉列表中的部分选项说明如下:●:该选项用于测量点、线、面之间的任意距离。图3.23.1 “测量距离”对话框定义测量几何对象。操作方法参见Step3,先选取点1,后选取边线。图3.23.3 点到面的距离图3.23.4 点到线的距离Step6.测量线到线的距离。选取图3.23.7a中的模型表面1。......
2025-09-30

续表考点:圆的方程(2016卷II,4)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=().A.-B.-C.D.21.已知圆C:(x-1)2+(y-2)2=2与y轴在第二象限所围区域的面积为S,直线y=2x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=().A.-B.±C.-D.±2.(2016河南洛阳四模)距某码头400km......
2025-09-30

前面阐述了认知目标和试题之间准确对应的重要意义,但这种对应应当是“有弹性的对应”,如表5-2所示,一个认知目标可能涵盖多种任务途径。然而正如本节开头所指出的,目前我国大规模测试中,能力目标与试题之间的对应存在过于简单化,甚至有些僵化的现象。试题题干的表达与认知目标的表述保持适度距离,会是怎样的效果?我们看到的是一系列指向文本本身的具体问题,认知目标隐藏于问题引发的阅读过程和行为中。......
2025-09-29
相关推荐