保险正是针对危险而建立的一种经济制度。然而,保险也不可能对一切危险都予以承保。因此,将来确定发生的危险、已经发生的危险事故、投机性危险等均不被列入保险的适用范围。一旦发生被保险标的损失,由保险基金加以赔偿。人身保险是指以人的生命、身体或健康为保险标的的一种保险,如人寿保险、健康保险、意外伤害保险。原保险又称“第一次保险”“基础保险”,是指保险人对被保险人因保险事故所致损害承担......
2023-07-27
一、区间与邻域
1.区间
定义1.1 满足不等式a<x<b(a<b)的所有实数x的集合,称为以a、b为端点的开区间,记作(a,b).
类似地,有闭区间[a,b]={x|a≤x≤b},半开区间(a,b]={x|a<x≤b}和[a,b)={x|a≤x<b},它们称为有限区间.而区间(a,+∞)、[a,+∞)、(-∞,a)、(-∞,a]称为无限区间.
2.邻域
定义1.2 设a∈R,δ>0,数集{x|x-a<δ}称为a的δ邻域,记为
U(a,δ)={x||x-a<δ}=(a-δ,a+δ).
a称为邻域的中心;δ称为邻域的半径.常又表示为U(a),简称为a的邻域.
去掉中心a的数集{x|0<x-a<δ}称为a的去心δ邻域,记为
U°(a,δ)={x|0<x-a<δ}=(a-δ,a+δ)-{a}.
常又表示为U°(a),简称为a的去心δ邻域.
类似地,数集{x|0<x-a<δ}称为a的右邻域,数集{x|-δ<x-a<0}称为a的左邻域.
二、函数概念
1.变量
在研究数学的过程中常常涉及到各种各样的量,其中,变化的量称为变量,不变化的量称为常量或常数.函数是考察变量之间关系的重要概念.
例如,球的半径r与该球的体积V的关系为
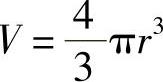
式中,π是圆周率,它是常量.
对于任意r∈[0,+∞),都对应一个球的体积V.r和V都是变量,它们之间的关系可以用函数来表达.
2.函数定义
定义1.3 设D是非空数集,若对D中任意数x(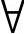 x∈D),按照某一确定的对应法则f,总有唯一确定的数y∈R与之对应,则称f是定义在D上的函数,记为
x∈D),按照某一确定的对应法则f,总有唯一确定的数y∈R与之对应,则称f是定义在D上的函数,记为
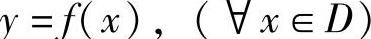
简写为“y=f(x)”,或称“f(x)是x的函数(值)”.其中,数x称为自变量,数y称为因变量.
数集D称为函数f的定义域,函数值的集合f(D)={f(x)|x∈D}称为函数f的值域.函数的两要素为定义域和对应法则,与变量用何符号表示没有关系.
3.单值函数与多值函数
在函数y=f(x)的定义中,要求对应于x值的y值是唯一确定的,这种函数也称为单值函数.如果取消唯一这个要求,即对应于x值,可以有两个以上确定的y值与之对应,那么函数y=f(x)称为多值函数.例如,函数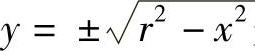 是多(双)值函数.
是多(双)值函数.
以后若不特别声明,只讨论单值函数.
4.函数举例
例1 取整函数y=[x],表示对于任意x∈R,对应的y是不超过x的最大整数.
如[2.5]=2,[3]=3,[0]=0,[-π]=-4,图形(见图1-1).
例2 符号函数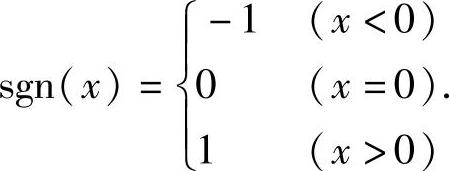
例3 绝对值函数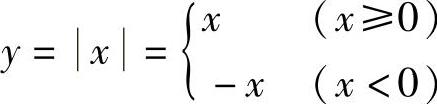 ,图形(见图1-2).
,图形(见图1-2).

图1-1
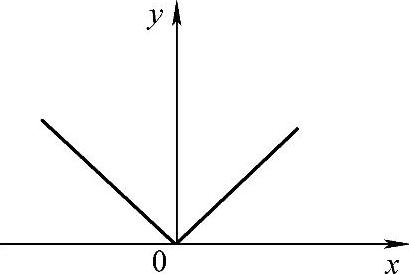
图1-2
上述几个函数的定义域被分成了若干部分,而在不同部分上,函数值用不同的表达式表示,这样的函数称为分段函数.
三、函数性质
1.有界性
定义1.4 设函数f(x)在数集A上有定义,若存在M>0,使得任意x∈A,有f(x)≤M,则称函数f(x)在A上有界,否则称f(x)在A上无界.
例如,函数y=sinx在(-∞,+∞)内是有界的,因为对于任意x∈R,都有|sinx≤1.函数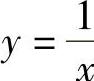 在(0,1)内是无界的,在[2,+∞)上是有界的.
在(0,1)内是无界的,在[2,+∞)上是有界的.
2.单调性
定义1.5 设函数f(x)在数集A上有定义,若对任意x1,x2∈A,当x1<x2时,有f(x1)<f(x2)(或f(x1)>f(x2)),则称函数f(x)在A上是严格单调增加(或严格单调减少)的;若将上述不等式改为f(x1)≤f(x2)(或f(x1)≥f(x2)),则称函数f(x)在A上是单调增加(或单调减少)的.
例如,函数y=x3在(-∞,+∞)内是严格单调增加的.函数y=2x2+1在(-∞,0)内是严格单调减少的,在[0,+∞)内是严格单调增加的.因此,y=2x2+1在(-∞,+∞)内不是单调函数.
3.奇偶性
定义1.6 设函数f(x)定义在数集A上,若对于任意x∈A,有-x∈A,且
f(-x)=-f(x)(或f(-x)=f(x))
则称函数f(x)是奇函数(或偶函数).奇函数的图像关于原点对称,偶函数的图像关于y轴对称.(www.chuimin.cn)
例如,函数y=x4+3x2,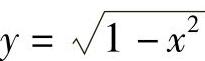 ,
, 都是偶函数.函数y=
都是偶函数.函数y= ,y=x3,y=xcosx都是奇函数.
,y=x3,y=xcosx都是奇函数.
4.周期性
定义1.7 设函数f(x)定义在数集A上,若存在l>0,对于任意x∈A,有x±l∈A,且f(x±l)=f(x),则称函数f(x)是周期函数,l称为函数f(x)的周期.
由定义可知,周期不唯一.若l是函数f(x)的周期,则2l也是它的周期,nl(n∈N)也是它的周期.若函数f(x)有最小的正周期,通常称之为函数f(x)的基本周期,简称为周期.
例如,正弦函数y=sinx就是周期函数,周期为2π.再如,常数函数y=1也是周期函数,任意正实数都是它的周期,它没有基本周期.
四、复合函数与反函数
1.复合函数
定义1.8 设函数z=f(y)定义在数集B上,函数y=φ(x)定义在数集A上,且φ(A)⊂B(φ(A)是B的一个非空子集).对于任意x∈A,按照对应关系φ,对应唯一一个y∈B,若再按照对应关系f,对应唯一一个z,即对于任意x∈A,对应唯一一个z.于是可以在A上定义一个函数,表示为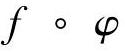 ,称为函数y=φ(x)与z=f(y)的复合函数,即
,称为函数y=φ(x)与z=f(y)的复合函数,即
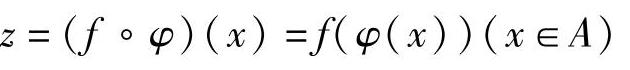
其中,y称为中间变量.
例如,函数 的定义域是区间[0,+∞),函数y=1-x2的定义域是R.为使其生成复合函数,必须要求
的定义域是区间[0,+∞),函数y=1-x2的定义域是R.为使其生成复合函数,必须要求
y=1-x2≥0,即-1≤x≤1于是,对于任意x∈[-1,1],函数y=1-x2与 生成了复合函数
生成了复合函数
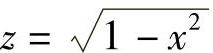
又如,3个函数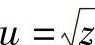 ,z=lny,y=2x+3,生成的复合函数是
,z=lny,y=2x+3,生成的复合函数是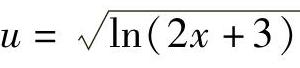 ,x∈[-1,+∞).
,x∈[-1,+∞).
2.反函数
定义1.9 设函数y=f(x),x∈I.若对任意y∈f(I),有唯一确定的x∈I与之对应,使f(x)=y,则在f(I)上定义了一个函数,记为
x=f-1(y),y∈f(I)
称为函数y=f(x)的反函数.原来的函数y=f(x)称为直接函数.
按照书写习惯,将自变量写成x,因变量写成y,所以反函数x=f-1(y)常常被写作y=f-1(x).
反函数y=f-1(x)的图像与直接函数y=f(x)的图像关于直线y=x对称(见图1-3).

图1-3
定理1.1 若函数y=f(x)在某区间I上严格单调增加(或严格单调减少),则函数y=f(x)存在反函数,且反函数x=f-1(y)在f(I)上也严格单调增加(或严格单调减少).
定理1.1中“严格”两字不可忽略.如单调函数y=[x](取整函数)非严格单调,不存在反函数.
函数是严格单调的仅是存在反函数的充分条件,如函数
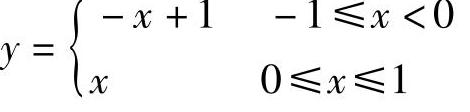
在区间[-1,1]上不是单调函数,但它存在反函数
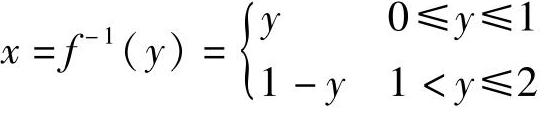
五、初等函数
1.基本初等函数
(1)常数函数
y=C;
(2)幂函数
y=xα;
(3)指数函数
y=ax,(a>0,a≠1).特例y=ex;
(4)对数函数
y=logax,(a>0,a≠1).特例y=lnx;
(5)三角函数
y=sinx,y=cosx,y=tanx,y=cotx,y=secx,y=cscx;
(6)反三角函数
y=arcsinx,y=arccosx,y=arctanx,y=arccotx.
2.初等函数的定义
定义1.10 由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所生成的并可用一个式子表达的函数称为初等函数.
例如,函数 是一个初等函数,它是由y=sinu,u=lnv,
是一个初等函数,它是由y=sinu,u=lnv,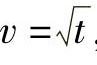 ,t=x2-1经过四则运算及复合而得.
,t=x2-1经过四则运算及复合而得.
由定义可知,那些不能用一个式子表达的分段函数,都不是初等函数.
有关高等数学(上、下册)的文章

保险正是针对危险而建立的一种经济制度。然而,保险也不可能对一切危险都予以承保。因此,将来确定发生的危险、已经发生的危险事故、投机性危险等均不被列入保险的适用范围。一旦发生被保险标的损失,由保险基金加以赔偿。人身保险是指以人的生命、身体或健康为保险标的的一种保险,如人寿保险、健康保险、意外伤害保险。原保险又称“第一次保险”“基础保险”,是指保险人对被保险人因保险事故所致损害承担......
2023-07-27

金属在大气条件下发生腐蚀的现象,是最普遍的一种环境腐蚀形式。根据大气腐蚀的发生情况,我国大致可分为5种区域类型。多数情况下,大气腐蚀是由于潮湿的气体在物体表面形成一薄层液膜而引起的。金属材料在不直接被雨淋时发生的腐蚀破坏就是潮大气腐蚀的例子。......
2023-06-22

常指一个装备、工作机器等,其作用是完成特定的技术要求。又称调节器、控制装置,由控制元部件组成,它接受指令信号,输出控制作用信号于受控对象。如果干扰产生在系统内部,称为内扰;产生在系统外部,称为外扰。是指被控量经测量元件检测后回馈送到系统输入端的信号。是指给定值与被控量的差值,或指令信号与反馈信号的差值。又称为控制量,是指作用于被控对象的信号。......
2023-06-28

(一)定义混凝土是以胶凝材料、粗集料、细集料和水,必要时掺入化学外加剂和矿物质混合材料,按适当比例配合,经过均匀拌制、密实成型及养护硬化后得到的人工石材。以水泥为胶凝材料、砂石为集料的混凝土称为水泥混凝土,在建筑工程中最为常用。(二)分类根据不同的分类标准,混凝土可分为以下种类。钢筋混凝土强度高,耐久性好。......
2023-11-07

根据现场的完整真实程度现场分为:1.原始现场原始现场是指事故发生以后,在现场的车辆和遗留下来的一切物体、痕迹仍保持着事故发生的原始状况没有变动和破坏的现场,常被称为第一现场。......
2023-08-10

长期发音功能亢进之后,发音功能低下的患者因声带肌群收缩无力,声门闭合欠佳,且声带张力低下,导致音调下降。职业性用嗓人群或者儿童由于嗓音的滥用和误用,使声带长期处于超负荷运动中,造成声带的损伤,声带振动规律性及声门闭合程度下降,也容易导致音质异常。......
2023-07-02

(一)口吃的定义近十年来,不同的学者对口吃的定义不同。(二)口吃的发生率口吃的发病率因年龄、语言以及地域而不同。在言语治疗欠发达、欠普及的地区,口吃发病率比较高。口吃开始的年龄平均为3岁,少数发病于6岁后。参考杨淑兰口吃发生原因的理论、发病原因和机制可归纳为以下几类。......
2023-07-02

又如,有的汽车损失保险条款规定汽车发生保险事故以修为主,而有的汽车损失保险条款规定汽车发生保险事故以换为主,非保险公估人是不论保险合同是如何约定的,均按本行业规定评估与鉴定。一旦发生保险事故,被保险人就立即通知保险公估人进行查勘与定损。......
2023-08-10
相关推荐