证明AB行向量γi的关键依据

2025-09-30 理论教育版权反馈

【摘要】：，αs）.这是证明的关键依据.将B，AB 按行分块为，于是所以AB 的行向量γi（i＝1，2，…，αs＋βs］.因αi＋βi（i＝1，2，…，s）均可由向量组α1，α2，…，αp 扩充成［A，B］的极大线性无关组，设为α1，α2，…

（1）设A是m×n矩阵，则0≤r（A）≤min｛m，n｝（由定义）.

（2）设A是m×n矩阵，则r（kA）＝r（A）（k≠0）（由定义）.

（3）设A是m×n矩阵，P，Q分别是m 阶、n阶可逆矩阵，则

r（Α）＝r（PA）＝r（AQ）＝r（PAQ）.

【注】若r（AB）＜r（A），B为n 阶矩阵，则r（B）＜n.

（4）设A是m×n矩阵，B是n×s矩阵，则r（AB）≤min｛r（A），r（B）｝.

【注】证对于向量组α1，α2，…，αs及β1，β2，…，βt，若任一βi（i＝1，2，…，t）均可由α1，α2，…，αs线性表出，则r（β1，β2，…，βt）≤r（α1，α2，…，αs）.这是证明的关键依据.

将B，AB 按行分块为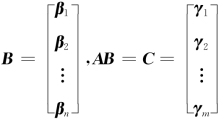 pagenumber_ebook=68,pagenumber_book=60 ，于是

所以AB 的行向量γi（i＝1，2，…，m）均可由B的行向量线性表出，故

r（AB）≤r（B）.

同理可证r（AB）≤r（A），故有r（AB）≤min｛r（A），r（B）｝.

（5）设A，B为同型矩阵，则r（A＋B）≤r（［A，B］）≤r（A）＋r（B）.

【注】证设r（A）＝p，r（B）＝q，将A，B按列分块为

A＝［α1，α2，…，αs］，B＝［β1，β2，…，βs］，

于是［A，B］＝［α1，α2，…，αs，β1，β2，…，βs］，

A＋B＝［α1＋β1，α2＋β2，…，αs＋βs］.

因αi＋βi（i＝1，2，…，s）均可由向量组α1，α2，…，αs，β1，β2，…，βs 线性表出，故

r（A＋B）≤r（［A，B］）.

又设A，B的列向量组的极大线性无关组分别为α1，α2，…，αp 和β1，β2，…，βq，将A的极大线性无关组α1，α2，…，αp 扩充成［A，B］的极大线性无关组，设为α1，α2，…，αp，β1，β2，…，βw，显然w≤q，故有

r（［A，B］）＝p＋w≤p＋q＝r（A）＋r（B），

故r（A＋B）≤r（［A，B］）≤r（A）＋r（B）.

（6）设A是m×n矩阵，B是s×t矩阵，则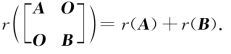 pagenumber_ebook=69,pagenumber_book=61

（7）设A，B，C均是n 阶方阵， pagenumber_ebook=69,pagenumber_book=61

【注】证 r（A）＋r（B）＝r（［A，O］）＋r（［O，B］）

（8）设A是m×n矩阵，B是n×s矩阵，则r（AB）≥r（A）＋r（B）－n.

【注】证对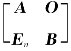 pagenumber_ebook=69,pagenumber_book=61 作初等变换，

又显然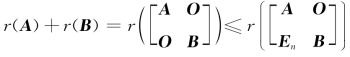 pagenumber_ebook=69,pagenumber_book=61 （局部≤整体），则

所以r（AB）≥r（A）＋r（B）－n.

这证明涉及分块矩阵的初等变换，可不作要求.

特别地，当AB＝O时，r（A）＋r（B）≤n，其中n是A 的列数（或B的行数）.

（9）设A是m×n实矩阵，则r（A）＝r（AT）＝r（AAT）＝r（ATA）.

【注】（1）设A是m×n实矩阵，AT是A的转置矩阵.证明：方程组（Ⅰ）Ax＝0和（Ⅱ）ATAx＝0是同解方程组.

证 ①若存在x，使Ax＝0，则两端左乘AT，得ATAx＝0，故方程组（Ⅰ）的解必是方程组

（Ⅱ）的解.

②若存在x，使ATAx＝0，则两端左乘xT，得xTATAx＝（Ax）TAx＝0.

因A 是实矩阵，故Ax是实向量.设Ax＝［a1，a2，…，am］T，则，得ai＝0（i＝1，2，…，m），故Ax＝0，从而知方程组（Ⅱ）的解必是方程组（Ⅰ）的解.

由①，②知，方程组（Ⅰ），（Ⅱ）是同解方程组.

（2）方程组Ax＝0和ATAx＝0是同解方程组，从而有r（A）＝r（ATA）.

（3）因r（A）＝r（AT），故r（A）＝r（AT）＝r（ATA）＝r（AAT）.

（10）设A是n 阶方阵，A是A的伴随矩阵.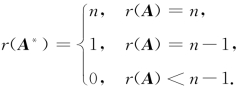 pagenumber_ebook=70,pagenumber_book=62

【注】分析证明前，①应先研究已知条件及其等价条件是什么.例如，已知r（A）＝n（应联想到）⇔≠0⇔A可逆⇔A的列向量组、行向量组线性无关⇔Ax＝0只有零解等.

r（A）＝n－1，应想到，但存在n－1阶子式不为零，故至少有一个中元素的余子式或代数余子式不为零.(https://www.chuimin.cn)

r（A）＜n－1，则中全部元素的代数余子式都为零.

②再研究要证什么.要证r（A）＝n，可证|A|≠0，证A可逆，证Ax＝0只有零解，且应想到A是什么样的矩阵.

③已知条件和要证结论之间有何种联系：

证当r（A）＝n时，A可逆，，由知，A和A均是可逆矩阵，故r（A）＝n.（或两边取行列式，得

当r（A）＝n－1时，由矩阵的秩的定义知，|A|中存在n－1阶子式不等于零，而A由|A|的元素aij 的代数余子式Aij 组成，故r（A）≥1.又r（A）＝n－1，，得r（A）＋r（A）≤n，而r（A）＝n－1，故r（A）≤1（或A的每一列均是Ax＝0的解向量，因r（A）＝n－1，故r（A）≤1），所以r（A）＝1.

当r（A）＜n－1时，由A 的秩的定义知，|A|的代数余子式全部为零，即A的全部元素为零，A＝O，故r（A）＝0.

对于以上证明有以下三点需考生注意.

①上述过程是可逆的，即

r（A）＝n⇔r（A）＝n，r（A）＝n－1⇔r（A）＝1，r（A）＜n－1⇔r（A）＝0.

考题也考过这些.

②A的秩只有三种情况：n，1，0.对行（列）向量组而言，A只有三种情况：n行（列）线性无关；n行（列）两两成比例；行（列）向量全部是零向量.

③进一步地，关于（A）的结论，见下例.

设A为n（n＞1）阶方阵，证明：

（1）n＝2时，（A）＝A；

（2）n＞2时，若A是可逆矩阵，则（A）＝|A|n－2A；

（3）n＞2时，若A是不可逆矩阵，则（A）＝O.

证（1）设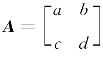 pagenumber_ebook=70,pagenumber_book=62 ，则

（2）由A＝|A|A－1，得（A）＝|A|（A）－1，又|A|＝|A|n－1，故

（3）此时r（A）＜n.

①若r（A）＜n－1，则由上述证明知，此时A＝O，故（A）＝O；

②若r（A）＝n－1，则由上述证明知，此时r（A）＝1＜n－1，于是（A）＝O.

综上所述，此时（A）＝O.

（11）设A是n 阶方阵，A2＝A，则r（A）＋r（A－E）＝n.

【注】证由A2＝A，得A（A－E）＝O，故r（A）＋r（A－E）≤n.

又r（A）＋r（A－E）＝r（A）＋r（E－A）≥r（A＋E－A）＝r（E）＝n，得证r（A）＋r（A－E）＝n.

（12）设A是n 阶方阵，A2＝E，则r（A＋E）＋r（A－E）＝n.

【注】证由A2＝E 得

（A＋E）（A－E）＝A2－E＝O，

于是有

r（A＋E）＋r（A－E）≤n.

注意到r（A－E）＝r（－A＋E），则

r（A＋E）＋r（A－E）＝r（A＋E）＋r（－A＋E）

≥r（A＋E－A＋E）

＝r（2E）＝n.

综上所述，r（A＋E）＋r（A－E）＝n得证.

（13）设A是m×n矩阵，则Ax＝0的基础解系所含向量的个数s＝n－r（A）.

（与第5讲综合，考生需学习相关知识后再研读此点）

（14）若A～Λ，则ni＝n－r（λiE－A），其中λi 是ni 重特征根.

（与第8讲综合，考生需学习相关知识后再研读此点）

（15）若A～Λ，则r（A）等于非零特征值的个数，重根按重数算.

（与第8讲综合，考生需学习相关知识后再研读此点）

证明AB行向量γi的关键依据

相关推荐