复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2025-09-30
留数的定义和计算：复变函数应用
【摘要】：若z0为函数f(z)的孤立奇点,则f(z)在z0的某个去心邻域0 ＜|z-z0|＜R内解析.由解析函数积分的闭路变形原理,对于该邻域内任意一条围绕点z0的正向简单闭曲线C,f(z) 沿C的积分取定值,下面利用该积分来定义留数.定义1 设z0(z0 ∞)为函数f(z)的孤立奇点,C为0 ＜|z-z0|＜R内围绕z0的任一条正向简单闭曲线,称积分为f(z)在点z0处的留数(Residue),记作Res
若z0为函数f(z)的孤立奇点,则f(z)在z0的某个去心邻域0 ＜|z-z0|＜R内解析.由解析函数积分的闭路变形原理,对于该邻域内任意一条围绕点z0的正向简单闭曲线C,f(z) 沿C的积分取定值,下面利用该积分来定义留数.
定义1 设z0(z0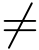 
∞)为函数f(z)的孤立奇点,C为0 ＜|z-z0|＜R内围绕z0的任一条正向简单闭曲线,称积分
为f(z)在点z0处的留数(Residue),记作Res[f(z),z0].
设函数f(z)在z0的去心邻域0 ＜|z-z0|＜R的洛朗级数为式(5.1.1),由洛朗级数的系数公式有
从而有
即f(z)在z0的留数就是f(z)在以z0为中心的圆环域内的洛朗级数中(z-z0)-1的系数.
一般情况下,用定义1来计算留数很困难,对于z0 为f(z)的可去奇点,极点或本性奇点的情形,其留数都可用式(5.2.1) 来计算,故称它为计算留数的一般公式.例如,由该式可直接推出: 若z0为f(z)的可去奇点,则它在点z0 的留数为零.
又如,当z0为f(z) = g(z-z0)的孤立奇点时,若以g(ζ)为偶函数,则f(z)在点z0的去心邻域内的洛朗级数只含ζ = z-z0的偶次幂,其奇次幂系数都为零.于是令ζ =z-z0得
由式(5.2.2)可以看出,函数
等,在奇点z = 0处的留数都为零.将这些函数的变量z换为z-z0,z0为这些新函数的孤立奇点,它们在点z0的留数也都是零.
为求函数在其孤立奇点的留数,我们只要求出它在z0的去心邻域内的洛朗级数,从而得到(z-z0)-1的系数c-1,即函数在点z0的留数.但对于有的类型的奇点,这样做是繁琐的并且也没有必要.
对于z0为极点的许多情形,用下列规则更简便
规则1° 若z0为f(z)的1级极点,则有
规则2° 若z0为f(z)的m级极点,则对任意整数n ≥m有
规则3° 设f(z) = 
其中P(z)和Q(z)在点z0 都解析.若P(z0)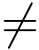 
0,Q(z0)=0 且Q′(z0)
0则z0 为f(z) 的1级极点,且有
说明 将函数的零阶导数看作它本身,规则1°可看作规则2° 当n=m=1时的特殊情形,且规则2° 可取m=1.
证明 先证规则2°,由于z0 为f(z)的m级极点,因此可设在0 ＜|z-z0|＜R内有
以(z-z0)n乘上式两端,得
由于洛朗级数在其收敛的圆环域内可以逐项求导,上式两边求n-1阶导数,由于n ≥m,则有
令z →z0取极限,得
两端再除以(n-1)!即得规则2°.(https://www.chuimin.cn)
上面证明中,取n=m=1就是规则1°的证明,下面只需证明规则3°.
由于Q(z0) = 0及Q′(z0)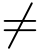 
0,因此z0 为Q(z)的1级零点,又因P(z0) 
0,故z0为f(z)= 
的1级极点.于是由上述规则1° 得在使用规则2°时,一般取n = m,这是因为n取得越大,求导的次数越多,使得计算很复杂.
例1 求下列函数在指定点处的留数.
(1) f1(z)=
,z =0及z =1;
(2) f2(z)= 
,zk =kπ(k =0,±1,±2,···).
解 (1)z =0是f1(z)的简单极点,由规则1°,得
z =1是f1(z)的2级极点,由规则2°,得
(2)zk = kπ(k = 0,±1,±2,···)是sin z 的1级零点,而cos zk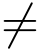 
0(k =0,±1,±2,···),由规则3°,得
若z0是f(z)的本性奇点,一般用把f(x)展开成洛朗级数的方法计算留数.
例2 求函数f(z)=
在z =0的留数.
解 z =0是f(z)的本性奇点,在圆环域0 ＜|z|＜∞的洛朗级数为
得c-1 =1,因此Res[f(z),0]=1.
若极点的级较高(3级以上),我们也往往用把函数展开成洛朗级数的方式求留数.
例3 求函数f(z)= 
在z =0的留数.
解 z = 0是函数ez -1的1级零点,又是函数z6 的六级零点.于是它是f(z)的5级极点,即m=5,可用规则2°计算其留数.
若取n=m=5,则
导数的计算比较复杂.为了计算简便应当取n=6,这时有
另外,f(z)在点z0 =0的去心邻域0 ＜|z|＜∞内的洛朗级数为
其中n=5的项的系数为
从而也有
相关文章
- 详细阅读
-
复积分在复变函数中的定义详细阅读
设C为平面上给定的一条光滑(或逐段光滑)曲线,则沿曲线C有两个方向,若选定其中的一个方向作为正方向,则称曲线C为有向曲线.设曲线C有两个端点A与B,若把从A到B的方向作为曲线C的正方向,则从B到A的方向就是C的负方向,记作C-.对于简单闭曲线,其正方向是指曲线上的点P沿此方向在该曲线前进时,邻近P点的曲线内部始终位于P点的左方,与之相反的方向就是曲线的负方向，而当曲线C为圆周时,逆时针方向就是曲线......
2025-09-30
-
泰勒定理|复变函数应用详细阅读
对于一元实函数来说,若f(x)在点x0的某邻域内有任意阶的导数,并且在该邻域内恒有余项则f(x)在点x0的该邻域内的泰勒(Taylor)级数展开式为复变函数中,函数f(x)在点z0的某邻域内有任意阶导数等价于它在该邻域内解析,对于解析函数有下面的展开定理.定理1(泰勒级数展开定理) 若函数f(z) 在圆形区域D:|z-z0| ＜R内解析,则它在D内可展开为幂级数其中 若C为D内绕z0 的正向简单闭......
2025-09-30
-
解析函数概念|复变函数及应用详细阅读
解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30
-
复变指数函数的定义及性质详细阅读
从上节例2可知,f(z)=ex(cos y+i sin y)在整个复平面上解析,且f′(z)=f(z).容易验证f(z1+z2) =f(z1)+f(z2),据此我们给出复变指数函数的定义.定义1 对任意的复数z =x+iy,定义指数函数为w =ex(cos y+i sin y),记作ez.显然,|ez|=ex ＞0,而Arg(ez)=y+2kπ(k为整数),从而ez 0.当z 取实数,即y = 0......
2025-09-30
-
复变函数应用：复数的幂与方根详细阅读
设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂，记作zn.设z =reiθ,则zn =rneinθ =rn(cos nθ+i sin nθ).当r =1时，即z =cos θ+i sin θ,有(cos θ+i sin θ)n =cos nθ+i......
2025-09-30
-
幂函数的规定及性质-复变函数及其应用详细阅读
定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定：zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2025-09-30
-
使用洛朗级数展开式计算积分-复变函数应用详细阅读
若f(z)在圆环域R1 ＜|z-z0|＜R2内解析,C 为圆环域内绕z0的正向简单闭曲线,则f(x)在该圆环域内的洛朗展开式为其中因而可以将复积分的计算转化为求被积函数的洛朗展开式中(z-z0)的负一次幂项的系数c-1.例4 计算积分解 函数f(z)= 在1 ＜|z|＜∞内解析,|z|=3 在此圆环域内,把它在此圆环域内展开得故从而例5 计算积分解 先分析函数的解析性.令ζ = 由于ln ζ的不解......
2025-09-30
相关推荐