首页理论教育复变函数导数及应用-复变函数及其应用

复变函数导数及应用-复变函数及其应用

2023-10-30 理论教育版权反馈

【摘要】：复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内

复变函数导数的定义在形式上与一元实变函数一致.

定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限

存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作

若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有

若函数w =f(z)在区域D内处处可导,则称f(z)在D内可导.

例1 证明函数f(z)=|z|2除去在z =0 外,处处不可导.

证明当z0 =0时,

即f(z)在z =0可导.

但当z0 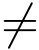pagenumber_ebook=39,pagenumber_book=30 0时是不可导的,证明如下：

设z0 =x0+iy0,若取z =x+iy0,则

若取z =x0+iy,则

由于x0,y0不能同时为0,所以当z分别沿平行于x轴和y轴的两个方向趋于z0 时,趋于不同的极限值,所以f(z)在z pagenumber_ebook=39,pagenumber_book=30 0不可导.

例2 若函数w =f(z)在z0可导,试证f(z)在z0点连续.

证明由于

所以f(z)在z0点连续.

由例2易知函数可导与连续性的关系: 若函数w = f(z) 在点z0处可导,则w = f(z)在点z0处必连续.但函数在一点连续,未必在该点可导.在复变函数中,容易举出处处连续但处处不可导的例子,而在实变函数中举出这种例子是不容易的.

例3 函数f(z) = Rez 在整个复平面内处处都是连续的,但在任何一点均不可导.

解设z =x+yi,△z =△x+i△y,则f(z)=Rez =x.显然f(z)是整个复平面上的连续函数.

另一方面,(www.chuimin.cn)

当△z →0时,上式极限不存在.因为当△z =△x+i0 →0 时,上式极限为1;当△z =0+i△y →0 时,上式极限为0.由此知函数f(z)=Rez处处不可导.

例4 试证: f(z)=zn(n为正整数)在z 平面上处处可导,且

证明设z是z平面内任意固定的点,于是

由于复变函数中导数的定义和极限运算法则与一元实变函数完全相同,所以实变函数中求导法则完全可以推广到复变函数中来,且证法相同.这些求导法则如下:

(1) (c)′ =0,其中c为任意复常数;

(2) (zn)′ =nzn-1,其中n为正整数;

(3) [f(z)±g(z)]′ =f′(z)±g′(z);

(4) [f(z)g(z)]′ =f′(z)g(z)+f(z)g′(z);

(5)

(6) [f(g(z))]′ =f′(w)g′(z)，其中w =g(z);

(7) [f(z)]′ =,其中w = f(z) 与z = φ(w)是两个互为反函数的单值函数,且φ′(w) pagenumber_ebook=40,pagenumber_book=31 0.

复变函数的微分概念在形式上与一元实变函数的微分完全一样.

若函数w =f(z)在点z0可导,由导数的定义知

△w =f(z0+△z)-f(z0)=f′(z0)△z+ρ(△z)△z,

其中,f′(z0)△z是函数改变量△w的线性主部,因此|ρ(△z)△z|是|△z|的高阶无穷小量.于是我们称f′(z0)△z为函数w = f(z) 在点z0 处的微分,记作

若函数在点z0处的微分存在,称函数f(z)在点z0处可微.

若函数w =f(z)在区域D内处处可微,则称f(z)在D内可微.特别地,函数f(z)在点z0 处可导与可微是等价的.