我们如果只凭直观感受进行判断,那么很可能产生错觉或错误的判断,我们把看上去的情况和实际有偏差的图形,称之为错视图形．知能概述面积是平面几何中一个重要概念,计算图形面积是平面几何中最基本的问题之一,常用的计算方法有:和差法、运动法、等积变形法．面积的计算主要是求一些非常规图形的面积,非常规图形面积的计算往往可转化为常规图形面积的计算．在转化的过程中,常用到恰当连线、图形割补、等积变形、线段比与面积比......
2023-08-13
面积坐标系与坐标的引入、性质及应用
【摘要】：有了带号面积，就可以引入面积坐标了。在式中，若S＞0，便称为右手坐标系，S＜0称为左手系。这时，便叫做M＝的齐次面积坐标。这样，面积坐标实际上包括了重心坐标、仿射坐标、直角坐标等多种坐标。在面积坐标系里推出一个公式来，马上可以变换成在其他坐标系里的公式。从式中消去参数λ，得这就是M、M1、M2三点共线的条件，也可以看成M的面积坐标所满足的直线方程式。这就是面积坐标系或重心坐标系里直线方程式的一般形式。
从小学到初中，面积都是正的；但如果引入带正负号的面积，有时更为方便。
按照通常的约定，简单多边形（即边界不和自己相交的多边形）面积，依照边界“走向”来确定正负号。如果指定的边界走向是逆时针方向，面积为正；反之，边界走向为顺时针方向，面积为负。至于边界走向，可以在图上用箭头表示，也可以用顶点的排列顺序表明（如图6-6）。
为了区分带号面积与不带号面积，我们在表示面积的符号上画一横线来表示带号面积，如
等等。
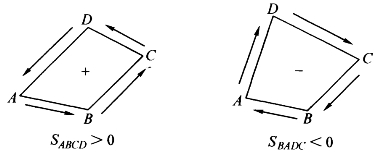
图6-6
带号面积的好处，在于它可以用更简洁的语言来描述一些几何事实。例如，下面的三句话说的是平凡的几何事实：
（1）若P在线段BC上，则
△ABC＝△ABP+△APC。
（2）若P在BC的延长线上，则
△ABC＝△ABP－△APC。
（3）若P在CB的延长线上，则
△ABC＝△APC－△ABP。
这么平常的事，要啰嗦好几句。如果用了带号面积，三句话便可以并成一句：若P在直线BC上，则
图6-7清楚地表明了上面这个等式的含意。
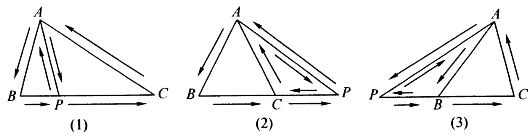
图6-7
注意，当P在BC边上时，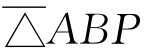
与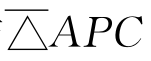
同号，（6.2.1）式成为△ABC＝△ABP+△APC，即（1）。若P在BC的延长线上时，
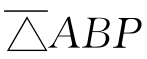与
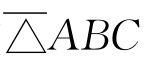同号但与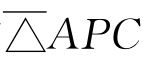
反号，（6.2.1）式成为△ABC＝△ABP－△APC，成了（2）。当P在CB的延长线上时，
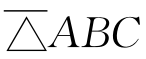与
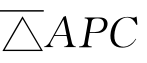同号而与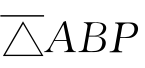
反号，它又成了（3）。你看，一个简单的等式就这样包含了丰富的信息。
再看图6-8。（1）表示凸四边形的面积为两个三角形面积之和，（2）表示凹四边形面积等于两个三角形面积之差。即：
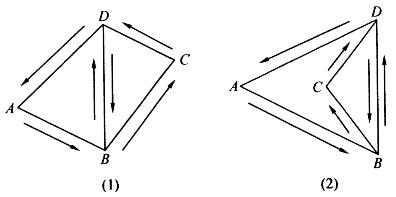
图6-8
（1）S凸四边形ABCD＝△ABD+△BCD，
（2）S凹四边形ABCD＝△ABD－△BCD。
用了带号面积，这两个等式便可以统一叙述成
类似地，可以引进“有向角”的概念。我们约定：若
＞0，则∠ABC为正角，反之为负角。用记号
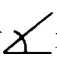表示有向角，则三角形的带号面积公式是
而带号面积的共边比例定理，则可以配合有向线段表示为
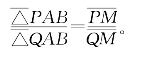
张角公式可以用有向角表示为
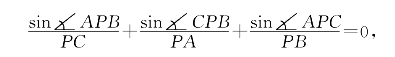
或者写成
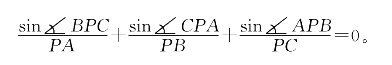
这样使用了带号面积、有向角和有向线段之后，可以使许多命题表述得更一般，证起来更简单，用起来更广泛。限于篇幅，这里不再详述。
有了带号面积，就可以引入面积坐标了。
规定了顶点排列顺序的三角形叫定向三角形，定向三角形ABC记作
。在平面上任取一个定向三角形
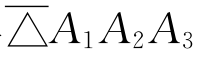，叫它“坐标三角形”，A1、A2、A3叫做基点。对平面上任一点M，就有了3个三角形：
、
、
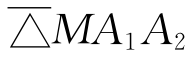。这3个三角形的带号面积分别记作
图6-9
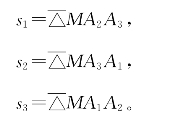
它们的定向，由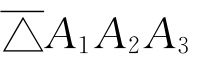
中三边的走向决定（如图6-9）。
我们把三元数组（s1，s2，s3）叫做（以
为坐标三角形时）点M的“面积坐标”，记作
M＝（s1，s2，s3）。
显然，相同的点有相同的坐标，不同的点有不同的坐标。s1、s2、s3叫做M的三个“坐标分量”。
不过，随便给三个数，可不一定是某个点的坐标。因为如果记S＝
，一个点的坐标（s1，s2，s3）一定要满足
仔细看一看图6-9，便可“看”出这条规律来。
在（6.2.2）式中，若S＞0，便称为右手坐标系，S＜0称为左手系。当不加说明时，通常指右手系。
既然一个点的三个坐标分量之间满足关系s1+s2+s3＝S，那么，只要知道了两个，便可以写出第三个来。例如当S＝8时，一个点的坐标是（a，b，*），这*一定是8－a－b，而（3，*，－1）便是（3，6，－1），（*，π，3）便是（5－π，π，3），等等。
确定一个点的面积坐标还有另外一种途径，即给出三者之比
s1∶s2∶s3＝μ1∶μ2∶μ3。(www.chuimin.cn)
这时，（μ1∶μ2∶μ3）便叫做M＝（s1，s2，s3）的齐次面积坐标。通常，也把（μ1∶μ2∶μ3）叫做M的重心坐标。其物理意义是鲜明的：如果给A1、A2、A3赋以质量μ1、μ2、μ3，则质点A1（λ1）、A2（μ2）、A3（μ3）的重心恰在M处。
重心坐标与面积坐标之间的换算很简单。若M的面积坐标是（s1，s2，*），则任取一实数k≠0，便得到M的一组重心坐标（ks1∶ks2∶k（s－s1－s2））；反过来，若M的重心坐标为（μ1∶μ2∶μ3），则其面积坐标为
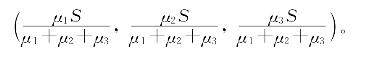
由此看出，一个点的重心坐标（μ1∶μ2∶μ3）应当满足条件μ1+μ2+μ3≠0（若μ1+μ2+μ3＝0，就说（μ1∶μ2∶μ3）代表一个“无穷远点”）。当μ1+μ2+μ3＝1时，（μ1∶μ2∶μ3）叫做“规范重心坐标”。当S＝1时，面积坐标也就是规范重心坐标。
既然知道了M＝（s1，s2，s3）的两个面积坐标分量就可以确定M，所以可以干脆用（s1，s2）来表示点M，或者用
来表示。这时，
叫做在坐标系
之下M的仿射坐标，而A3叫做这个仿射坐标系的原点。
如果
，且∠A1A3A2＝90°，则这个仿射坐标系{A3，
}叫做笛卡儿坐标系，也就是常用的直角坐标系。
这样，面积坐标实际上包括了重心坐标、仿射坐标、直角坐标等多种坐标。在面积坐标系里推出一个公式来，马上可以变换成在其他坐标系里的公式。
下面列出面积坐标系里的几个基本公式
（1）定比分点公式
在面积坐标系里M1＝（s1，s2，s3），M2＝（t1，t2，t3），而M在直线
M1M2上，且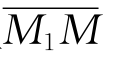
∶
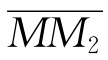＝λ，则M的坐标（x1，x2，x3）可用下列公式计算：
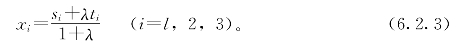
这一公式的证明，可参照例5.3.8的证明。根据这个公式，可写出仿射坐标系、直角坐标系以及规范重心坐标系里的类似公式。但是，这个公式在一般重心坐标系里并不成立。因为每个点的坐标可乘以任意因子，这破坏了定比组合的性质。
（2）直线方程式
设直线l上有两个点M1（s1，s2，s3）、M2（t1，t2，t3），则l上任一点M（x1，x2，x3）应满足条件（6.2.3）式，即这里参数λ＝
。从（6.2.4）式中消去参数λ，得
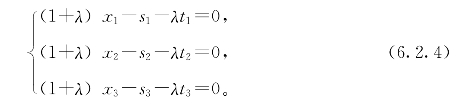
这就是M、M1、M2三点共线的条件，也可以看成M的面积坐标所满足的直线方程式。
把上面这个行列式的第一、二行加到第三行上，并且把第三行除以S，得
这就是仿射坐标系里三点共线的条件，或者说是仿射坐标系里的直线方程式。
把（6.2.5）式展开，得
c1x1+c2x2+c3x3＝0。
这就是面积坐标系或重心坐标系里直线方程式的一般形式。
那么，系数c1、c2、c3有什么几何意义呢？回答颇为有趣。设A1、A2、A3到直线l的带号距离分别为h1、h2、h3，并约定若Ai、Aj位于l的同侧，则hi、hj同号，否则hi、hj反号。这时一定有
图6-10
事实上，如图6-10，设直线l交A1A2于P，则P的面积坐标为（s1，s2，0）。因P在l上，故
c1s1+c2s2＝0。
又设A1、A2到l的垂足分别为Q1、Q2，则
同理c2∶c3＝h2∶h3，于是（6.2.6）式成立。
（3）两点距离公式
如图6-11，求两点M＝（s1，s2，s3）、N＝（t1，t2，t3）的距离。作NP∥A2A3，并使MP∥A1A3，记
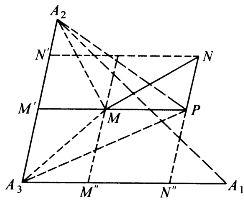
图6-11
易求出
由余弦定理得
这个公式关于3个坐标分量不对称。若S：1，并记
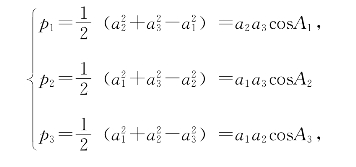
则可以验证
这个公式有简洁而对称的形式。如果取△A1A2A3为正三角形，且a1＝a2＝a3＝
，则p1＝p2＝p3＝1。注意，p1、p2、p3正是本章第5小节将引入的勾股差之半。
关于面积坐标在解题时的大量应用，有兴趣的读者可参看《初等数学论丛》（3）中杨路的文章《谈谈重心坐标》。
有关从数学教育到教育数学的文章
- 详细阅读
-
高等数学：曲面积分的概念与性质详细阅读
在本章第一节的质量问题中，如果把曲线改为曲面，并相应地把线密度ρ（x，y）改为面密度ρ（x，y，z），小段曲线的弧长Δsi改为小块曲面的面积ΔSi，而第i小段上面的一点（ξi，ηi）改为第i小块曲面上的一点（ξi，ηi，ζi），那么在面密度为ρ（x，y，z）连续的前提下，所求的质量M就是下列和的极限：其中λ表示n小块曲面的直径的最大值.抽去它们的具体意义，就得出对面积的曲面积分的概念.定义1 设曲......
2023-10-19
-
用户坐标系图标的优化显示技巧详细阅读
UCS图标可以帮助用户使用户坐标系的当前方向可视化。用户也可以切换至“三维建模”工作空间在功能区“常用”选项卡的“坐标”面板中单击“UCS图标，特性”按钮来打开“UCS图标”对话框以控制UCS图标的样式、大小和颜色。图9-2 “UCS图标”对话框AutoCAD中的UCS图标可以显示有图9-3所示的3种版本。“在原点处显示UCS图标”按钮用于仅在原点处显示UCS图标；“显示UCS图标”按钮用于在原点或视口角点处显示UCS图标；“隐藏UCS图标”按钮用于隐藏UCS图标。......
2023-06-20
-
物理性质指标的换算方法详细阅读
换算指标可以通过三相图由实测指标换算求得。具体方法是：首先绘制三相图，然后根据情况令V=1g/cm3，再根据三个实测指标的定义式进行计算，把三相图左侧质量和右侧体积一共8个未知量逐个计算出来并填入草图，由此即可求得所需要的各个指标。图1.5三相组成计算图由Va=Vv-Vw可得Va=0.435-0.275=0.16。由此，三相图中各部分都已算出。表1.1土的物理性质指标常用换算公式续表......
2023-08-28
-
非线性算子的性质及应用详细阅读
非线性算子的性质包括连续性、有界性、全连续性、可微性等.这是一些基本概念和性质,在后面各章中都要用到.设E1和E2时两个实Banach 空间,D E1.设A∶D→E2为非线性的.定义1设x0∈D.若ε>0,δ=δ(x0,ε)>0 使得当x ∈D且‖x-x0‖ < δ 时,恒有‖Ax -Ax0‖ < ε,则称A 在x0连续;若A 在D 中每一点都连续,则称A 在D 上连续;若上述δ 只与ε 有关而......
2023-10-20
-
正弦函数性质及解析-机电应用数学详细阅读
由正弦函数y=sinx的图像可知：定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx，x∈R的值域是[-1，1]，即对任意的x∈R，都有-1≤sinx≤1.其中，当，k∈Z，有ymax=1；当，k∈Z时，有ymin=-1.想一想等式2sinx=3，，都成立吗？例2求出下列函数的最大值和最小值：y=1-sinx； y=2sinx.解：当sinx=-1时，ymax=1-（-1）=2；当sinx=1时，ymin=1-1=0.当sinx=1时，ymax=2×1=2；sinx=-1时，ymin=2×（-1）=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时，对应的x的取值集合分别是什么？......
2023-11-22
-
不同染料的性质与应用详细阅读
由此可见，染料实际上是一种有选择性地反射一定波长光线的物质。溶解碱性染料不宜用硬水和带碱性的水，否则会产生色斑，通常加入1%的稀醋酸，用70℃以下的热水溶解后使用。碱性染料对木素的亲和力极大，所以对未漂浆和机木浆容易染色。图2-25 盐基槐黄（二）酸性染料酸性染料为盐类，一般都含有磺酸基、羧基和羟基等可溶性基团，易溶于水，溶液呈酸性，且多在酸性介质中染色，故称酸性染料。......
2023-06-23
-
WGS-84坐标系简介及应用详细阅读
GPS输出的位置数据就是这个坐标系下的数据。上面这句话复杂一点解释就是：GPS单点定位的坐标以及相对定位中解算的基线向量属于WGS-84大地坐标系。一句话理解：把ECEF用在GPS中就是WGS-84坐标系。因为GPS输出的信息是相对于WGS-84坐标系，我们可以把它看作一个参考椭球体，GPS输出的高度是垂直于椭球表面的高度，不是相对于海平面的高度。......
2023-07-05
相关推荐