首页理论教育综合题的分析与作图-《画法几何及土木工程制图》

综合题的分析与作图-《画法几何及土木工程制图》

2023-09-24 理论教育版权反馈

【摘要】：图3—27求作符合条件的直线解空间分析：过M点与△ABC平行的直线有无数条，其轨迹是与△ABC平行的平面，由此可先作出这个与△ABC平行的轨迹平面P，然后作出平面P与直线DE的交点N，M和N的连线即为所求。

前面讨论了点、直线、平面的投影规律及它们的相对位置，并介绍了若干基本的作图方法，这样就可以来图解空间的几何问题了。这类问题往往是综合性的，要灵活运用几何原理和投影规律进行空间分析，根据已知条件和所求问题，想象出各几何元素的空间关系，寻找解题的途径，确定解题的步骤，然后利用已掌握的作图方法，逐步完成解答。

例3—9　如图3—27a，试过M点作直线MN，使其与△ABC平行，且与直线DE相交。

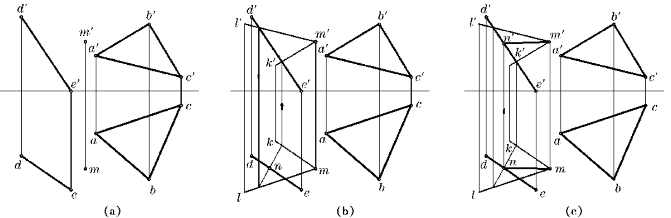
pagenumber_ebook=48,pagenumber_book=36

图3—27　求作符合条件的直线

解　空间分析：过M点与△ABC平行的直线有无数条，其轨迹是与△ABC平行的平面，由此可先作出这个与△ABC平行的轨迹平面P，然后作出平面P与直线DE的交点N，M和N的连线即为所求。

作图步骤如图3—27b，c所示：

（1）作MK∥AB，即mk∥ab，m′k′∥a′b′，再作ML∥AC，即ml∥ac，m′l′∥a′c′，于是平面P[MK×ML]∥△ABC；

（2）求出DE与平面P的交点N[n，n′]；

（3）连接M和N，则MN与DE相交，且MN∥△ABC。

例3—10　如图3—28a所示，求A点到直线MN的距离。

解　空间分析：要求点到直线的距离，首先过该点作已知直线的垂线，该点与垂足之间线段的实长即为所求。由于空间两条互相垂直的一般线，其投影都不反映垂直，所以要求得A点到MN的距离，应先包含A点作一平面Q垂直于MN，然后作出它们的交点K，AK即为垂线，最后求出AK的实长，就得到A点到直线MN的距离。

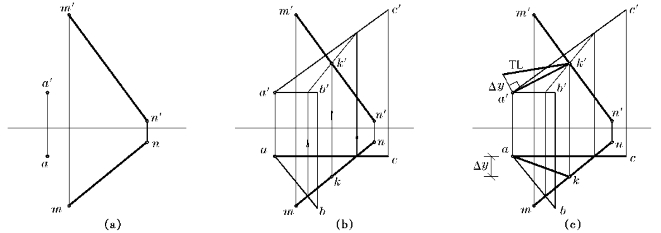
pagenumber_ebook=48,pagenumber_book=36

图3—28　求点到直线的距离

作图步骤如图3—28b，c所示：

（1）过A点作水平线AB⊥MN，即a′b′∥OX，ab⊥mn；过A作正平线AC⊥MN，即ac∥OX，a′c′⊥m′n′，于是所作平面Q[AB×AC]⊥MN；

（2）求出Q与MN的交点K[k，k′]，连线AK⊥MN；

（3）用直角三角形法作出AK的实长，即为所求距离。