当流体渗流服从达西定律时,通过某截面的流量与水力梯度成过原点的直线关系;当流量和水力梯度关系不能用直线关系表示时,这样的渗流过程就是非达西渗流过程,或称非线性渗流。由此得出结论,在Re<5范围内达西定律是适用的。如图1.11所示,渗透性与压力关系可用下式表述此时,一维渗流情形下达西定律可写为因为流体没有密切接触固体壁面,所以低压气体分子在固体壁面上可以具有一定的非零速度。......
2023-06-28
1.3.2.1 达西定律
地下水的运动有层流、紊流和混合流三种形式。层流是地下水在岩土的孔隙或微裂隙介质中渗透,产生连续水流;紊流是地下水在岩土的裂隙或洞穴中流动,具有涡流性质,各流线有互相交错现象;混合流是层流和紊流同时出现的流动形式。
当地下水在土中的运动(渗透)属于层流时(图1-16),且遵循达西(Darcy)线性渗透定律,其公式如下:
![]()
式中 Q——单位时间内的渗透水量,m3/d;
K——渗透系数,m/d;
A——水渗流的断面积,m2;
L——断面间的距离,m;
h——距离为L的断面间的水位差,m,h=H1-H2;
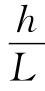 ——水力坡度,用符号I表示,代表单位长度渗流途径上所产生的水头损失,亦称水力梯度(无因次)。
——水力坡度,用符号I表示,代表单位长度渗流途径上所产生的水头损失,亦称水力梯度(无因次)。

达西公式两边用断面积A除后,即得渗流速度(v),渗流速度与水力坡度成正比:

当I=1时,得K=v,即当水力坡度等于1时,渗透系数等于渗流速度,它的单位为cm/s或m/d。
由式(1-13)可见,土体的渗透系数K也就是水力坡度等于1时的渗流速度。水在土体中的渗流速度v取决于两方面的因素:一是土体的透水性(反映为K的大小);二是水力条件(反映为I的大小),这就是水在土体中渗流的基本规律,亦即达西定律。
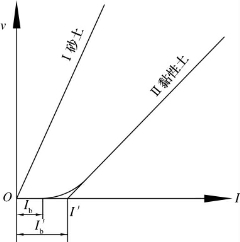
图1-17 砂土与黏性土渗流速度与水力坡度的试验关系
这里要注意两个问题:
(1)v并不是水在土体孔隙中真正流动的速度,因为孔隙是弯弯曲曲的,实际渗流途径并不等于L;横截面积A中不全是孔隙,实际过水面积不等于A。因此,实际平均流速大于渗流速度v。但工程实践中关心的不是水质点的真正流速,而是流经整个土体的平均流量。所以用表观的流速v,同时按表观的A、L考虑是可以的,而且更为方便。
(2)达西定律v=KI只适用于砂及其他较细颗粒中。因为,孔隙太大时(如卵石、溶洞),流速太大,会有紊流现象,水质点的流线互相交错,不是层流,v不再与I的一次方成正比。渗流速度不是孔隙中的实际流速(u),它只是换算速度,因为在这个公式中用的断面积并不是孔隙的横断面积。
为了得到地下水在土体孔隙中运动的平均实际流速,可用流量Q除以孔隙所占的面积A′,故地下水的平均实际流速为

式中,n为土体的孔隙率,%。
将式(1-12)代入式(1-14)中,即得地下水的平均实际流速
![]()
因为n永远小于1,可见平均实际流速大于渗流速度。
水在砂土中流动时,达西公式是正确的,如试验所得图1-17中的曲线I所示。但是,在某些黏性土中,这个公式就不正确。因为,在黏性土中颗粒表面有不可忽视的结合水膜,阻塞或部分阻塞了孔隙间的通道。试验表明,I值比较小时克服不了结合水膜的阻力,水渗流不过去,只有当水力坡度I大于某一值Ib时,黏土才具有透水性(见图1-17中的曲线Ⅱ)。如果将曲线Ⅱ在横坐标上的截距用I′b表示(称为起始水力坡度),当I>I′b时,达西公式可改写为
v=K(I-I′b) (1-16)
1.3.2.2 达西定律的适用范围
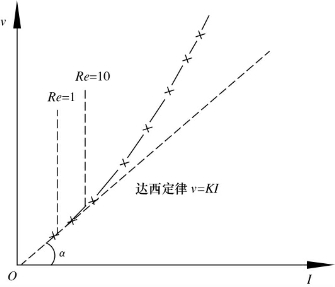
图1-18 渗透速度与水力坡度的关系
达西定律并非任何渗流皆适用,而是有一定的适应范围。较早以前,认为达西定律的适用条件是层流,故有时把它称为层流渗透定律。20世纪40年代以来,很多实验证明并非所有地下水的层流运动都符合达西定律,确实有不符合达西定律的地下水层流运动。雅各布·贝尔通过试验得出渗流速度和水力坡度的关系曲线(图1-18)。由图可见,当雷诺数(Re)小于10时,该曲线基本上呈直线,即此时地下水的运动服从达西定律。当雷诺数(Re)大于10以后的曲线便偏离直线但仍属层流运动,这是一种非线性层流运动。向上逐渐过渡到紊流。有人提出将雷诺数等于10作为层流的上限。
雷诺数由下式求得:

式中 ρ——流体密度;
v——流体流速;
D——流体通过的横截面直径;
μ——流体的动力黏滞系数。
很多人用惯性力的影响解释上述现象。即当地下水运动速度慢时,黏滞性所产生的摩擦力对运动的影响占绝对优势,惯性力的影响可以忽略不计,水流服从达西定律;当地下水的运动速度加快,水流具有明显的连续变化的速度和加速度,惯性力与速度平方成正比,达西定律就不适用了。这一变化发生于水流由层流转变为紊流之前。
由于含水层中空隙的大小、形状和方向都在很大范围内变化,有些空隙中的水流转变了,另一些空隙中的水流则没有转变,因此由服从达西定律的层流运动到非线性层流运动再到紊流运动是逐渐过渡的,无明显界线。在自然情况下,绝大多数的地下水流是服从达西定律的。
1.3.2.3 水力坡度
水力坡度为沿渗透途径水头损失与相应渗透长度的比值。水质点与颗粒在空隙中运动时,为了克服水质点之间的摩擦阻力,必须消耗机械能,从而出现水头损失。所以,水力坡度可以理解为水流通过单位长度渗透途径为克服摩擦阻力所耗失的机械能。
1.3.2.4 渗透系数
渗透系数K反映土的透水性大小,其常用量纲为cm/s或m/d,一般通过做室内渗透试验或现场抽水或压水试验进行测定。
1.影响土的渗透系数的主要因素
(1)土的粒度组成。一般土粒愈粗、大小愈均匀、形状愈圆滑,K值也就愈大。对于洁净的(不含细粒土的)砂土,可按下列经验公式估计K(cm/s)值:
K=100~150(d10)2 (1-18)
式中,d10为土的有效粒径,亦即土中小于此粒径的土重占全部土重的10%,mm。粗粒土中含有细粒土时,随细粒含量的增加,K值急剧下降。
(2)土的密实度。土愈密实,K值愈小。试验资料表明,对于砂土,K值大致上与土的孔隙比e的二次方成正比;对于黏性土,孔隙比e对K的影响更大,但由于涉及结合水膜的厚薄而难以建立二者之间的经验关系。
(3)土的饱和度。一般情况下饱和度愈高,K值愈大。这是因为土的孔隙中气泡的存在会减小过水截面积,甚至堵塞细小孔道。
(4)土的结构。细粒土在天然状态下具有复杂结构,结构一旦扰动,原有的过水通道的形状、大小及其分布就会改变,因而K值也就不同。扰动土样与击实土样的K值通常都比同一密度原状土样的K值要小。
(5)土的构造。土的构造因素对K值的影响也很大。例如,在黏性土层中有很薄的砂土夹层的层理构造,会使土在水平方向的K值比垂直方向的K值大许多倍,甚至几十倍。因此,在室内做渗透试验时,土样的代表性很重要。另外,所测得的K值也只能代表天然土层中一个点的渗透系数,不一定能代表整个土层的透水性。有条件时,通过现场抽水试验或压水试验来测定天然土层的K值较为可靠。
(6)水的温度。试验表明,渗透系数K与渗流液体(水)的重度γw以及黏滞系数η(Pa·s)有关。水温不同时,γw相差不多,但η变化较大。水温愈高,η愈低,K愈大,K与η基本上呈线性关系。因此,在T℃测得的KT值应加温度修正,使其成为标准温度(10℃)下的渗透系数K10值

式中,ηT,η10分别为T℃,10℃时水的黏滞系数(可查物理手册)。对于T为5℃时的情况 =1.161;对于T为20℃时的情况
=1.161;对于T为20℃时的情况 =0.773。由此可见,水温因素的影响不容忽视。
=0.773。由此可见,水温因素的影响不容忽视。
地下水的温度一般在10℃左右,故采用10℃作为标准温度,有的国家以15℃或20℃作为标准温度。
2.渗透系数的测定
渗透系数测定的试验装置如图1-19和图1-20所示,有定水头和变水头两种。室内渗透试验的原理如图1-8所示,量测Q后反算K。
[实验1]定水头渗透仪如图1-19所示。已知渗透仪直径D=75mm;在L=200mm渗流途径上的水头损失h=83mm,在60s时间内的流量Q=71.6cm3;求土的渗透系数。
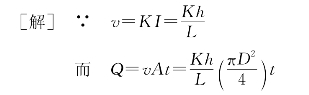
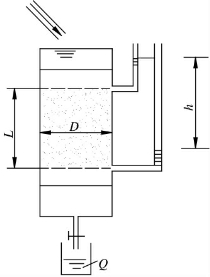
图1-19 定水头
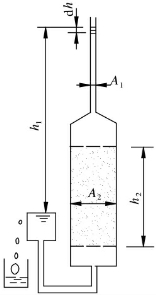
图1-20 变水头
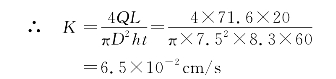
[实验2]变水头渗透仪如图1-20所示。已知A1=1.77cm2,A2=44.18cm2,L=15cm,h1=130cm,h2=80cm,t2-t1=135s;求土的渗透系数。
[解]设dt时间内,储水管的水面下降dh,则
(1)从储水管流出的水量为dV=A1dh
(2)此水量必等于同一时间内流经土样的流量为
![]()
(3)由于dV=dQ,则
![]()
当时间从t1变化到t2时,储水管水面从h1降至h2,可写成
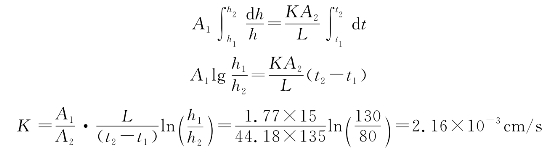
3.渗透系数经验值
表1-4可用于粗略估算土的渗透系数。
表1-4 各类土的渗透系数

有关工程地下水(第2版)的文章

当流体渗流服从达西定律时,通过某截面的流量与水力梯度成过原点的直线关系;当流量和水力梯度关系不能用直线关系表示时,这样的渗流过程就是非达西渗流过程,或称非线性渗流。由此得出结论,在Re<5范围内达西定律是适用的。如图1.11所示,渗透性与压力关系可用下式表述此时,一维渗流情形下达西定律可写为因为流体没有密切接触固体壁面,所以低压气体分子在固体壁面上可以具有一定的非零速度。......
2023-06-28

达西定律试验的装置见图1.5。3.达西定律类比渗流力学中的达西定律和热传导中的傅里叶传热定律、电学中的电流定律极其类似,以流量表达式为例式中:QT为热量;kT导热系数;T为温度;QE为电流强度;ρE为电阻率;E为电压;L为传导距离。......
2023-06-28

在渗流工程中,多孔介质表面作用明显,流体流动过程中任何时候必须考虑黏性的作用;地下渗流中通常具有较高的压力,压力变化亦比较明显,需要考虑流体和介质的压缩性;孔道结构复杂,有时需要考虑毛管力的作用;某些情况下还需要考虑吸附、解吸、弥散等物理化学作用。研究流体渗流过程的方法有流体力学方法、水动力学方法和实验方法。......
2023-06-28

此外,地下水流速的测定,尚可用人工放射性同位素单井稀释法于现场测定。地下水实际流速测定方法参考表2-9。图2-21单井法试验表2-9地下水实际流速测定方法......
2023-09-23

变密度地下水渗流与溶质运移的模拟研究主要集中在井的升锥问题、滨海地区海水入侵问题、污染废物的处置问题以及大密度污染物的迁移等。Graf and Simmons将变密度地下水流溶质运移模型用于模拟裂隙岩石中地下水溶质迁移过程,这也是变密度模型的新研究热点之一。滨海地区变密度地下水流溶质运移模型与分布式水文模型耦合模拟海水入侵趋势是一种很必要的尝试,也会是未来研究发展的主体方向。......
2023-06-25

图2-46试验场地抽水井和观测井平面布置抽水试验现场工作要求:①各班人员必须严格职责,不得擅自离开岗位,需按时精确量测水位和水量。绘制抽水试验综合成果图。应用稳定流法和非稳定流法求含水层水文地质参数。表2-30含水层水文地质参数汇总......
2023-09-23

通过进一步的分析可知,各层纵向纤维的线应变沿截面高度应为线性变化规律,从而由虎克定律可推出,梁弯曲时横截面上的正应力沿截面高度呈线性分布规律变化,如图7-2所示。图7-1梁的弯曲应力图7-2梁弯曲时,正应力分布规律......
2023-06-16
相关推荐