特别需要指出的是:在相似条件下,两个通风机的比转数是相等的。当进口状态是非标准或气体种类不同时,比转数的计算要考虑气体密度的变化。标准状态气体的密度为1.2kg/m3则比转数为比转数可以用量纲一的参数、来表示:对于标准进口状态,ρ=1.2kg/m3,则比转数为在离心通风机中,有时采用双面进气形式,以扩大流量范围。轴流通风机采用双级形式,以提高升压,而一般的比转数公式是按单级单面进气计算的。......
2023-08-20
(1)离心通风机叶轮的结构 离心通风机的叶轮主要由叶片、前盘、后盘、轮盘等部件组成。其中,除轮盘用铸铁或铸钢制成外,其他部件一般都是由钢板制成。叶片有平板、圆弧、中空机翼型等形状;前盘有平的、圆锥的、圆弧的等形状;后盘则是平的圆盘。
前、后盘与叶片的连接一般采用焊接,或者由铆钉铆接。后盘与轮盘连接一般都采用铆钉铆接。图7-24为各种不同结构形式叶轮简图。
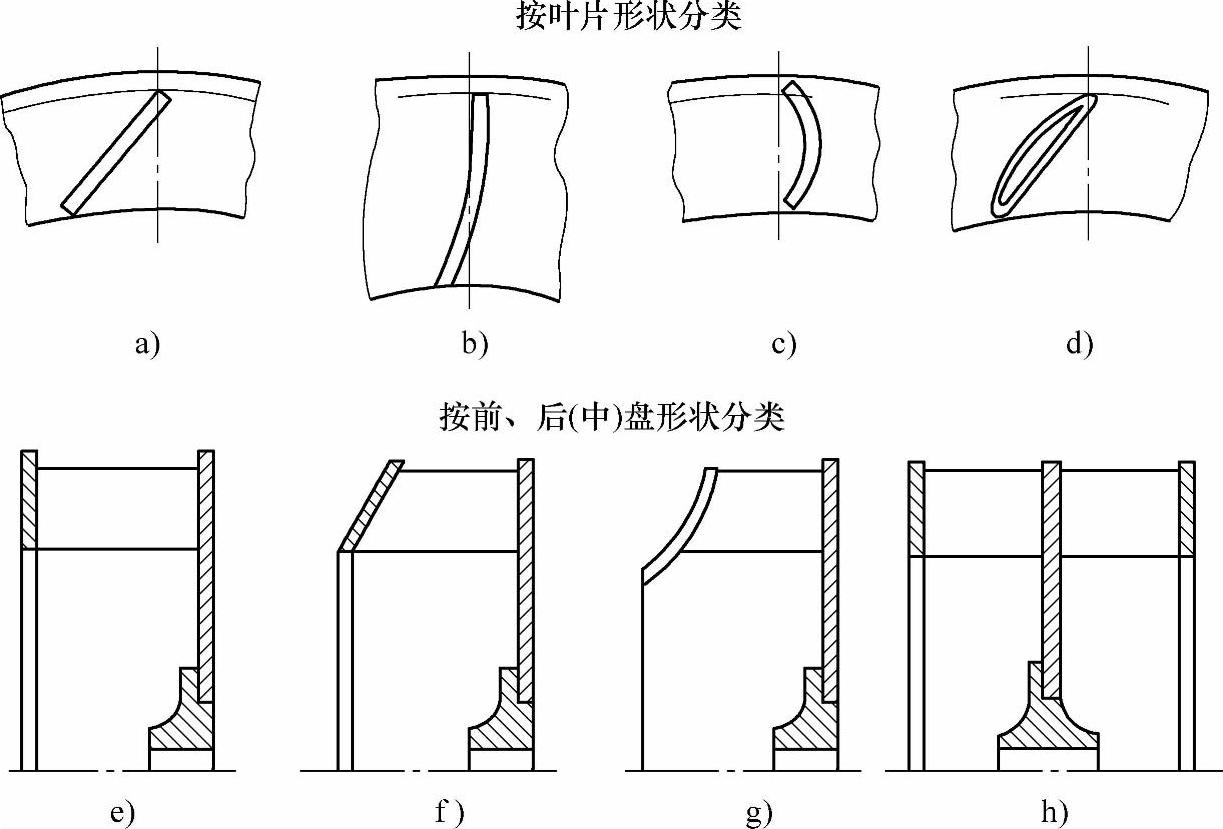
图7-24 各种不同结构形式叶轮简图
a)平板叶片 b)圆弧窄叶片 c)圆弧宽叶片 d)中空(机翼型)叶片 e)平行盘叶轮 f)圆锥前盘叶轮 g)圆弧前盘叶轮 h)具有中盘的叶轮
(2)轮盘强度的计算 轮盘旋转时产生离心力,在该力作用下使轮盘截面产生拉伸应力。如果最大拉伸应力超过材料的许用值[σ],则轮盘被拉断,不能工作,造成事故。为了保证轮盘工作安全可靠,应校核其安全强度,即计算出轮盘危险截面处的最大拉伸应力σmax(Pa),使其满足
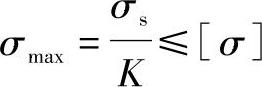
式中,σs为材料的屈服极限(Pa);K为安全系数,取K≥2。

图7-25 等厚薄圆环以角速度ω绕轴旋转
1)轮盘形状和尺寸对应力的影响:
①等厚薄圆环的旋转应力。图7-25示出等厚薄圆环以角速度ω绕轴旋转。现在研究由于离心力作用下引起的应力。在薄圆环上取一微元体,其两个子午面夹角为dα,截面面积为A=bδ,平均直径为d,微元体质量为 。旋转的微元体上作用力有:
。旋转的微元体上作用力有:
作用在截面上的切向力由下式计算:
FT=σtbδ离心力为

由图7-25中的力三角形表示这些力的平衡,
则
F=FTdα
或
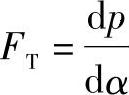 则 σtpu2 (7-39)式中σt为薄圆环的离心拉伸应力(Pa);u为薄圆环平均直径处的圆周速度(m/s);ρ为材料的密度(kg/m3)。
则 σtpu2 (7-39)式中σt为薄圆环的离心拉伸应力(Pa);u为薄圆环平均直径处的圆周速度(m/s);ρ为材料的密度(kg/m3)。
由式(7-39)可见,等厚薄圆环的旋转应力与材料密度成正比,与圆环的平均直径处的圆周速度平方成正比。
②圆环径向尺寸对应力的影响。图7-26示出两个外径相同、内径不同的圆环,各以相同的转n旋转。这两个圆环中的应力将是不同的。从式(7-39)可知:平均直径D大,其平均直径处的圆周速度也大,则应力σt也就大。同理,当外径D2相同时,若内径D1大,则平均直径D大,应力σt也大。反之,内径D1小,则平均直径D小,应力σt也就小。
将D1与D2的比值称为镗孔度ε。当镗孔度ε大,则应力σt大。所以要尽可能减少镗孔度ε。对大圆环应特别注意减少镗孔度ε,以降低应力。
③圆环轴向尺寸对应力的影响。图7-27示出三种不同轴向尺寸的圆环。其中,内径处的厚度b1都相同。对于锥形和双曲线圆环,其外径处的厚度b2′也相同。设在同一转速下,分析哪种圆环应力大?

图7-26 两个外径相同、内径不同的圆环
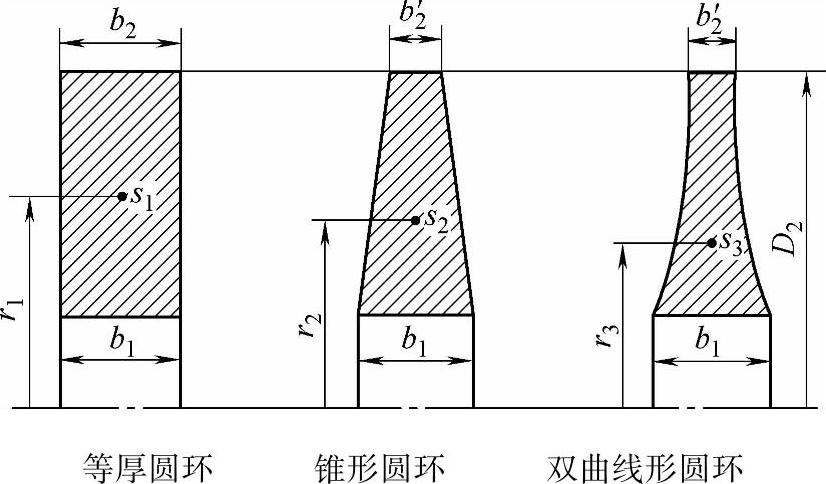
图7-27 三种不同轴向尺寸的圆环
不难看出,等厚圆环截面重心s1离轴线最远,比锥形和双曲线形圆环的圆周速度大,故等厚度圆环的应力最大,锥形和双曲线形圆环的应力依次减少。由此可知,应力与轴向尺寸有关。b2与b1的比值称为厚度比z,当厚度比z=b2/b1小,则应力σt小。
总的来说,圆环尺寸和形状对应力的影响,都与截面重心处的圆周速度的平方有关。因此在相同材料时,设计轮盘形状应尽量使截面重心处的圆周速度最小。也就是要使截面重心尽量降低。
2)轮盘应力计算基本公式。计算轮盘应力,先不考虑前盘、后盘、叶片等的相互影响,不论前盘、后盘形状如何,均按自由旋转等厚度圆盘处理。
①等厚度轮盘应力计算基本公式:

式中,σr为轮盘任意半径上的应力;μ为泊桑比。
等厚度轮盘以等角速度ω旋转时,由式(7-40)可以计算出任意半径上的应力。其应力分布如图7-28所示。从图中所示应力分布中,可得出一个重要结论:最大的切向应力发生在内径处。
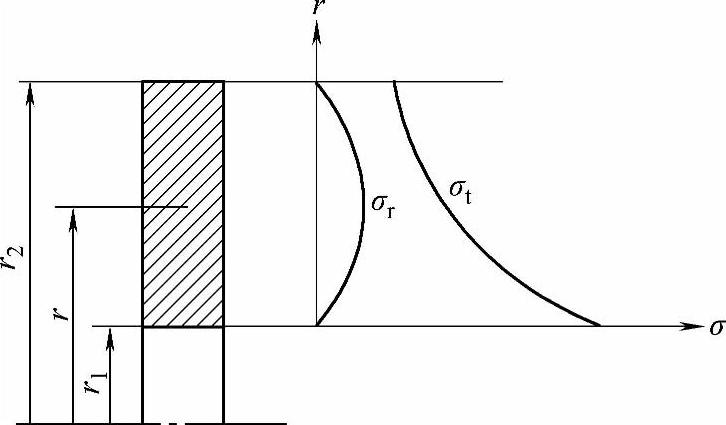
图7-28 等厚度轮盘的应力分布
②不考虑叶片的影响时,轮盘内径处的切向应力:
当r=r1时,由式(7-40)得
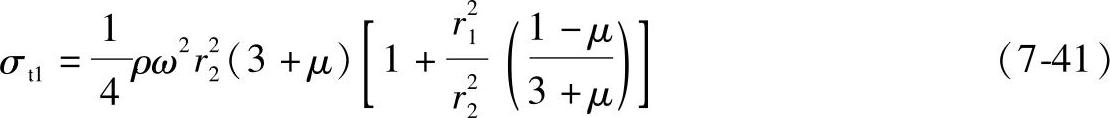
或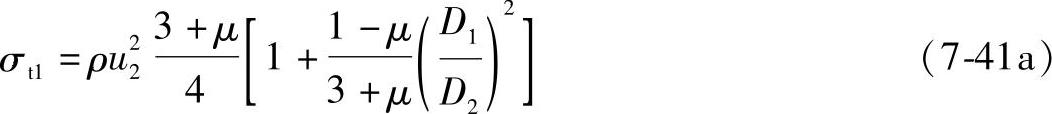
式中,ρ为轮盘材料的密度(kg/m3),钢材ρ=7.85×103kg/m3;u为轮盘外径处圆周速度(m/s);μ为材料的泊桑比,钢材μ=0.3; 为轮盘内、外径的比值。
为轮盘内、外径的比值。
将ρ、μ等数值代入(7-41a),得
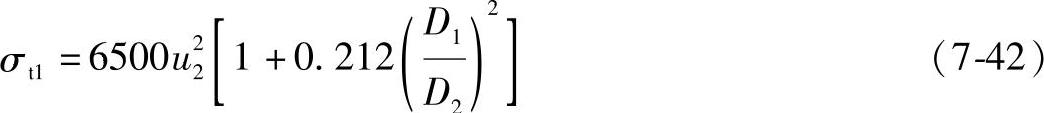
③考虑叶片的影响时,轮盘内径处的切向应力。前面考虑的是光轮盘由于离心力引起的应力计算。现在考虑叶片的离心力时,会使轮盘中的应力增加,即轮盘总应力为光轮盘与由于叶片而产生的附加应力之和,即
σt=σt1+σt2(7-43)
若光轮盘的离心力为F1,而叶片的离心力为F2′,则

其中,轮盘自身质量的离心力F1(N)为

或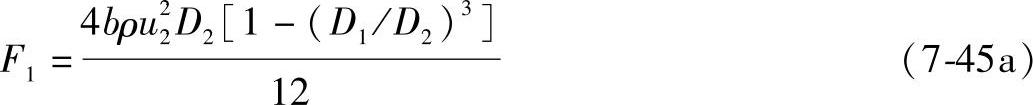
式中,ρ为轮盘材料的密度(kg/m3),钢材ρ=7.85×103kg/m3;b为轮盘厚度(m);ω为叶轮旋转的角速度(1/s);D1、D2为轮盘的内、外径(m)。
叶片的离心力F′2为 叶片数的单个叶片离心力在法线方向的投影之和,即
叶片数的单个叶片离心力在法线方向的投影之和,即

式中,z为叶片数,对双吸入风机,取单侧叶片数;K为分配系数,对前盘取K=0.5,对后盘取K=1;F2为一个叶片产生的离心力(N),F2=mRwω2m为一个叶片的质量(kg)R为每个叶片重心到叶轮中心距离(m)ω为叶轮旋转的角速度(1/s)。
通过式(7-45a)和式(7-46)计算F1F2′后,即可按式(7-44)计算σt2,再由式(7-43)求得轮盘内径D1处的总应力σt。
(3)叶片强度的计 离心通风机和轴流通风机的叶片,主要受本身离心力所产生的弯曲应力和拉应力。根据不同叶型,求出叶片的最大应σmax,然后进行强度校核:
σmax≤[σ]
式中,[σ]为许用应力(Pa)。
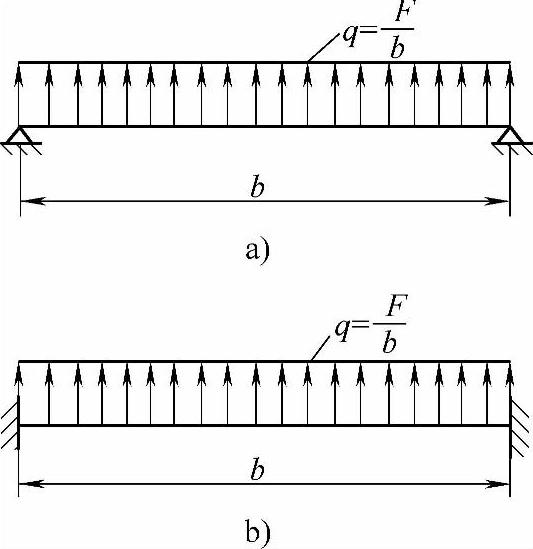
图7-29 叶片受力的简化图
叶片与前、后盘的连接,一般采用焊接或铆接结构。计算叶片强度时,假定叶片为一简支梁,如图7-29a所示;或是一固定梁,如图7-29b所示,叶片因旋转产生的离心力假定为在梁上均匀分布载荷。
根据假定条件,简支梁承受均布载荷时,最大弯矩产生在梁的中央,即 处,且最大弯矩为
处,且最大弯矩为
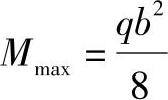
式中,q为均布载荷在梁的单位长度上的重量(N/m)。
固定梁受均布载荷时,最大弯矩发生在梁的两端,且最大弯矩为

叶片的最大弯曲应力为

式中,W为抗弯截面模数(m3)。
1)平板叶片的强度计算。图7-30所示的叶轮,配有安装角为β的直叶片。
假定叶片重心在O点,当叶轮以角速度ω旋转时,单个叶片所产生的离心力为F=ρω2blδR式中,ρ为叶片材料的密度(kg/m3),钢材ρ=7.85×103kg/m3;b为叶片平均宽度(m);ω为叶轮旋转的角速度(1/s);l为叶片长度(m);δ为叶片厚度(m);R为叶轮中心至叶片重心的半径(m)。
将离心力分解成沿叶片的法向力F1和切向力F2,在F1和F2的作用下,在相应方向发生弯曲。由于F2方向的叶片抗弯截面模数较大,相应F2引起的弯曲应力较小,可以忽略不计。而只计算由F1引起的弯曲应力。

图7-30 平板直叶片受力分析
由图7-30可知F1=Fcosβ
则叶片的荷重集度为
叶片的抗弯截面模数为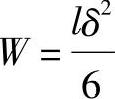
若按简支梁计算,则叶片最大弯矩为

叶片最大弯曲应力为

若按固定梁计算,则叶片最大弯矩为

叶片最大弯曲应力为

或
式中,n为叶轮的转速(r/min)。
2)圆弧叶片的强度计算。
①圆弧窄叶片。这种叶片的特点是叶片的径向尺寸大于叶轮的轴向尺寸。计算时,假设在叶片上沿轴向截取长度为l,宽度为b的一个小窄条,将这个小窄条看作是承受均布载荷的梁,叶片重心近似在叶片工作面的O点上,如图7-31所示。显然,这小窄条就相当于一个平板叶片,其计算与平板直叶片相同,可根据叶片与前、后盘的连接是铆接结构或焊接结构,按简支梁或固定梁采用式(7-48),或式(7-49),式(7-49a)计算。
由以上计算公式可知,最大弯曲应力与Rb2cosβ成正比;而Rb2cosβ值随截取小窄条位置不同而不同。因此在强度计算时,应视具体情况选定危险截面位置,例如叶片进口处,使计算出的弯曲应力为最大值,或取几个不同位置进行验算,而取其较大者。
②圆弧宽叶片。这种叶片如图7-32所示,其特点是叶片的径向尺寸小于叶轮的轴向尺寸。此时分力F2引起的弯曲应力不能忽略,在强度计算时,把整个叶片看成承受均布载荷的梁。
单个叶片产生的离心力为
F=ρr2αδbω2R
式中,r为叶片圆弧半径(m);2α为叶片圆弧所对中心角(rad)。

图7-31 圆弧窄叶片受力分析
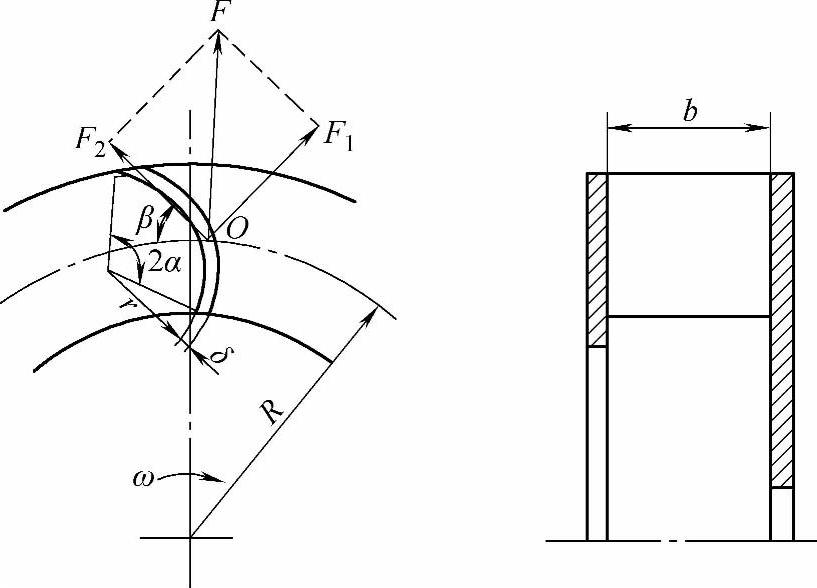
图7-32 圆弧宽叶片受力分析
假定叶片重心在其工作面o点上,将离心力F分解为法向F1和切向分力F2,则
F1=FcosβF2=Fsinβ
当将叶片看作承受均布载荷的简支梁时,因F1和F2的作用,使叶片产生的最大弯矩为

当将叶片看作承受均布载荷的固定梁时,因F1和F2的作用,使叶片产生的最大弯矩为

这时,可用下式求出叶片相应的抗弯截面模数:
W1=r2δk1W2=r2δk2式中,k1、kk2为系数,其值可根据角αα的大小,查表7-6。
表7-6 系数k1、k2值
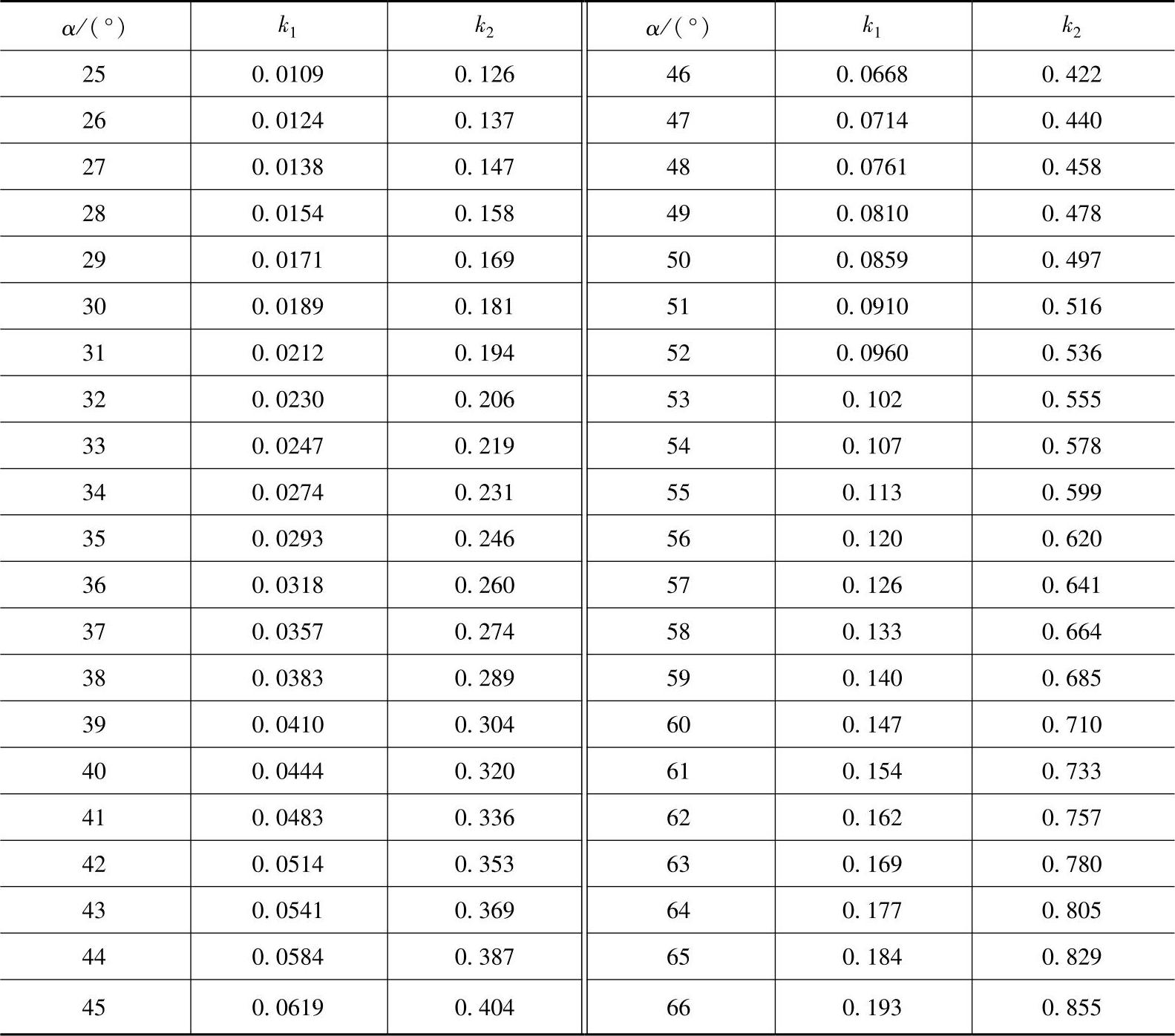
因F1和F2的作用,使叶片产生的最大弯曲应力分别为

总的叶片最大弯曲应力为
σmax=σ1max+σ2max
3)机翼形叶片的强度计算。一般机翼形叶片的工作面是弧形。除小型叶片以外,一般用钢板做成空心。为了增加叶片刚性,经常在叶片内部加设加强筋板。但在强度计算时,可不考虑筋板对强度的有利影响,把整个叶片看作承受均布载荷的梁。当叶片以角速度ω旋转时,单个叶片因本身重量产生的离心力为
F=mRω2
机翼形叶片见图7-33。将叶片形状近似按椭圆形考虑,叶片的重心就是椭圆形的形心o。通过O点将叶片离心力分解为沿叶片的法向力F1和切向力F2。显然,离心力F方向的抗弯截面模数较大。其强度计算方法与平板直叶片类似,仅计算F1所产生的弯曲应力。
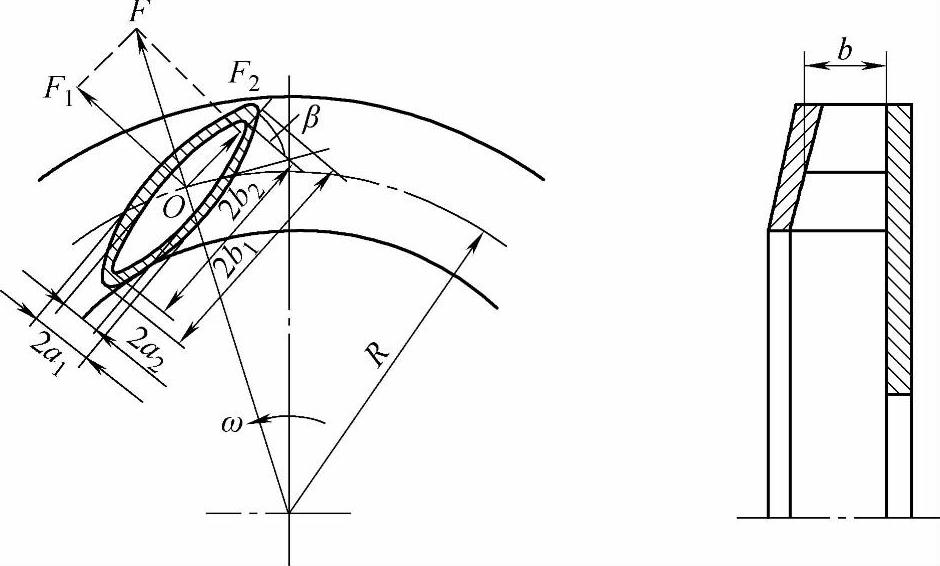
图7-33 机翼形叶片受力分析
由图7-33可知:
F1=Fcosβ=mRω2cosβ (7-50)
式中,m为单个叶片的质量(kg);R为叶片重心至叶轮中心的距离(m);β为半径R处叶片的安装角。
叶片的抗弯模数W1可由下式求出:
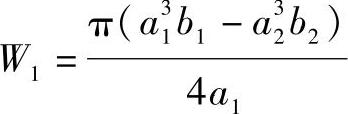
按固定梁计算时,叶片的最大弯矩为

按简支梁计算时,叶片的最大弯矩为

叶片最大弯曲应力为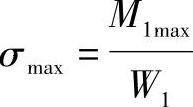
(4)铆钉的强度计算
1)叶片与前、后(中)盘连接铆钉的最大切应力。当叶轮旋转时,叶片与前、后(中)盘连接的铆钉承受叶片离心力。在计算时,假设叶片与前、后(中)盘连接铆钉承受叶片离心力的50%,而叶片与后盘的连接铆钉承受叶片离心力的100%。
铆钉的切应力为

式中,F为单个叶片的离心力(N);d为铆钉直径(m);z为铆钉数量;K为分配系数,对前盘K=0.5,对后盘K=1.0。
2)后盘与轮毂连接铆钉的切应力。当叶轮在转速为n、功率为P的情况下工作时,其扭矩为

式中,n为叶轮转数(r/min);N为风机所需功率(kW)。
则铆钉的切应力为

式中,R为后盘与轮毂连接铆钉所在的圆半径(m);z为铆钉数量;d为铆钉直径(m)。
(5)轮毂(轴盘)材料选用的计算 轴盘在选择材料时,可根据轴盘最大直径d处的圆周速度ui来确定。图7-34为轴盘示意图,其圆周速度ui的计算式为

式中,d为轮盘最大直径(m);n为叶轮转速(r/min)。
当ui小于30m/s时,可选用一般铸铁,如HT250;当ui大于30m/s小于40m/s时,可选用较高级的铸铁,如HT350;当ui大于40m/s时,应选用铸铁,如ZG230-450,也可选用经热处理后韧性较高的墨球铸铁,如QT450-10。
有关建筑及空调风机的工程设计、使用与维修的文章

特别需要指出的是:在相似条件下,两个通风机的比转数是相等的。当进口状态是非标准或气体种类不同时,比转数的计算要考虑气体密度的变化。标准状态气体的密度为1.2kg/m3则比转数为比转数可以用量纲一的参数、来表示:对于标准进口状态,ρ=1.2kg/m3,则比转数为在离心通风机中,有时采用双面进气形式,以扩大流量范围。轴流通风机采用双级形式,以提高升压,而一般的比转数公式是按单级单面进气计算的。......
2023-08-20

2)先选择模型通风机,由模型通风机的比转数ns及换算好的流量qV、全压p计算出所需要的转速。进行通风机的结构设计,并验算零部件的强度。因此相似设计在通风机设计中被广泛采用。解:1)p′=9.807×264Pa=2589Pa将流量、全压换算为进口状态:qV=qV′=49400m3/h=13.72m3/s2)如果选用4-13.2通风机,转速n取1450r/min,其比转数为由4-13.2型通风机的性能曲线求得:=0.437、=0.23、η=0.93,便可计算u2、D2及功率P。......
2023-08-20

沿程损失的计算 气体在横断面不变的管道内流动时,沿程损失hf可按式计算:沿程压力损失Δpm为式中,Δpm为管道的沿程压力损失;λ为沿程(摩擦)阻力系数;c为管道内气体的平均流速(m/s);ρ为气体的密度;l为管道的长度;d为管道的直径。沿程压力损失也可表示为而单位长度的沿程损失,通常称为比摩阻,用符号pm表示。对于长、宽分别为a和b的矩形管道为沿程阻力系数可按式计算:......
2023-08-20

根据上述防噪原理,下面介绍几种通风机噪声控制的主要方法。合理选择通风机的转速大小,这是因为通风机的噪声与转速是6次方比例关系。这种通风机与同性能的一般通风机比较,噪声下降15方左右。噪声衰减性能与吸声材料的密度、厚度、小孔的直径d,以及开口度有关。式说明,减噪量主要取决于壳体长度L和填充于内表面的吸声材料的吸声率。为了尽量降低电动机噪声,往往采用内表面贴有吸声材料的防声罩,阻止噪声的向外扩散。......
2023-08-20

测量风机转速的仪表及方法很多,目前常用的是光电转速传感器和转速数字显示仪。这两种仪表精度高、误差很小,但转速数字显示仪必须与转矩转速传感器配套使用,因此操作复杂。机械转速表测量误差大些。图9-5 转矩转速传感器光电转速传感器 使用光电转速传感器测量转速时,要在被测量旋转轴的表面上涂上黑白相间的条纹各z条。而后使光电转速传感器照射有条纹的轴表面。......
2023-08-20

能量方程式是建立流体通过旋转叶轮时,获得能量的定量关系式。此方程式是欧拉在1756年首先推导出来的,所以又称欧拉方程。能量方程的表达式 已知原动机传给风机轴的功率P为P=Mω式中,M为通风机叶轮轴的力矩(N·m);ω为通风机叶轮的旋转角速度(1/s)。pT∞=ρ 式即为能量方程的表达式。能量方程式的修正 实际情况下,叶轮叶片数有限,流体具有粘性,因而实际应用时,应对式进行修正。......
2023-08-20

按照形成的原因,可分为沿程阻力损失和局部阻力损失两种。摩擦产生的热量加热流体及所接触的物体,并通过固体边界散失到外界环境中去,这就是通常说的流动阻力产生的机械能损失。沿程阻力引起的能量损失,称为沿程阻力损失,简称沿程损失,用符号hf表示。流体在流过固体边界急剧变化的区域时,能量损失主要集中在该区域及其附近,比如管道转弯、管道直径变化、管道阀门半开节流等。......
2023-08-20

流体在空间的流动可以说都是三元流动,运动参数是空间三个坐标的函数。因此对于工程技术中的问题,在保证一定精度的条件下,尽可能将三元流动简化为二元流动,甚至一元流动来求近似解。流场的运动参数只是两个坐标的函数时称为二元流动。若实际流体的粘性很小,可以忽略,以管横截面上的平均流速来描述管内流动,即将二元流动化为一元流动求解。图2-3 圆管内流动a)二元流动 b)一元流动......
2023-08-20
相关推荐