批评按照公平市场价值标准补偿的观点认为，征收补偿的范围应当覆盖被征收财产所有人所遭受的全部损害，不仅包括财产的客观价值，还应当包括依附于财产的主观价值。法院也已经承认，“在一些案件中，按公平市场价值标准补偿不能充分地补偿财产所有者的损失”。据此，征收扣动了计算财产权社会义务承担的扳机，按公平市场价值标准支付给财产所有人的补偿当中，其原负担的财产权社会义务理应被扣除。......
2023-07-16
复合校正中按扰动补偿的优化方法
【摘要】：图6-20按扰动补偿的复合控制系统引入扰动补偿后，扰动作用下的误差为显然，选择前馈补偿装置的传递函数为这时有En=0，即扰动对系统的输出和误差无影响。但是，由于物理系统传递函数的分母阶数总是大于分子的阶数，按式、式实现误差全补偿的条件在物理上往往无法准确实现。图6-21例6-4复合控制系统结构图解：由式有输入，所以有要使esr=0，Gc的最简式应为可见，引入信号微分作为前馈补偿后，完全消除了斜坡信号作用下的稳态误差。
按扰动补偿的复合控制系统如图6-20所示，其中N（s）为可测量扰动，Gc（s）为前馈补偿装置。
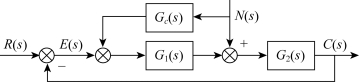
图6-20 按扰动补偿的复合控制系统
引入扰动补偿后，扰动作用下的误差为
显然，选择前馈补偿装置的传递函数为
这时有En（s）=0，即扰动对系统的输出和误差无影响。因此，称式（6-27）为对扰动的误差全补偿条件。
采用前馈补偿控制并没有改变系统的特征方程，但可以减轻反馈控制的负担，适当降低反馈控制系统的增益，有利于系统的稳定。前馈补偿通过预先产生一个补偿信号去抵消由原信号通道产生的误差，以实现消除系统误差的目的。
但是，由于物理系统传递函数的分母阶数总是大于分子的阶数，按式（6-25）、式（6-27）实现误差全补偿的条件在物理上往往无法准确实现。因此在实际应用中，为了使补偿装置的结构简单，容易实现，并不要求实现全补偿，只需采用主要频段内近似全补偿或稳态全补偿。
例6-4 复合控制系统结构图如图6-21所示，其中K1，K2，T1，T2是大于零的常数。当输入r（t）=V0t·1（t），选择补偿装置Gc（s），使系统的稳态误差为0。
图6-21 例6-4复合控制系统结构图
解：由式（6-24）有
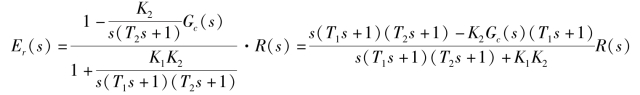
输入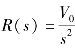
，所以有
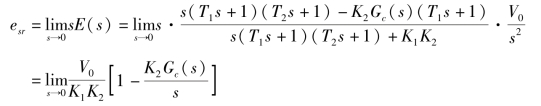
要使esr=0，Gc（s）的最简式应为
可见，引入信号微分作为前馈补偿后，完全消除了斜坡信号作用下的稳态误差。这就是稳态全补偿，它在物理上更易于实现。
有关自动控制原理的文章
- 详细阅读
-
土工复合软体排的制造方法优化技巧详细阅读
现在我国多使用丙纶长丝和涤纶长丝，土工复合软体排在工程应用中均符合设计要求。图10-4-8 软体排生产工艺流程⑥软体排的缝纫必须由设计单位提供断面图和有关水文资料。为配合软体排的应用，最好由生产工厂、施工单位到工地现场讨论进场前的有关准备工作。缝制图绘制后应由设计、施工和工程单位共同认可，以便相互监督，并作为验收交货的依据。......
2023-06-20
-
复合材料的特性及其优化方法详细阅读
飞行器结构中使用的复合材料，主要是纤维增强树脂基复合材料。图10-4给出了先进复合材料比强度及比模量的范围。表10-1各种材料的力学性能续表由图10-4及表10-1可见，FRP 的密度约为钢的1/5，为铝的1/2。表10-2各类复合材料的主要性能2.纤维增强树脂基复合材料的缺点除上述一系列优点外，纤维增强树脂基复合材料也存在一些问题，比如设计制造复杂、层间承载能力低及原材料成本较高等。铝锂合金的价格是碳纤维复合材料的1/10。......
2023-07-18
-
使用SIWATOOLCS软件进行秤校优化方法详细阅读
在电脑上安装SIWATOOL CS软件后，可通过RS232串口连接到SIWAREX CS模块进行校秤。使用SIWATOOL CS校秤，只需在模块正确通电后即可，而与CPU是否运行，是否进行了组态编程等无必要关系。图11-45 SIWATOOL CS与PC的通信单击“Online”通过RS232建立电脑与称重模块的连接，如果建立连接时，在不断的重试，请检查接线及通信设置。图11-47 显示重量变为0.00kg图11-48 修改校正砝码图11-49 校准砝码重量为200kg选择发送，将校正砝码重量写入SIWAREX CS模块中。图11-52 状态信息及故障信息......
2023-06-18
-
复合材料制件表面质量检查的优化方法详细阅读
复合材料制件表面质量通过目视来检查，表面质量的通用验收要求如下。若没有纤维损伤，表面树脂划伤是可以接受的。②靠工装面与靠袋面的表面凹坑。④可见的材料夹杂，夹杂材料长度一般要求不大于12.7 mm。没有纤维暴露的任何表面含胶是允许的。⑦零件表面不允许有纤维铺层皱褶。⑨零件表面不平整，除了图样上允许的拼接或铺层终端引起的台阶，表面不平整应在0.254 mm 以内。⑩圆角处架桥，小于或等于0.5 in 长的圆角处架桥是允许的。......
2023-07-18
-
制备方法及性能评价：梯度功能复合涂层的优化详细阅读
等离子喷涂制备梯度功能复合涂层的方法见表4-27。表4-27 等离子喷涂制备梯度功能复合涂层的方法在采用单枪法喷涂梯度功能复合涂层时，要注意控制两种成分的飞行轨迹尽可能保持一致，以形成相同的束斑。否则，两种材料不会沉积在相同位置，其中的一种材料成分会出现富集区，甚至形成不均匀带状结构，这将严重影响梯度功能复合涂层性能的均匀性。需要说明的是，上述梯度功能复合涂层均不是严格意义上的梯度结构，而只是多层阶梯结构。......
2023-06-18
-
激光-电弧复合焊技术优化详细阅读
下面分别以激光-TIG和激光-MIG电弧复合热源焊为例描述激光与电弧的相互作用。由于TIG焊不存在熔滴过渡对焊接熔池的影响，在激光-TIG电弧复合热源焊过程中，熔池匙孔的稳定性较好。尤其是对于CO2激光，焊接过程中的光致等离子体较多，对电弧的影响也更明显。此外，复合焊接机制的转变还与激光束和电弧的复合方......
2023-06-26
-
无人炮塔的复合控制策略优化详细阅读
将式代入式，可得式中，fZ2为观测器的估计误差。定理6.2对无人炮塔系统，当σ＞κe成立时，在采用形如式的快速非奇异终端滑模面和形如式的控制律时，可保证滑模面S和跟踪误差eq能在有限时间内收敛到零点。......
2023-06-24
相关推荐