广义地说，数字微波通信系统设备由用户终端、交换终端复用设备、微波站等组成，如图7-2所示。狭义地说，数字微波通信系统设备指微波站设备。微波站的基本功能是传输来自终端站、分路站、枢纽站和中继站的信号。配有交叉连接设备，除了可以在本站上、下收发波道的部分支路信号外，可以沟通干线上数个方向之间通信的微波站称为枢纽站。......
2025-09-29
热力学流体力学基础解析
【摘要】：总压p0是在等熵过程静止状态下的流体压力。但是，总压是以可逆绝热过程停止时获得的压力。图12-6 滞止状态动量守恒定律 加速或减速运动的所有流体与正常状态或非正常状态无关，任何状态下都满足牛顿第二定律。如果把式的作用力和速度以不是矢量的标量成分进行表示，x方向和y方向的动量守恒定律为角动量守恒定律 涡轮机构是流体改变旋转叶片的动量，相反旋转的叶片对流体做功，以提高流体压力的机械装置。
喷气发动机假设工质流体空气（或燃烧气体）为理想气体，且气体流动为正常状态，且把推进发动机的所有过程假设为理想气体正常流动来进行说明。
1.能量守恒方程
压缩器、燃烧器、涡轮的气体流动相关正常状态能量守恒方程为
式中，q、w分别为通过系统分界的热量和功，下标1、2分别表示系统的进口和出口。如果使用焓定义式h=u+pv，并忽略进口和出口的势能变化，上式可变化为
式中，V为工质流体速度。通常，压缩器、涡轮、喷管、扩散管内的气体流动假设为绝热过程（q=0）。
压缩功或涡轮功根据能量守恒方程（12.7）推导出
喷管或扩散管仅为工质流体的通道，如果忽略摩擦热，可以视为等焓过程，正常状态能量守恒方程根据式（12.7）可以推导出
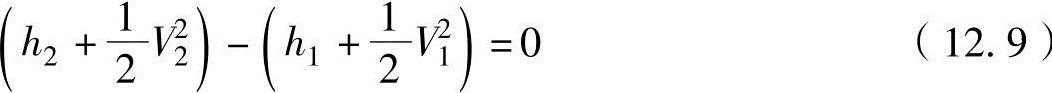
或
2.总参数
总参数是说明可压缩性流动时表示气体状态的量，是流体以等熵过程（可逆绝热过程）减速到速度为0时的状态参数。总参数以下标0表示，分别以T0、p0、ρ0、h0表示总温、总压、总密度和总焓。使用总参数可以在说明压缩性流动时更为简便一些。
由正常状态能量式（12.9）可知，焓与动能项始终一起出现，可以把这两项组合为一项表示，即
式中，h0为总焓（Stagnation Temperature）；h为静焓（Static Temperature）。如果假设流体为质量热容为常数的理想气体，焓h可以用cpT代替，可以把式（12.10）表示为如下的温度相关式：
式中，T0为总温（Stagnation temperature），表示速度为0状态下的温度；V2/2cp为流体速度从V降低到0的过程中流体温度上升值，称为动态温度。在低速流动状态下，值较小，静温度T与总温T0相同。但是在高速流动状态下，利用固定传感器测量的温度（总温T0）比静温度T高很多，其差值就是动态温度。
总压p0是在等熵过程静止状态下的流体压力。根据等熵过程的状态方程式Tp（1-k）/k=常数的理论，理想气体的总压p0与静压（静压力）p之间的关系为
如果把压缩功或涡轮功w用总参数进行表示，根据能量守恒方程（12.8）可以更为简单地表示为
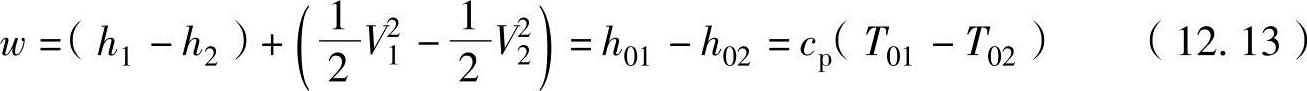
如果燃烧器中的加热量q用总参数表示，则从能量方程（12.7）可以推导出
q=h02-h01=cp（T02-T01） （12.14）
从式（12.13）和式（12.14）中可以得出，当没有热量和功的传递，总焓与总温保持一定值。
h01=h02或T01=T02
如果流体在端面积不均匀的管内流动会产生摩擦产生热量，使静温度发生变化，但总温不会发生变化。
总焓与总温是当流动停止时获得的焓和温度。但是，总压是以可逆绝热过程停止时获得的压力。因此，总压不同于总温，仅在没有热量和功传递的喷管和扩散管中的可逆绝热流动过程（等熵过程）中保持一定。总压的降低利用在流体摩擦尺度上。总压p0、总温T0可以在等熵过程的p-T线图上显示其状态参数，作为决定任意流体状态的热力学状态参数（性质）。
如图12-6所示，在T-s线图上同时显示了静态1与2之间压缩过程的总参数和静态参数。在图中点线表示理想过程（等熵过程），实线表示增熵的实际过程，数字上的上标撇（′）表示理想过程。因此，在状态1与2之间的压缩过程中，出口总压在理想过程中以02′表示，实际过程中因非可逆性成为点02。
3.动量、角动量守恒定律
喷气式原理是利用进气的空气动量变化获得推进力，动量守恒定律是解释涡轮喷气发动机的核心。(https://www.chuimin.cn)
图12-6 滞止状态
（1）动量守恒定律 加速或减速运动的所有流体与正常状态或非正常状态无关，任何状态下都满足牛顿第二定律。即，所有物体如果不受外力的作用或作用力的合力为0，物体保持恒定速度和以0加速度移动，如果合力不是0，则物体的加速度与作用力的大小成正比。
动量（线性动量）M是指质量m的物体以速度V运动，其定义为
M=mV （12.15）
把牛顿第二定律以动量的观点解释为
式中，左侧Fdt称为冲量；右侧d（mV）称为动量变化量。作用力F（或ΣF）和速度V以矢量表示，应注意其方向。此方程式表示动量随时间的变化率d（mV）/dt等于作用在物体上的作用力（外力）F，并且在任何方向施加的冲量Fdt等于动量变化量d（mV）。如果没有外力作用（F=0），则式（12.16）可以用下式表示。
d（mV）=mV2-mV1=M2-M1=0 （12.17）
M2=M1或mV2=mV1
这被称为动量守恒。
如果把式（12.16）的作用力和速度以不是矢量的标量成分进行表示，x方向和y方向的动量守恒定律为
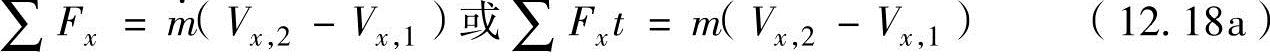
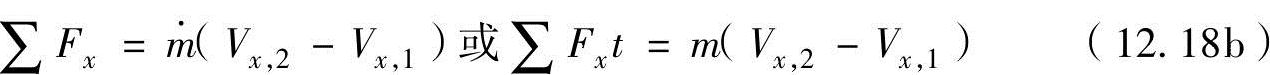
（2）角动量守恒定律 涡轮机构（涡轮、压缩器）是流体改变旋转叶片的动量，相反旋转的叶片对流体做功，以提高流体压力的机械装置。这样的机械流体力学问题方面，转矩与角动量很重要。
角动量H定义为空间上以旋转中心O开始在位置r的地点位置半径r与线性动量M（=mV）之积。
H=r×M=r×mV （12.19）
对角动量进行微分可得
转矩（旋转力）τ定义为位置向量r与力矢量F（=mV）之积，根据上式对角动量的微分等于转矩。
式（12.20）表示外部作用转矩r等于角动量的变化量dH/dt。如果没有外部作用转矩（τ=0），从式（12.19）和式（12.20）可得
H2=H1或r2×mV2=r1×mV1 （12.21）
式（12.21）被称为角动量守恒。
如果把式（12.20）利用标量成分表示，可以表示为
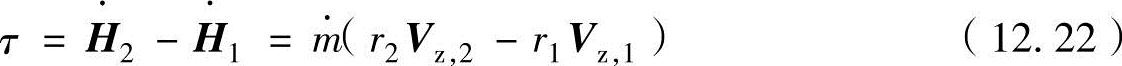
涡轮机构以ω角速度旋转时，式（12.22）可以表示为
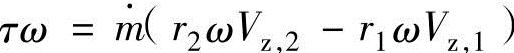
式中，τω相当于涡轮机构的动力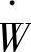
。在理想的离心泵中，流体的切线速度Vz与叶片的转速相同，因此Vz，1=ω1r1，Vz，2=ω2r2。把此公式代入到上式中，可得离心泵的转矩τ与动力
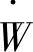为
动力
在作用于流体上的转矩与旋转方向相同的压缩器中为负（-）值，转矩与旋转方向相反的涡轮中为正（+）值。这表示压缩器的驱动要从外部获得功，涡轮的驱动会对外部做功。因此，在压缩器中角动量增加，在涡轮中角动量减小。
相关文章
- 详细阅读
-
湿地生态修复的理论基础解析详细阅读
当湿地生态系统结构发生变化，其生态功能减弱甚至丧失时，将导致湿地生态系统的退化。湿地生态系统结构和功能退化的原因是多方面的，其中最主要的是干扰。HGM原理与方法在城市湿地生态恢复过程中，对恢复效果的检测也是一项重要内容。HGM方法是一种快速评价人类活动对湿地生态系统功能影响的方法，它可以由湿地分类、湿地功能描述和参考湿地应用三个相关组成部分来描述。参照湿地，可以确定湿地生态系统的结构和功能状态。......
2025-09-29
- 详细阅读
-
深入解析2.5p-q功率基础理论详细阅读
而三相瞬时有功功率具有清晰且被普遍接受的物理意义，同时在暂态过程中也是适用的。图2-12给出了用两个瓦特表测量三相三线制三相负载平均功率的测量接线图。p-q理论是在三相系统中定义的，这里所指的三相系统可以有中性线也可以无中性线。......
2025-09-29
-
高速计数器的基础知识解析详细阅读
S7-1200 PLC提供了最多6个高速计数器，其独立于CPU的扫描周期进行计算，可测量的单相脉冲频率最高为100kHz，双相或A/B相频率最高为30kHz。每种高速计数器有外部复位和内部复位两种工作状态。表9-13列出了高速计数器的工作模式和硬件输入定义。表9-14为高速计数器默认地址列表。图9-20 高速计数器指令块表9-15 所示为高速计数器指令块参数......
2025-09-29
-
坐标变换的数学基础及应用解析详细阅读
上面方程式中的Mu和Mi与所需变换的坐标系相关，因此，该变换矩阵并不是唯一的。如果将式和式代入式可得IU==I′MiMuU′ 从上式可看出，当满足功率不变约束时，必须有下式成立：MiMu=1或者Mi=Mu-1 2.电压和电流具有同一变换系数矩阵的变换采用功率不变约束的变换，虽然能使变换成为唯一，但是其电压变换系数矩阵和电流变换系数矩阵可能并不相同。......
2025-09-29
-
弧焊电源的基础知识及工艺要求解析详细阅读
供给焊接电弧能源，并具有适宜于电弧焊电气特性的设备，称为弧焊电源。（一）弧焊电源的工艺要求1）引弧容易。埋弧焊为改变空载电压方式，电流电压应同时调节。（七）弧焊电源的负载持续率和额定电流弧焊电源的一个特点是断续工作，负载持续率表示弧焊电源工作状态的参数。......
2025-09-29
-
Modelsim基础教程详细阅读
图5.23 编译图5.24 编译完成3.启动仿真工具当设计文件“traffic_lights_state_machine.v”和测试文件“testbench.v”编译通过之后，启动仿真工具。图5.27中，弹出时默认选中第一个“No design object visibility”，需要改选为第二个“Apply full visibility to all modules”选项，第二个选项可以使模块内部及模块连接间的信号都能被观察到，能够帮助我们更好地进行调试，而其他选项只能看到部分信号。......
2025-09-29
相关推荐