润滑理论基础：雷诺兹方程式及油膜厚度与油压关系

2025-09-29 理论教育版权反馈

【摘要】：润滑理论是正确说明润滑膜内的压力变化的理论。发动机的液动部位存在油膜，其特性的理论解释是根据雷诺兹方程式进行的。在上述公式中代入x=0时的p=0和x=l时的p=0的边界条件，可以得出流量Q与积分常数C为把式代入式中，可以得到上述方程式表示了随润滑距离x的油膜厚度h与油压p之间的关系，是润滑理论中为最基本的重要公式。为了获得压力分布，利用式可以得到式中，Q为容积流量。

润滑理论是正确说明润滑膜内的压力（单位面积的负重）变化的理论。发动机的液动部位（润滑部位）存在油膜，其特性（负荷容量、压力分布、油膜厚度）的理论解释是根据雷诺兹方程式进行的。雷诺兹方程式是通过对黏性液体的那微-史托克运动方程式进行推导。

润滑相关雷诺兹方程式为

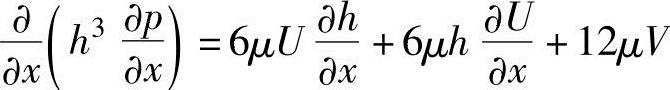
式中，p为油膜内的压力；h为任意位置；x为油膜厚度；μ为润滑油的黏性系数；U为两个摩擦面之间的滑动方向（x方向）的相对运动速度；V为y方向的相对运动速度。

上述公式的右边表示油膜内发生压力的三种基本形态，如图9-5所示。

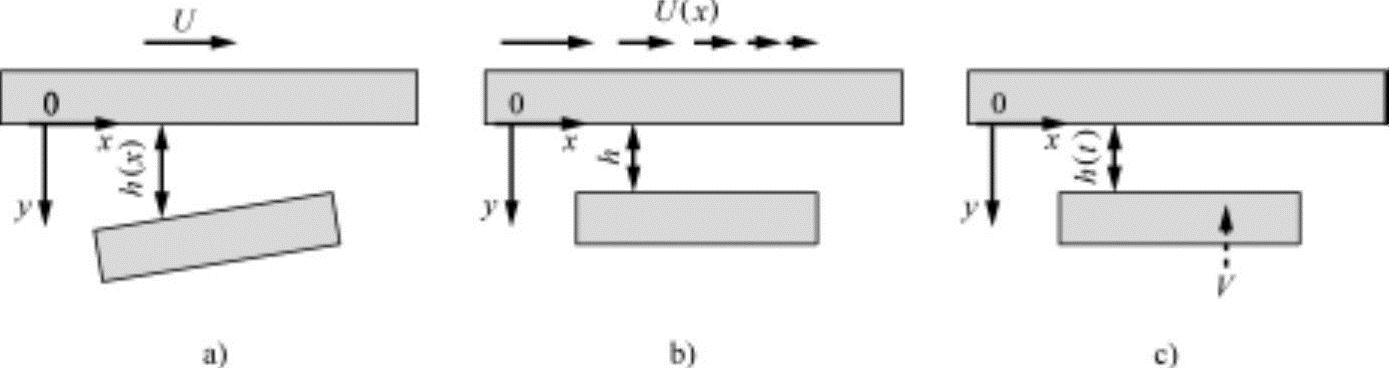
图9-5 油膜内发生的压力三种形态

①第一项为两个摩擦面之间有倾斜度，因此有厚度的变化。一侧固体面以相对运动速度U进行滑动的状态，即楔塞作用状态。

②第二项为两个摩擦面之间相互平衡，且滑动速度U发生变化的情况。

③第三项为平行的两个摩擦面之间以速度V在垂直方向彼此接近的状态，称为挤压作用。其中，第二项为h₁=h₂的平行面，不发生油压，负荷容量为0。发动机润滑的油膜负荷容量通常为第①项的楔塞作用和第③项的挤压作用。

1.滑动轴承

如图9-6所示，对长度为l的润滑停止面，运动面与停止面间隔油膜厚度h以速度U向x方向移动的滑动运动的情况进行分析。以油膜厚度为y坐标，与地面垂直的z方向的长度为无限长，并对润滑膜内微量容积适用那微-史托克方程式。如下进行假设：

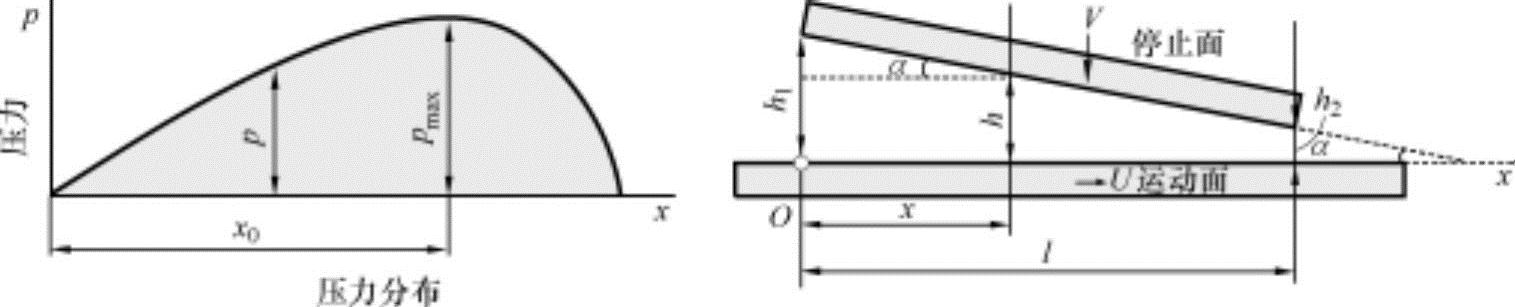
图9-6 平衡滑动轴承和压力分布

①流动是正常状态的层流。

②流体的惯性力远小于剪切力，因此可以省略。

③流体是非压缩性牛顿流体。

④油膜在厚度方向没有压力差。

⑤固体面与润滑膜的界面不发生相对滑动。

一维正常流动那微-史托克运动方程式为

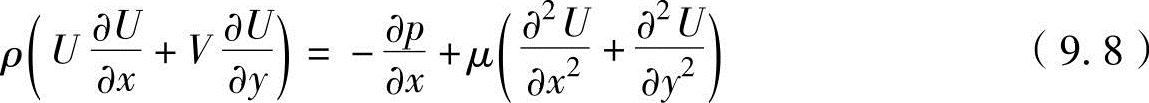
式中，U、V分别为移动物体方向的速度和垂直方向的速度；μ为黏性系数。如果适用前面的假设，因为是正常流动dV/dt=0，∂²U/∂x²=0，因固定面的斜率较小速度分布相同，并在油膜的厚度方向没有压力差，∂p/∂y=0。因此，压力p仅为x的函数，即可以看成p=p（x）。

如果考虑此条件，方程式（9.8）可以表示为

把上述方程对y进行2次积分，可以获得

式中，A、B为积分常数。在边界条件y=h时为U=0，在y=0时为U=U，把这些代入到上述方程式中，可以得到

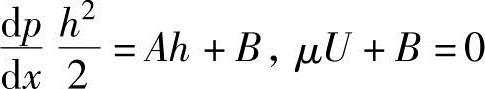
从上述方程式中求出A、B，并代入式（9.10）中，可以得到

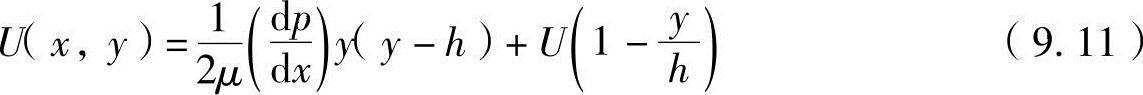
上述方程式为在润滑膜内任意位置（x、y）的流体速度。

在下边推导出润滑膜内任意位置的压力计算公式。润滑油量Q为在任意位置x通过油膜厚度h流动的量，如图9-6所示考虑地面垂直方向的单位宽度，可以用下述方程式进行计算。

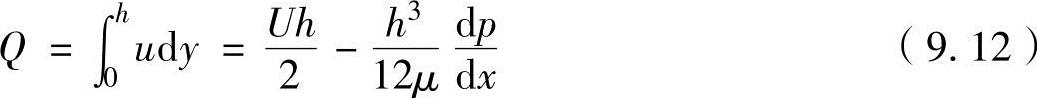
如果停止面的倾斜度为α，在图9-6的几何学形状上α=（h₁-h₂）/l，并在任意位置x的油膜厚度为h（x）=h₁-αx，代入这些公式并求出dp/dx为

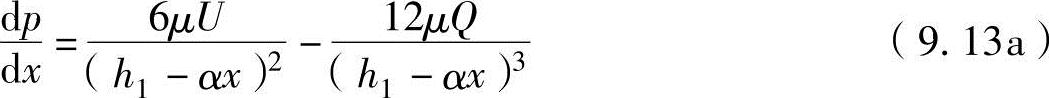
对于润滑油量Q，先设定与x无关，在上述方程式中进行对x的积分，可以推导出

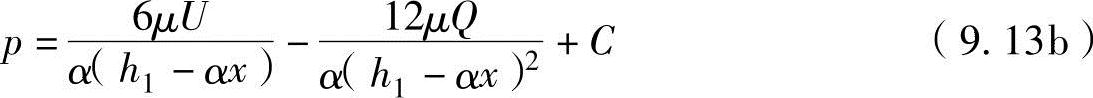
式中，C为积分常数。在上述公式中代入x=0时的p=0和x=l时的p=0的边界条件，可以得出流量Q与积分常数C为

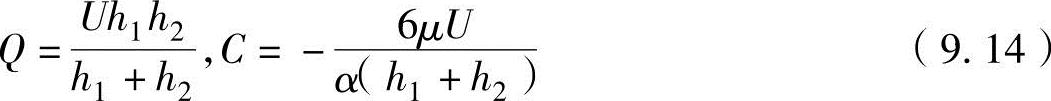
把式（9.14）代入式（9.13）中，可以得到(https://www.chuimin.cn)

上述方程式表示了随润滑距离x的油膜厚度h与油压p之间的关系，是润滑理论中为最基本的重要公式。这是因为随油膜厚度的变化而发生的压力要对应负荷容量的原因。滑动轴承的压力分布如图9-6所示。

对平板上作用的油压p用润滑长度l进行积分，可以得出在平板上作用的压力，假设在图中垂直方向单位宽度上作用的总压力（负重）为W，可以得出

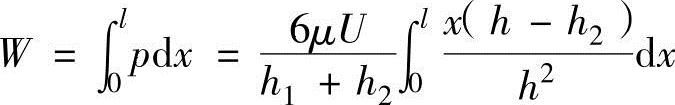
在上述方程式的右边代入h=h₁-αx并进行整理，可以得到

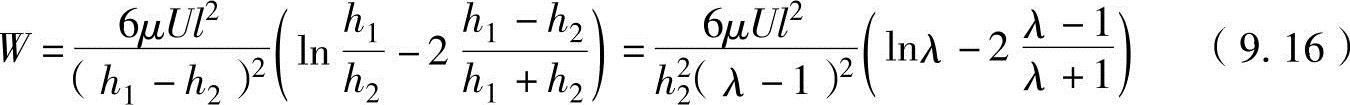
式中，λ为油膜厚度比（λ=h₁/h₂）。滑动轴承停止面的倾斜度α非常小，因而可以看成平板；总压力W等于轴承支撑的负重。

现在对润滑膜内的摩擦力进行分析。摩擦力F为对剪切力τ用润滑长度l进行积分的值，以下述方程式求出：

在上述方程式中，右侧的速度微分根据方程式（9.11）和式（9.13）可以推导出

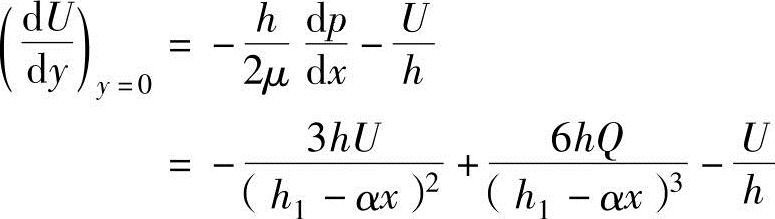
把此方程式代入前面的方程式中，润滑油内的摩擦力F计算公式为

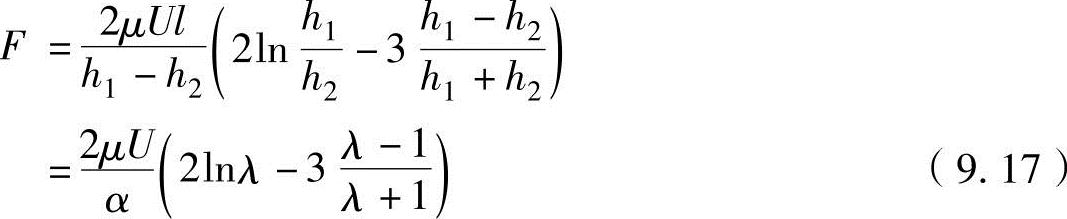
另外，对于最大负重W_max，可以在负重公式（9.16）中以用油膜厚度比λ进行微分的值为0，即dW/dλ=0的条件下求得，以此获得λ=2.2（h₁=2.2h₂）的值。因此对于最大负重和最大摩擦力，在式（9.16）和式（9.17）中代入λ=2.2，可以得到

因此，油膜内的平均摩擦系数f的计算公式为

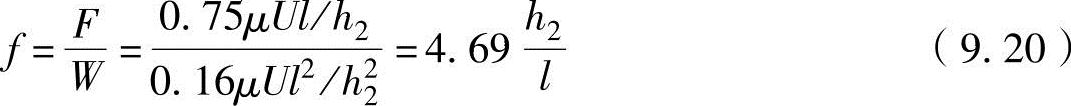
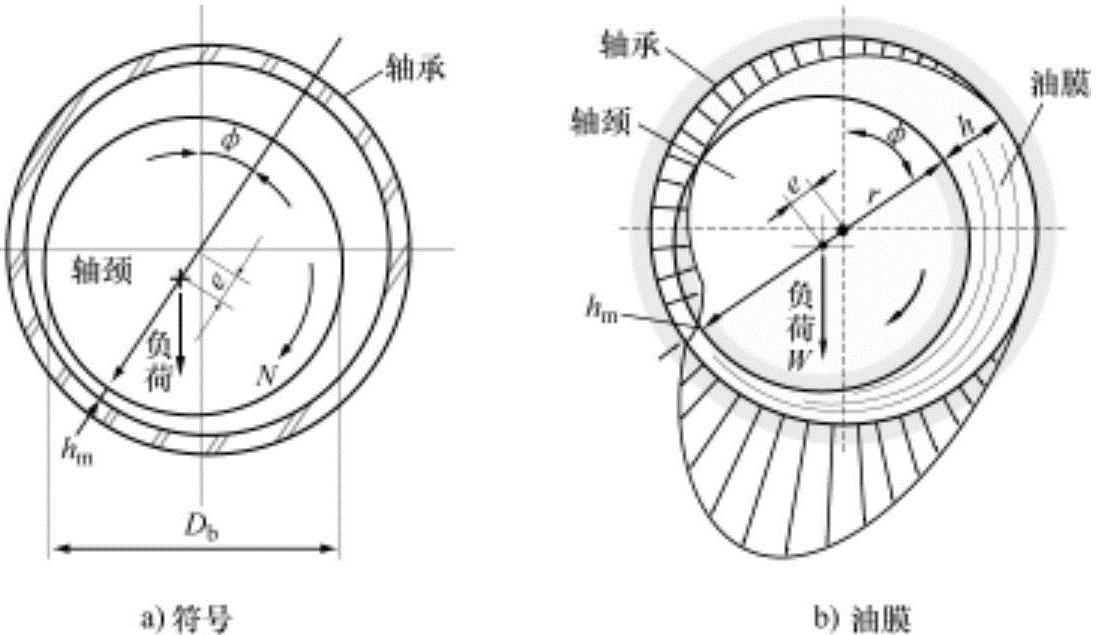
图9-7 轴颈轴承

2.轴颈轴承

对于轴颈轴承，可以对雷诺兹方程式进行稍微改动适用。轴颈轴承的概略图和油膜的压力分布如图9-7所示。轴颈轴承起润滑作用时，轴颈（轴）和轴承的中心如图9-7a所示处于偏心状态，轴颈（轴）旋转时形成楔塞型润滑油膜。

如果仅对楔塞作用进行分析，雷诺兹方程式（9.8）为

对上述方程式进行一次积分，可以得到

式中，C为负重常数，是根据油膜的形成状态决定的参数。

油膜厚度h为h=h（φ），用下述公式进行计算。

h=ecoSφ+δ （9.23）

式中，e为偏心量；φ为如图所示的圆周方向的各位置；δ为轴颈轴承与轴之间的通道宽度，δ=R-r，其中R为轴承半径，r为轴颈轴的半径。

如果假设h<<r，则可以把rdφ看成直线。为了获得压力分布，利用式（9.22）可以得到

式中，Q为容积流量。对于轴颈与轴承完全分离不接触的完全润滑轴承，油膜内压力p（φ）为φ的周期函数，即p（0）=p（φ）。对上述方程式（9.24）进行积分，可以获得下述方程式。

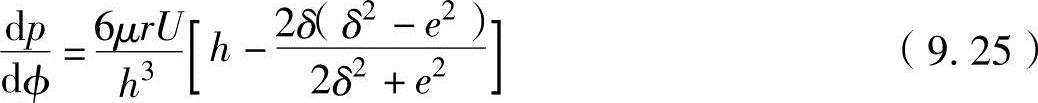
上述方程式表示了随轴颈轴承圆周方向位置φ的压力分布。如果已知偏心量ε，取dp/dφ=0，可以得出p_max和p_min。油膜内的压力分布为如图9-7b所示，它支撑施加在轴上的负重W。轴颈轴承能支撑的负重W等于在轴颈轴圆周上作用的压力与剪应力垂直成分之和，可以表示为

如果在上述公式中负重W保持不变，可以看出随着速度U的增加，偏心量ε会减小。在极限状态下，即U→∞时，有e→0。

通过上述公式可以推导出

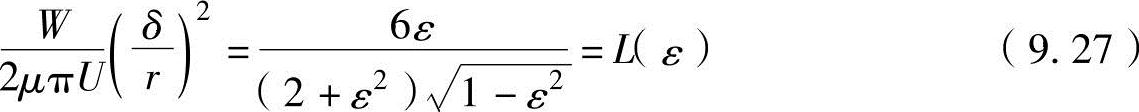
式中，ε（=e/δ）为相对运动偏心量。因此，如果对于得出的δ/r，W/U保持不变，即使W、μ、U发生变化，ε为常数。此关系式称为索末菲尔德相似准则，L（ε）称为在试验中制造模型尺度时有效使用的索末菲尔德数。最小油膜厚度随此值的减小而减小。即，作为轴颈轴承的基本定律，摩擦力、摩擦系数、油膜厚度、负荷容量等参数均以索末菲尔德数进行计算。

润滑理论基础：雷诺兹方程式及油膜厚度与油压关系

相关推荐