最大转矩电流比控制比较符合启动系统低速大扭矩启动过程的需要。图8.26永磁同步电动机双闭环矢量控制框图的差值。图8.26永磁同步电动机双闭环矢量控制框图当永磁同步电动机运行在恒转矩区时，直轴电流为已知值，交轴电流值根据直轴电流和PI调节器的限幅值决定。最大转矩/电流的控制方法就是当电动机输出力矩为某一值时，使定子电流的模值最小[6]。......
2023-06-23
启动过程中电动机转矩的控制优化
【摘要】：系统的启动过程，是指启动发电一体机在电池通电后转速上升，并带动发动机由静止状态达到最低点火转速，使发动机成功启动。发动机点火后，启动成功，电动机退出工作。为使系统的启动过程时间短、性能可靠，需针对不同阶段制定不同的启动转矩控制策略。为此，该阶段采用定占空比控制，使电动机电流尽可能平稳增长，进而产生波动幅度小的转矩，保证启动过程的平稳性。
系统的启动过程，是指启动发电一体机在电池通电后转速上升，并带动发动机由静止状态达到最低点火转速，使发动机成功启动。根据启动过程电动机的工作状态，可将其分成三个阶段：①初始阶段。此阶段电池直流电经逆变器逆变后变为交流电，供给电动机。受定子绕组阻抗的影响，电流不断增大，电动机并未开始运转。②加速阶段。该阶段电流增加，电动机转矩不断增大，其输出转矩大于负载转矩，电动机加速，带动发动机达到目标转速。③终止阶段。发动机点火后，启动成功，电动机退出工作。
为使系统的启动过程时间短、性能可靠，需针对不同阶段制定不同的启动转矩控制策略。
1.初始阶段电动机转矩控制策略
在启动的初始阶段，电动机输出转矩小于发动机阻力矩，电动机静止，电流迅速上升。为了缩短系统的启动时间，电动机从通电到转动的时间应尽量减小，所以需要加快电流的变化速度。根据前面的推导，电动机电流与电压满足如下关系：
设定不同的PWM占空比、电感系数、电阻Rs，可以得到不同参数影响下的电流曲线，如图8.33～图8.35所示。在启动静止阶段，PWM占空比、电感系数、电阻Rs对电动机电流均有不同程度的影响。PWM占空比通过电动机换相电路实现，占空比越大，电动机相电压的幅值越大，因此定子电流增加越快。定子电阻越大，同等电压值情况下的定子电流越小，故电流增加得越慢。电感系数越大，电流增加得越慢。因为电动机的电感系数和电阻值均为固定的参数，在电动机运转阶段不可调整，而占空比却可以通过控制电路来改变，因此，初始阶段占空比应取最大值1，以保证启动时间尽可能短。
为此，该阶段采用定占空比控制，使电动机电流尽可能平稳增长，进而产生波动幅度小的转矩，保证启动过程的平稳性。
2.加速阶段的电动机转矩控制策略
在加速阶段，采用转速电流双闭环控制逻辑，调节PI参数，使电动机转矩实时追踪发动机提供的负载转矩。转速环、电流环共有三个PI控制器，下文重点描述如何在线计算出各PI控制器的参数。
1）转速环PI调节器的参数整定
对于转速环PI调节器的参数整定，本书采用一种在线计算PI参数的方法。
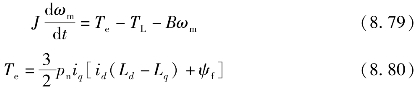
式中，ωm为电动机的机械角速度；J为转动惯量；B为阻尼系数；TL为负载转矩。
采用Harnefors F，Pietiliainen K等人在Torque-maximizing field-weakening control[8]中方法计算转速环PI调节器的参数，给出有功阻尼为
当采用零d轴控制策略时，并假定电动机在空载情况下启动，由上式可得到
将上式的极点配置到期望的闭环带宽β，能够推导出转速与q轴电流之间的传递函数为
联立上述两式，即可得到有功阻尼的系数Ba
采用传统的PI调节器，则转速环控制器的表达式为
因此，PI调节器的参数Kpω、Kiω可由下式整定：
式中，β为转速环期望的频带带宽。与采用典型Ⅱ系统进行PI调节器参数整定的方法对比，该方法参数调整与系统动态品质关系明确。
2）电流环PI调节器的参数整定
图8.41所示为典型的内模控制框图，其中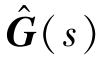
为内模，G（s）为被控对象，C（s）为内模控制器。
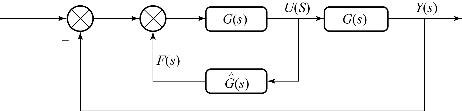
图8.41 内模控制框图
等效控制器为
I为单位矩阵。
如果内模建模足够准确，即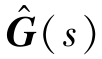
=G（s），则系统不存在反馈环节，此时系统传递函数为
因此，要保证系统稳定，只有当且仅当G（s）和C（s）稳定。
由于电动机的电磁时间常数远小于机械时间常数，电流环可近似看作一阶系统，根据
=G（s），定义
式中，L（s）=αI/（s+α），α为设计参数。
联系上式，可得内模控制器为
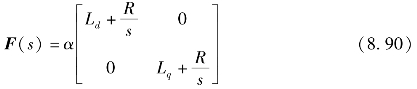
进而可以得到
于是，控制器的调节参数从两个缩减为一个，减小了参数调节的难度，且满足如下关系：
定义响应时间tres为系统响应从阶跃的10%到90%所需的时间，则α与tres的关系近似为tres=ln9/α。由α与tres的关系可知，减小α 将延长系统响应时间，增大α 将加快系统响应速度。但是α不能无限增大，实际中系统响应时间受电气时间常数的限制，电动机的时间常数为
仿真中，电动机参数设置如下：极对数pn=1，定子电感Ld=Lq=0.16 mH，定子电阻R=1.13Ω，磁链ψf=0.007 83Wb，转动惯量J=5.9×10-7kg·m2。仿真条件设置为：直流侧电压Udc=12V，PWM开关频率fpwm=10 kHz，采样周期Ts=10 μs。
由于电流环带宽与电动机的时间常数有关系，即时间常数τ=min｛Ld/R，Lq/R｝，带宽α=2π/τ，根据电动机参数可以计算得到α=44 375 rad/s，从而根据内环电流环的PI参数计算推导式得到PI参数。另外，选取转速环的带宽为β=100 rad/s，将电动机的参数代入外环转速环PI调节器的计算公式，可以得到转速环PI控制器的参数为Ba=0.003，Kpω=0.005，Kpi=0.5。
有关小型转子发动机数值建模与仿真分析的文章
- 详细阅读
-
直接转矩控制方法优化改进详细阅读
直接转矩控制估计定子磁链，由于定子磁链的估计只牵涉到定子电阻，因此对电动机参数的依赖性大大减弱了。直接转矩控制采用了转矩反馈的砰-砰控制，在加减速或负载变化的动态过程中，可以获得快速的转矩响应。图2-10给出了直接转矩控制的原理框图。直接转矩控制系统分别控制异步电动机的转速和磁链。......
2023-06-19
-
直接转矩控制系统优化详细阅读
按定子磁链控制的直接转矩控制系统的原理框图如图7-6所示。图7-6直接转矩控制系统结构示意图直接转矩控制系统中的核心问题是：转矩和定子磁链观测模型以及如何根据转矩和磁链的偏差信号来选择电压空间矢量控制器的开关状态。直接转矩控制系统有以下几个主要特点。也正是由于这个原因，抑制转矩脉动、提高低速性能便成为改进原始的直接转矩控制系统的主要方向，许多学者和开发工程师都在这些性能的改进方面做了大量的研究工作。......
2023-06-25
-
直接转矩控制系统的工作流程优化详细阅读
若转速发生波动使ω<ω，则ASR输出Te增加，T，，由表5.3，这时不插入零矢量，使定子磁链继续旋转，转矩角θ增加，电动机转矩增加，转速ω上升，从而克服转速的波动。若电动机制动和反转，则ω为0或“-”，ASR输出Te极性变“-”，转向信号P/N=0，电压矢量变为反转矢量，控制定子磁链Ψs反向旋转，θ迅速减小，转矩减小，转速下降，电动机制动。......
2023-06-19
-
气隙磁场定向与转矩控制技术优化详细阅读
图6.13 同步电动机空间矢量关系1.气隙磁场定向不考虑阻尼绕组的同步电动机空间矢量关系如图6.13所示。图6.13中建立了两个旋转直角坐标系，其中dq坐标系的d轴与转子励磁Ψf方向重合，mt坐标系的m轴与气隙磁链Ψδ方向重合，即按气隙磁链Ψδ方向定向。定子电流is在mt坐标系轴上投影分别为ism、ist，励磁电流在mt坐标系轴上投影分别为ifm、ift。......
2023-06-19
-
基于电机转矩的动态补偿控制策略优化方案详细阅读
本节将基于理论分析阐述输出转矩波动产生的原因，并提出电机转矩动态补偿的控制方法，实现降低输出转矩波动的目的。因此，如何消除瞬态分量对输出转矩波动的影响，是制动器分离阶段控制策略的主要目标。......
2023-06-24
-
电动机控制环节优化方案详细阅读
松开SB2，虽然其自动复位，但KM线圈继续通电，电动机M连续运行实现长动控制。图2-47 单向长动控制电路为避免电动机等电器和操作者受到不正常工作状态的有害影响，使机床动作更可靠，控制电路均增设有保护环节。利用接触器KM2将电动机M的三相电源进线中任意两相对调，可以实现电动机M的反转控制。......
2023-06-23
-
异步电动机软启动器的优化方案详细阅读
传统的降压启动方式有-△降压启动和自耦变压器降压启动，其启动过程是分级进行，且存在二次冲击，正逐渐由带电流闭环控制的异步电动机软启动器所取代。图5.21 给出了软启动器的几种启动方式。图5.21为点动启动方式，在这种方式下，软启动器的输出电压迅速增加到点动电压（可设定）并保持不变，这种方式对试车和负载定位非常方便。......
2023-06-23
相关推荐