=f=e0=1，f（n+1）（θx）=eθx.故f=ex的n阶麦克劳林公式为例2 求f=sinx的带有拉格朗日型余项的n阶麦克劳林公式.解 ，所以f=0，f′=1，f″=0，f=-1，f=0，…从而其中，例3 求.解 ，，所以原式.几个常用函数的麦克劳林公式：由以上带有佩亚诺型余项的麦克劳林公式，易得相应的带有拉格朗日型余项的麦克劳林公式，读者可自行写出.......
2023-11-22
公式比较：与其他公式对比
【摘要】：下面就基于通用水流功率概念建立的输沙能力公式与常用的Engelund-Hansen公式、Ackers-White公式、Yang公式以及Toffaleti公式进行比较。Engelund-Hansen 公式是公认的比较可靠的公式之一，在实际中得到了广泛应用。考虑到Toffaleti的输沙率公式主要是依据大河流的资料建立的，本节的比较也包括了该式在内。对于414组大河流的资料，公式和Toffaleti方法得到的计算与实测含沙量之间的平均偏差比R分别为1.14和1.19，Engelund-Hansen公式和Ackers-White公式的平均偏差比R分别为2.21和1.65。
过去对于水流输沙能力问题已有大量的研究，很多作者依据不同的理论模式和资料建立了众多的输沙能力公式，其适用范围和精度也各不相同。为了满足实际应用的需要，曾有不少作者依据实测输沙资料对一些常见的输沙能力公式进行了比较，例如White等(1975)、Alonso(1980)、Brownlie(1981a)、American Society of Civil Engineers(1982)、Yang 和Molinas(1982)、Vetter(1988)以及Yang和Wan(1991)的研究。下面就基于通用水流功率概念建立的输沙能力公式(2-19)与常用的Engelund-Hansen(1967)公式、Ackers-White(1973)公式、Yang(1973)公式以及Toffaleti(1968)公式进行比较。
Engelund-Hansen (1967)公式是公认的比较可靠的公式之一，在实际中得到了广泛应用。该公式的建立主要是基于Bagnold (1966)的水流功率理论和相似性原理，其推导过程具有一定的理论基础。公式中有关参数的率定所依据的资料为Guy等 (1966)的116 组实验室水槽试验资料，包括的泥沙粒径为0.19mm、0.27mm、0.45mm 和0.93mm，最大水深0.34m。Ackers-White(1973)基于可动性理论和Bagnold (1966)的水流功率概念建立了一个具有一定理论基础的床沙质输沙能力公式。公式中的参数A、C、m 和n 则是根据水深小于0.4m、泥沙粒径由0.04～4.0mm 的925组实验室水槽资料确定的。Yang (1973)公式是基于单位水流功率理论建立的。公式中的系数和指数是依据463组实验室水槽资料确定的，其相应水深为0.022～0.86m，泥沙粒径的变化范围为0.137～1.35mm。
上述3个公式都是基于能量概念建立的。考虑到Toffaleti(1968，1969)的输沙率公式主要是依据大河流的资料建立的，本节的比较也包括了该式在内。Toffaleti参考Einstein (1950)及Einstein 和Chien (1953)的概念，假定推移质泥沙的输移发生在一个很薄的床面层内，该床面层的含沙量便是计算悬移质输沙率的参考含沙量。首先把整个水深分为4个区，即床面层、下区、中区和上区，规定了每一层的相对厚度，并给出了每一层相应的流速分布和含沙量分布公式，然后对每个区域进行积分得到相应的单宽输沙率。Simons和Sentürk (1992)、Shen (1979)、Yang (1996)均建议，Toffaleti方法可以用于大河流的输沙能力计算。
采用上述4个公式及本节建立的公式，对414组大河流资料和534组中等河流资料的输沙能力进行了计算，各公式计算结果与实测含沙量的比较见表2-2和表2-3。
表2-2 大河流的计算床沙质输沙能力与实测床沙质含沙量的比较
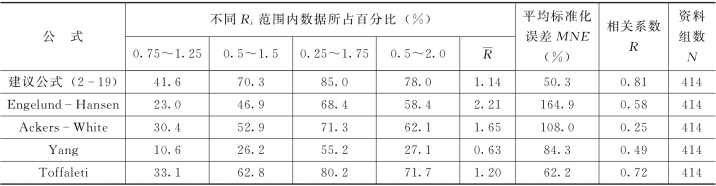
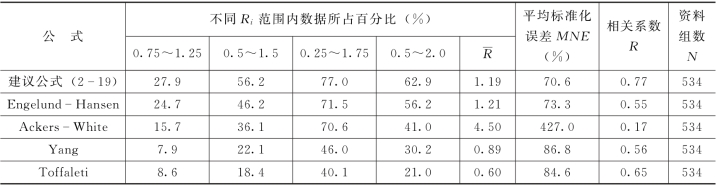
表2-3 中等河流的计算床沙质输沙能力与实测床沙质含沙量的比较
所采用的统计参数包括:
(1)偏差比(discrepancy ratio)
(2)平均偏差比(mean discrepancy ratio)
(3)平均标准化误差(mean normalized error)
(4)相关系数(correlation coefficient)
式中:下标c代表计算值;下标m 代表实测值;上横杠表示平均值;i为资料编号;N 为资料组数。
对于414组大河流的资料，公式(2-19)和Toffaleti方法得到的计算与实测含沙量之间的平均偏差比R分别为1.14和1.19，Engelund-Hansen公式和Ackers-White公式的平均偏差比R分别为2.21和1.65。这一结果说明，就平均而言，Engelund-Hansen公式和Ackers-White公式计算的输沙能力均偏大。关于Engelund-Hansen公式，Posada(1995)的研究也曾发现，当Engelund-Hansen公式用_于大水深河流时给出的计算值偏大，大约是实测值的2 倍。Yang 公式的平均偏差比R 为0.63，说明就平均而言，Yang公式计算的输沙能力偏小。
偏差比Ri代表了计算与实测含沙量之间的误差分布情况。表2-2列出的偏差比表明，在比较的5个公式中，公式(2-19)的表现最好。公式(2-19)、Engelund-Hansen公式、Ackers-White公式、Yang公式及Toffaleti方法给出的计算与实测含沙量之间的平均标准化误差分别为50.3、164.9、108.0、84.3、62.2，相关系数分别为0.81、0.58、0.25、0.49、0.72。平均标准化误差和相关系数均表明，对于大河流而言，式(2-19)得到的计算与实测含沙量之间的符合程度最好，Toffaleti方法给出的计算结果次之。
为了验证公式(2-19)的适用性，需要对其进行独立的检验。考虑到只有414组大河流的输沙资料，组数有限，这里采用534组中等河流的输沙资料(见表2-1)对式(2-19)进行了独立的检验，相应的计算床沙质输沙能力与实测床沙质含沙量之间的比较结果见表2-3。公式(2-19)、Engelund-Hansen公式、Ackers-White公式、Yang公式及Toffaleti方法给出的计算与实测含沙量之间的平均偏差比分别为1.19、1.21、4.50、0.89、0.60，平均标准化误差分别为70.6、73.3、427.0、86.8、84.6，相关系数分别为0.77、0.55、0.17、0.56、0.65，此外，偏差比Ri落在0.25～1.75 范围内的数据点的比例分别为77.0%、71.5%、70.6%、46.0%、40.1%。这些统计参数均表明，对于中等河流而言，本节提出的公式的预报精度最高，Engelund-Hansen公式次之，而Toffaleti方法给出的预报结果最差。由于Toffaleti方法是基于大河流资料建立的，在这里表现不佳是可以理解的。
图2-5 给出了采用Engelund-Hansen 公式、Ackers-White公式、Yang 公式及Toffaleti方法，对414组大河流资料的计算与实测含沙量之间的比较，图2-6给出了对534组中等流资料的计算与实测含沙量之间的比较，图2-7则是公式 (2-19)的计算与实测含沙量之间的比较。可以看到，无论大河流还是中等河流，公式 (2-19)给出的计算结果与实测值之间的符合程度均为最好。
图2-5 414组大河流资料的计算与实测含沙量的比较
(a)Engelund-Hansen公式;(b)Ackers-White公式;(c)Yang公式;(d)Toffaleti方法
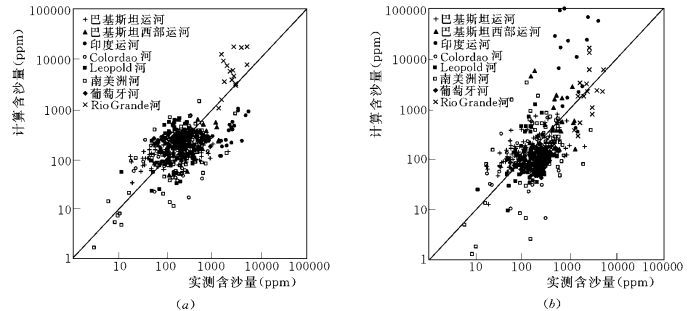
图2-6 534组中等河流资料的计算与实测含沙量的比较 (一)
(a)Engelund-Hansen公式;(b)Ackers-White公式
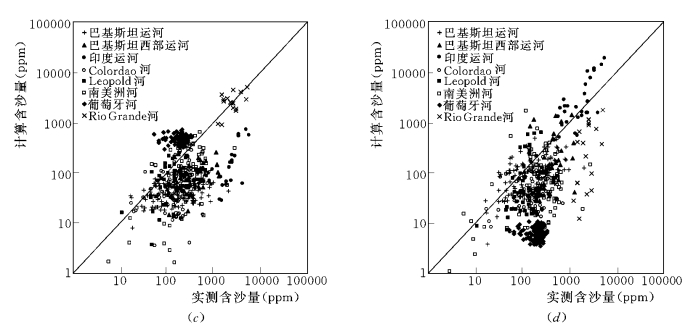
图2-6 534组中等河流资料的计算与实测含沙量的比较 (二)
(c)Yang公式;(d)Toffaleti方法
图2-7 式 (2-19)计算与实测含沙量的比较
(a)414组大河流资料;(b)534组中等河流资料
有关泥沙研究进展的文章
- 详细阅读
-
大河流输沙能力公式详细阅读
Einstein 认为，水流的输沙能力与水流克服沙粒阻力所要求的能坡J′有关，而不是总能坡J。式表示的关系式与Velikanov、张瑞瑾、窦国仁分别提出的式 (2-2)、式(2-4)、式(2-5)表示输沙能力关系的形式基本相同。因此，在大河流的输沙能力计算公式中，选择合适的阻力公式，将比降表示为速度和水深的函数，是一种较为有效的处理办法。根据表2-1给出的414组大河流输沙资料点绘了Ct与Ψ 的关系，见图2-4。......
2023-06-22
-
条件概率、乘法公式、全概率公式、贝叶斯公式解详细阅读
，Bn两两互不相容，且满足B1∪B2∪…∪Bn=Ω），则当P>0（i=1，2，…，n）时，对任意事件A有注 使用全概率公式解题时，可按以下原则寻找完全事件组B1，B2，…，Bn都较A先发生.贝叶斯公式：设B1，B2，…精解 先引入有关事件：A1={甲表演}，A2={乙表演}，A3={丙表演}，B={一次命中一次未命中}，则由于B与A1，A2，A3有关，且A1，A2，A3是发生于B之前的一个完全事件组，因此由全概率公式得所以......
2023-10-27
-
推导推移质公式详细阅读
推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比......
2023-06-22
-
对流换热的经验公式详细阅读
在太阳能利用系统的分析设计中，为了计算对流换热量，必须要知道牛顿冷却公式中的对流换热系数h。所以，一般我们将对流换热的实验数据整理成各无量纲数之间的关系式，以供在集合上与之相似的流动边界条件使用。因此，在确定实际问题中的对流换热系数时，必然会使用到如式和这样的准则公式。......
2023-06-23
- 详细阅读
-
水流输沙能力公式的修正方法详细阅读
由此可见，含沙量对水流输沙能力的影响是十分显著的，是造成多沙河流输沙能力不同于少沙河流的重要因素。为了解决生产中所提出的问题，不得不依赖于一些经验性输沙能力公式。......
2023-06-22
-
计算公式的分析与讨论详细阅读
分析认为对于较小的等标污染负荷，水库岸边污染混合区相对较窄，涉及水深较浅，污染物比较容易达到垂向混合均匀，所以这时污染混合区范围出现与二维理论求解得到的解析计算公式变化规律相同的情况；对于较大的等标污染负荷，水库岸边污染混合区相对较宽，涉及水深较大，污染物不容易达到垂向混合均匀，所以这时污染混合区范围出现与本文三维理论求解得到的解析计算公式变化规律相同的情况。......
2023-06-26
相关推荐