(一)概念综合评价就是运用多个指标对评价对象进行评价,以得出综合性结论的方法。......
2023-07-22
发展服务外包产业,在解决我国大学生就业、为中高级技术人员提供创新平台,在中国经济结构调整、转型升级、持续发展中发挥独特作用,已得到社会各界的认同。由于服务外包产业在我国起步较晚,各项基础工作如发展规划、扶持政策、基础设施、行业相关标准以及有关产业边界的划分、统计数据的归类等正在逐步完善中。所以在数据来源有限的前提下,为较合理和科学地评价服务外包示范城市、专业园区以及领军企业在服务外包产业发展方面的实际情况,使其更好地发挥示范和引领作用,带动我国服务外包产业又快又好发展,显得很有必要。
在综合评价方法中,常用的方法是根据指标的设定、数据收集和标准化处理后的功效值计算,最后运用一般综合评价指数计算方法,较为科学地计算出每个被评城市、机构和企业的具体得分。在这些步骤中,重要的环节是由于指标的重要性程度不一样,数据来源的信息量也不相同,对每个指标应赋予不同的权重来表示各个指标在评价中的作用,使得评价结果更为客观。本文对权重的常用赋值方法,结合我国服务外包产业发展现状进行一些探索。
一、权重赋值方法
确定综合评价中的各指标权重,根据数据的容量,一般常用的有主观赋权法、因子分析法和层次分析法。
(一)主观赋权法(Delphi法)
通过广泛集中有实践经验的专家意见,根据专家意见形成各评价指标的权数。主观赋权法常适用于指标容量(业内也常称“跑量”)有限的情况下的综合评价。
主观赋权法一般采用匿名发表意见的方式,即专家之间不互相讨论,不发生横向联系,只能与调查人员发生关系,通过多轮次调查专家对问卷所提问题的看法,经过反复征询、归纳、修改,最后汇总成专家基本一致的看法,作为预测的结果。但专家“专”的程度和对项目或指标的理解程度是工作中的难点。(具体工作步骤略)
(二)因子分析法
依据评价指标提供的数据,计算各指标数据之间的方差和相关程度,若同一指标能提供较多时期(或五年以上)的数据,用因子分析法比较科学简便。因子分析法的原理主要采用数理方法中相关系数的计算来确定各个指标对综合指标的贡献,确定相应的权数。相关系数,或称皮氏积矩相关系数(Pearson productmoment correlation coefficient),它由英国统计学家卡尔·皮尔森(Karl Pearson)在19世纪80年代提出的。两指标之间的相关系数越接近1,说明这两个指标高度相关,也即重复信息程度很高,在综合评价中的作用会很小,于是取对应的权数可越小。相关系数越接近0,说明相关程度很薄弱,也即重复信息程度很小,在综合评价中的作用就越大,因此可取对应权数可越大。
(三)层次分析法(AHP法)
由于主观分析法与专家的业务宽窄有关,而因子分析法与数据来源的容量有关,两个方法都会受到一些牵制。层次分析法就是主观分析法+因子分析法。
层次分析法(Analytic Hierarchy Process)简称AHP,是美国运筹学家T.L.Saaty教授于70年代初期提出的,它的特点是把各种因素通过划分为相互联系的有序层次,使之条理化,根据对一定客观现实的主观判断结构(主要是两两比较)把专家意见和分析者的客观判断结果直接而有效地结合起来,将每个层次元素两两比较的重要性进行定量描述。而后,计算反映每一层次元素的相对重要性次序的权值,通过所有层次之间的总排序计算所有元素的相对权重并进行排序。
层次分析法适用于各指标间存在层次关系,或者有明显的类别划分,同时各指标对最终评价的影响程度无法直接通过足够的数据进行量化计算的时候,就可以选择使用层次分析法。
二、因子分析法中的权数计算
(一)相关系数的计算
用rxy表示指标X和Y的相关系数:设指标X和Y分别由n个数据组成的序列(如时间序列等),记为
X=(x1、x2、…、xn),Y=(y1、y2、…、yn)
σxy为X和Y是两个指标数列的协方差(Covariance);
σx和σy分别为指标数列X和Y的标准差(Standard Deviation);则相关系数
![]()
式中:
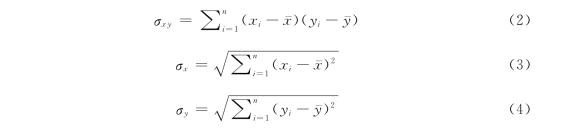
这里均值
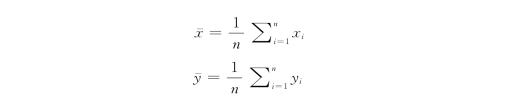
于是式(1)可表示为
![]()
由于![]() 和
和![]() 计算中会产生许多小数点,使得整个运算较为复杂化,上式又可 简化为以下公式(具体证明见后):
计算中会产生许多小数点,使得整个运算较为复杂化,上式又可 简化为以下公式(具体证明见后):
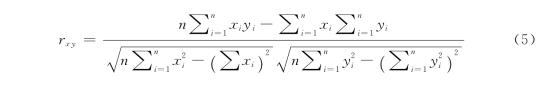
可以证明
![]()
一般当|rxy|≤0.3时,称低度相关。
例1 相关系数计算。假设已获得某城市5年(n=5)的离岸服务外包合同执行额为x,实缴各类税收金额为y。具体数据和计算过程见表1。
表1
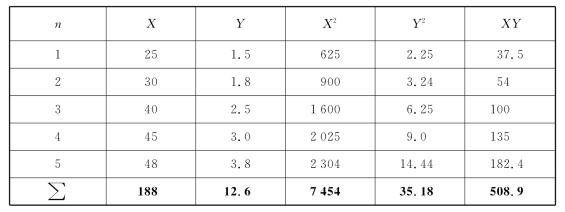
将上表的相关数据代入式(5),得

数字表明,离岸合同执行金额与实缴各类税金这两个指标高度相关。
式(1)中σxy为x和y是两个指标数列的协方差,若有m个指标,就需要计算![]() 个协方差(因rij=rji,i,j=1,2,…,m)。在具体应用中,一般都根据上述原理,用SPSS软件来计算指标间的相关系数。
个协方差(因rij=rji,i,j=1,2,…,m)。在具体应用中,一般都根据上述原理,用SPSS软件来计算指标间的相关系数。
(二)权数的赋值(www.chuimin.cn)
上述仅是两个指标的相关系数的计算,若有m个指标,则所有两两不同指标间的相关系数,就可表示为以下矩阵:

上述R称为相关系数矩阵,显然R是一个对称矩阵rij=rji,其对角线rii取值均为1,表示自相关系数。将R中的负相关系数以0代替,然后按列求和,这样可得出指标i与其他(M-1)个指标的相关系数的和组成的行向量
![]()
为运算简化起见,一般都再把(7)再进行归一化处理,这样就可以得出对应各指标的权数。
比如,评价体系中一级指标为“产业情况、基础设施情况、人才培养培训与就业、政策措施、行业特色”,根据收集近五年的数据,经过SPSS软件计算出相关系数,将组成相关系数矩阵R的各列数字相加的和,根据指标的排列次序得出以下行向量:
(1.45,0.76,0.74,0.65,0.4)
将其归一化后再乘以1 000,得出“产业情况、基础设施情况、人才培养培训与就业、政策措施、行业特色”五个指标对应的权数是
(360,190,190,160,100)
例2 指标权数的计算。假设对若干个城市开展服务外包产业的综合评价,经过各地商务主管和相关部门对近五年的10个方面指标,由统计部门审核后上报的数据,经过核查确认以及对此10个指标进行两两相关系数的计算,得出相关系数矩阵R,将R各列相加后获得的10个数字,即对应了10个指标间相关系数的和,组成如下行向量:
(5.81,3.32,7.11,3.12,6.01,2.22,8.57,9.86,4.92,1.48)
归一化后,变为
(0.11,0.06,0.15,0.05,0.11,0.04,0.16,0.20,0.09,0.03)
为评价中计算方便起见,归一化后的向量再乘1 000,于是就得出10个指标对应的权数应是:
(110,60,150,50,110,40,160,220,90,30)
本文小结:
以上对三种权数赋值方法进行介绍,并对因子分析法中权数的计算方法进行分析探讨,但需说明
(1)因子分析法中相关系数仅是描述不同指标间的相关程度,而与具体指标的单位没有关系。
(2)因子分析法中当数据采集时间的年份数n(也称数据容量)较小时,相关系数的波动会较大,相关性的判断不很明显,此时有些数据的相关系数绝对值容易偏大;当n较大时,相关系数的绝对值容易偏小,相关性的判断会比较明显。因此在数据容量n较小时,我们仅凭相关系数较大就判定变量两个指标之间有密切的相关程度就显得欠妥的。
(3)根据我国目前服务外包发展较快和产业统计现状正在逐步完善中的现状,在对示范城市综合评价中对指标权数的确定,建议用主观赋权法较适宜。若条件成熟,可以用因子分析法来验证,使得权数更为客观确切。
附:关于简化的相关系数计算公式的推导
rxy=σxy/σxσy
![]()
其中协方差
![]()
方差

均值
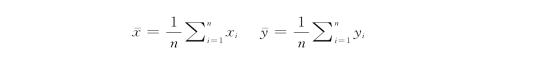
将式(Ⅲ)、式(Ⅳ)代入式(Ⅱ),为简便起见,下面![]() 简记为∑
简记为∑


同理,

将式(8)、式(9)、式(10)代入式(1)
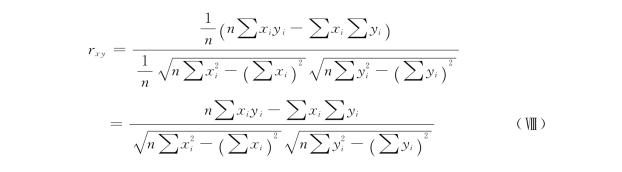
2013年5月28日
有关中国服务外包产业研究与实践的文章

在目前的教师信息素养量化研究中,普遍以两个级别区分不同内容的评价指标。其次是学校、区域教育信息化程度不均衡的影响。在我国教育信息化程度较低的区域,教师人均电脑保有量不足一台,月均上网次数不足一次。此外,即使是在较为发达的区域,不同学校之间的教育信息化程度也存在较大差异。同样,在我们以二级指标量化教师信息素养水平时,也要在符合我国教育信息化的发展现状的同时,做到与时俱进。......
2023-11-25

在沙漠公路路面使用性能评价中,所用的路面使用性能评价指标就是上述六个,目前尚处于探索阶段,有理由认为可能存在没有被用到但很关键的指标,因此,进行灰色理论分析是可行的。在沙漠公路路用性能评价中,评价指标越不均衡,用规范评价方法得出的结果越不可靠。表6-38 阿和沙漠公路路面性能综合评价结果......
2023-09-22

基于水体被有机物污染是很普遍的现象,该指标也作为有机污染物相对含量的综合指标之一,但只能反映能被氧化剂氧化的有机污染物。测定化学需氧量的标准方法是重铬酸钾法。电解液为10.2mol/L硫酸、重铬酸钾和硫酸铁混合液。mol/L重铬酸钾溶液进行标定值测定时,最低检出质量浓度为3mg/L;测定上限为100mg/L。但是,只有严格控制消解条件一致和注意经常清洗电极、防止沾污,才能获得较好的重现性。市场上有多种这类快速COD测定仪出售。......
2023-11-23

泸州市义务教育阶段学生综合素质评价指标框架是基于教育部《中小学教育质量综合评价指标框架(试行)》而研发编制的。分小学低段、中段、高段,初中段制定发展性评价标准。泸州市教委还根据实际情况对二级指标和三级指标进行了一些调整。学业负担状况通过采集家长、教师和学生问卷数据,进行数据分析得到结果。......
2023-07-18

静态分析问题解决只有最后的一个结果,根据解题者达到目标的程度给予满分或部分评分。所以动态问题解决或复杂问题解决可以分别评价知识获取和知识应用两个阶段的结果。尽管后面四种方法没有因果关系图那么常用,但是问题解决者会意识到他们被问到的是获得外显的结构性知识。......
2023-10-19

教育科学中的“情意领域”是指除认知领域和动作技能领域以外的和情感联系比较紧密的那些学习变量,如兴趣、动机、态度等。从某种意义上来说,情意领域与我国课程改革标准中的“情感、态度与价值观”刚好对应。可见,情意领域的评价研究刻不容缓。......
2023-11-29

例如,当阻尼比减小,车身固有频率及轮胎和悬挂的刚度比都增大时,加速度将增大,这说明车身振动较为剧烈,这恰恰是因为所设计的悬挂系统未能更好地衰减路面不平激励所带来的冲击,从而导致了振动的加剧;反之当悬挂系统的性能下降时,加速度也会增大,振动加剧。车体的阻尼比、频率比、悬挂刚度比,以及车体和车轮的质量比发生变化,会影响到整个系统的性能参数,进而引起轮胎动载荷发生变化。......
2023-06-24
相关推荐