【摘要】:定义9.3 设n阶方阵定义矩阵A的行列式为其中的和号∑是对所有的n级排列j1j2…in,从而由前面的推论9.1知.由此可得:定理9.2n阶方阵A的行列式可定义为其中的和号∑是对所有的n级排列i1i2…jn均为n-排列,证明:在n阶行列式的定义中,项的符号是.
定义9.3 设n阶方阵
定义矩阵A的行列式为
其中的和号∑是对所有的n级排列j1j2…jn的总共n!项求和.
A是n阶矩阵时,A的行列式也称为n阶行列式.上述定义表明,n阶行列式等于所有不同行不同列的n个元素乘积的代数和,其符号在行下标为自然顺序排列的情况下,由列下标排列的逆序数来确定.
例9.5 计算四阶方阵
的行列式|A|.
解:这是一个四阶行列式,其值应为24项乘积的代数和.但由于A有很多的元素为零,容易看到乘积不为零的项只有一项a14a23a32a41.又由于τ(4321)=6,所以该项的符号为正,因此|A|=24.
对于n阶行列式中的任意一项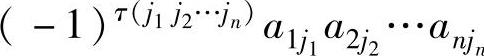 ,对换上述乘积中两元素的位置,不改变其积.但可以将列下标排为自然顺序,即有(www.chuimin.cn)
,对换上述乘积中两元素的位置,不改变其积.但可以将列下标排为自然顺序,即有(www.chuimin.cn)
当列下标排列j1j2…jn经若干次对换,变为自然顺序排列时,通过同样的对换,行下标由自然顺序排列变为i1i2…in,从而由前面的推论9.1知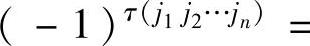
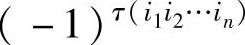 .由此可得:
.由此可得:
定理9.2n阶方阵A的行列式可定义为
其中的和号∑是对所有的n级排列i1i2…in求和.
习题
9.3.1. 利用行列式的定义计算下列行列式的值.
9.3.2. 利用行列式的定义证明:
9.3.3. 若i1i2…in与j1j2…jn均为n-排列,证明:在n阶行列式的定义中,项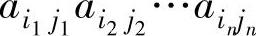 的符号是
的符号是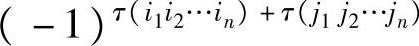 .
.

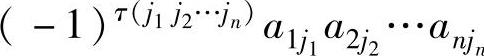 ,对换上述乘积中两元素的位置,不改变其积
,对换上述乘积中两元素的位置,不改变其积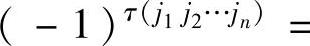
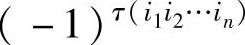
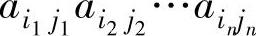 的符号是
的符号是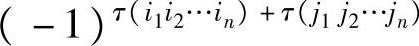








相关推荐