我们知道,光是沿直线传播的.物体在光线的照射下,会在不透明物体后面的屏幕上(如墙面或地面等)留下这个物体的影子(见图3-39),这种现象就叫做投影.其中,把光线叫做投影线,把留下物体影子的屏幕叫做投影面.图3-39(1)中心投影把光由一点向外散射所形成的投影,叫做中心投影(见图3-40).中心投影的投影线交于一点,即投射中心.中心投影现象普遍存在于我们的生活中.例如,舞台灯、路灯、手电筒和台灯的光......
2023-11-22
知识回顾
如果一个数的平方等于a,那么这个数叫做a的平方根.一个正数有两个平方根;0只有一个平方根,它是0本身;负数没有平方根.
,有两个外观
完全相同的用电器,甲的电阻为15Ω,乙的电阻为30Ω,现测得某用电器的功率为1500W,两端电压在200V至250V之间,该用电器到底是甲还是乙?
解:根据已知条件P=1500W,R甲=15Ω,R乙=30Ω,代入公式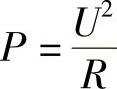
得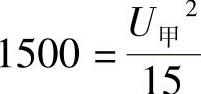
所以该用电器应该是乙.
练一练
1.求出下列各数的平方根:(1)64;(2)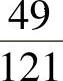
;(3)0.0004;(4)(-25)2;(5)11.
例7 化简:
解:
例8 化简:
(1) ; (2)
; (2)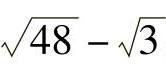 ; (3)
; (3)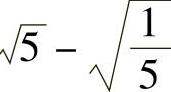
.
解:
一般地,若xn=a(n>1,且∈N+),我们把x叫做a的n次方根.
当n是奇数时,任何一个数的n次方根都唯一存在,且正数的n次方根是一个正数,负数的n次方跟是一个负数.这时,a的n次方根用符号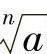
表示.
例如,因为23=8,所以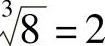 ;因为(-2)5=-32,所以
;因为(-2)5=-32,所以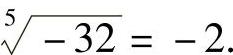
当n是偶数时,正数的n次方根有两个,它们互为相反数,分别表示为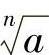 和
和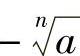 ,也可以合并写为
,也可以合并写为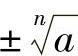 (a>0).
(a>0).
例如,因为24=16,(-2)4=16,所以16的四次方根有两个,即2或-2,可表示为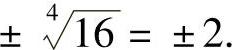 (www.chuimin.cn)
(www.chuimin.cn)
零的任何次方根都是零,记作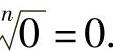
正数a的正的n次方根叫做a的n次算术根.
例如,2叫做16的4次算术根.
例9 求值:
(1)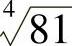 ; (2)81的4次方根.
; (2)81的4次方根.
解:(1)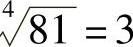 ;
;
(2)81的4次方根有两个,即3或-3.
当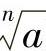 有意义时,式子
有意义时,式子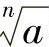 叫做n次根式,其中n叫做根指数,a叫做被开方数.
叫做n次根式,其中n叫做根指数,a叫做被开方数.
练习
1.填空题.
2.求值:
(1)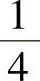 的平方根; (2)243的5次方根; (3)256的4次方根.
的平方根; (2)243的5次方根; (3)256的4次方根.
3.自由下落物体下落的距离s(m)与下落时间t(s)的关系为s=4.9t2,有一铁球从19.6m高的建筑物上自由下落,到达地面需要多长时间?
习题二
1.计算题.
2.填空题.
10000=10( ),16=2( ),1000=10( ),8=2( ),
100=10( ),4=2( ),10=10( ),2=2( ),
1=10( ),1=2( ),0.1=10( ),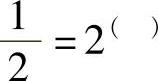
,
0.01=10( ),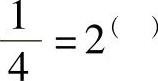
,0.001=10( ),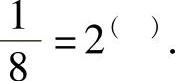
有关机电应用数学的文章

我们知道,光是沿直线传播的.物体在光线的照射下,会在不透明物体后面的屏幕上(如墙面或地面等)留下这个物体的影子(见图3-39),这种现象就叫做投影.其中,把光线叫做投影线,把留下物体影子的屏幕叫做投影面.图3-39(1)中心投影把光由一点向外散射所形成的投影,叫做中心投影(见图3-40).中心投影的投影线交于一点,即投射中心.中心投影现象普遍存在于我们的生活中.例如,舞台灯、路灯、手电筒和台灯的光......
2023-11-22

1.椭圆的定义做一做取一条一定长的细绳,把它的两端固定在画图板上的F1和F2两点,当绳长大于F1和F2的距离时,用铅笔尖把绳子拉紧,使笔尖在图板上慢慢移动,请同学们利用手中绳子配合同桌共同完成,看看可以得到什么图形.图4-18议一议在画图的过程中,哪些量发生了变化?......
2023-11-22

回顾与思考初中学过的数,它们的关系可以归纳如下:议一议有理数和无理数有什么区别?数的集合简称数集,全体非负整数的集合,通常简称非负整数集,记作N,非负整数集内排除0的集合,也称正整数,记作N+;全体有理数的集合,简称有理数集,用Q表示;全体实数的集合,简称实数集,用R表示.为了方便,还用Q+表示正有理数集,Q-表示负有理数集;R+表示正实数集,R-表示负实数集.我们通常用大写拉丁字母A,B,C,…......
2023-11-22

由正弦函数y=sinx的图像可知:定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx,x∈R的值域是[-1,1],即对任意的x∈R,都有-1≤sinx≤1.其中,当,k∈Z,有ymax=1;当,k∈Z时,有ymin=-1.想一想等式2sinx=3,,都成立吗?例2求出下列函数的最大值和最小值:y=1-sinx; y=2sinx.解:当sinx=-1时,ymax=1-(-1)=2;当sinx=1时,ymin=1-1=0.当sinx=1时,ymax=2×1=2;sinx=-1时,ymin=2×(-1)=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时,对应的x的取值集合分别是什么?......
2023-11-22

在实际的生产和生活中,我们经常遇到的并不是简单的几何体,而是由一些简单几何体构成的组合体.对于组合体,一定要认真观察,先弄清楚它的基本结构,然后再画它的三视图.试一试如图3-51所示的组合体,它是由哪些简单几何体组合而成的?你能画出它的三视图吗?......
2023-11-22
相关推荐