,Cn是n个独立的任意常数)是n阶微分方程的解,则称其为该n阶微分方程的通解.如果由初始条件确定了y=φ(x,C1,C2,…......
2023-10-27
首先研究最简单的一阶微分方程,即可分离变量的微分方程.一、可分离变量的方程
可以化成形如
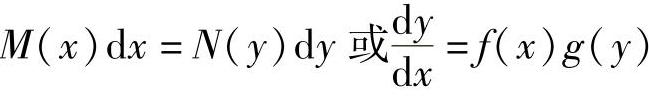
形式的方程称为可分离变量的微分方程.
对M(x)dx=N(y)dy两端分别积分,便得方程的通解:
∫M(x)dx=∫N(y)dy+C(C是任意常数).
例1 求方程(1+y2)dx-x(1+x2)ydy=0的通解.
解 用x(1+x2)(1+y2)除方程两边整理得
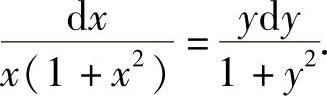
两边积分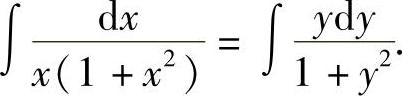
因为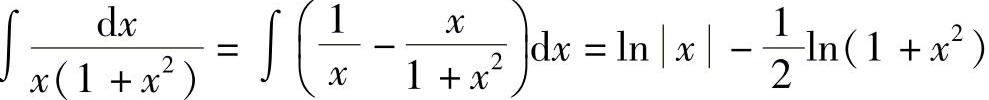 ,
,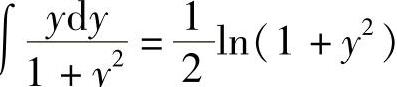 ,
,
所以
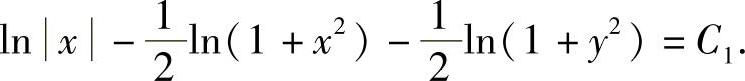
即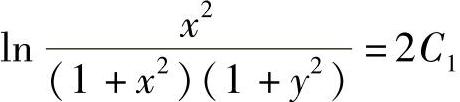 ,或
,或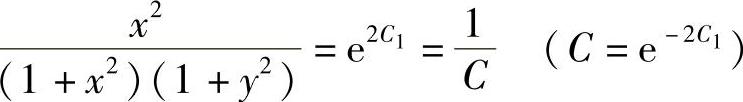 ,
,
通解为(1+x2)(1+y2)=Cx2.此外方程还有解x=0.
例2 设推广某项新技术时,需要推广的总人数为N,t时刻已掌握技术的人数为P(t),新技术推广速度与已推广人数和待推广人数成正比,即有微分方程
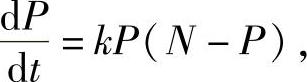
其中,k为比例常数(此方程称为自我抑制性方程也叫逻辑斯蒂增长模型,它是经济学中常遇到的数学模型),试求解该微分方程.
解 将该方程变形为
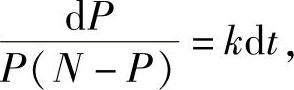
两边积分得
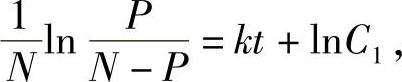
整理得通解
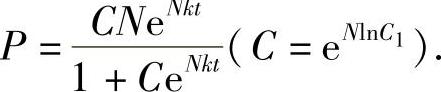
例3 某公司t年净资产有W(t)(单位:百万元),并且资产以每年5%的速度连续增长,同时该公司每年要以30(百万元)的数额连续支付职工工资.
1)给出描述净资产W(t)的微分方程;2)假设初始净资产为W0,求解微分方程;3)讨论在W0=500、600、700这3种情况下,W(t)的变化特点.
解 1)利用平衡法,
即 净资产增长速度=资产本身增长速度-职工工资支付速度得到方程

即
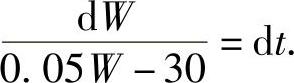
2)对上式两边积分,得
ln|W-600|=0.05t+lnC,于是
|W-600|=Ce0.05t,或
W-600=ae0.05t(a=±C),将W(0)=W0代入,得方程特解
W=600+(W0-600)e0.05t.
在上式推导过程中W≠600,当W=600时,有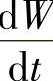
=0,可知W=600=W0,通常称为平衡解,可见平衡解已包含在了通解之中.
3)由通解表达式可知,当W0=500时,净资产额单调递减,公司将在第36年破产;当W0=600时,公司将收支平衡,净资产将保持在600(百万元)不变;当W0=700时,净资产额将按指数不断增长.
例4 设降落伞从跳伞塔下落后,所受空气阻力与速度成正比,并设降落伞离开跳伞塔时(t=0)速度为零,求降落伞下落速度与时间的函数关系.
解 设降落伞下落速度为v(t).降落伞在空中下落时,同时受到重力P与阻力R的作用(见图6-1).重力大小为mg,方向与v一致;阻力大小为kv(k为比例系数),方向与v相反,从而降落伞所受外力为
F=mg-kv.
根据牛顿第二运动定律
F=ma.
(其中a为加速度),得函数v(t)应满足的方程为

按题意,初始条件为
v|t=0=0.

图6-1
方程(6-3)是可分离变量的,分离变量后得
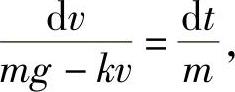
两端积分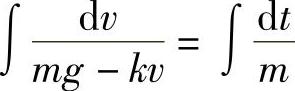 ,考虑到mg-kv>0,得
,考虑到mg-kv>0,得
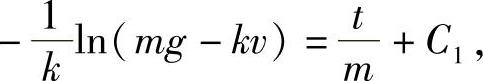
即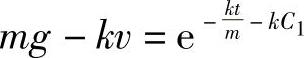 ,或
,或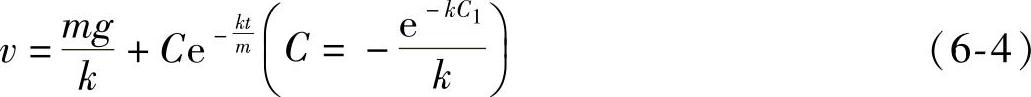 这就是方程(6-3)的通解.
这就是方程(6-3)的通解.
将初始条件v|t=0=0代入式(6-4)得
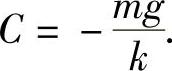
于是所求的特解为
由式(6-5)可以看出,随着时间t的增大,速度v逐渐近于常数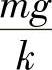 ,且不会超过
,且不会超过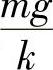 ,即跳伞后开始阶段是加速运动,但以后逐渐接近于匀速运动.
,即跳伞后开始阶段是加速运动,但以后逐渐接近于匀速运动.
例5 有高为100cm的半球形容器,水从它的底部小孔流出,小孔横截面积为1cm2(见图6-2).开始时容器内盛满了水,求水从小孔流出过程中容器里水面的高度h(水面与孔口中心间的距离)随时间t的变化规律,并求水流完所需的时间.
解 由物理学知识可知,水从孔口流出的流量(即通过孔口横截面的水的体积V对时间t的变化率)Q可用下列公式计算:
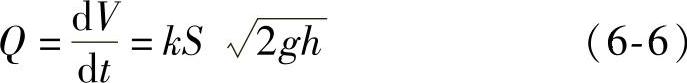
其中,k为流量系数,由实验测得k=0.62,S为孔口横截面的面积,g为重力加速度.
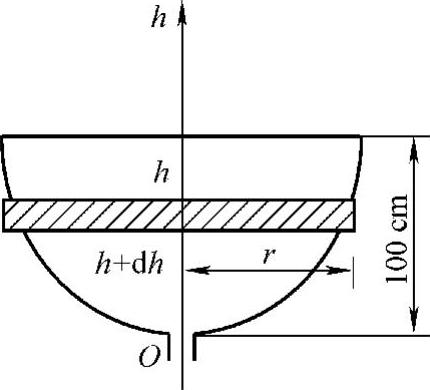
图6-2
另一方面,设在微小时间间隔[t,t+dt]内,水面高度由h降至h+dh(dh<0),则又可得到
dV=-πr2dh (6-7)
其中,r是时刻t的水面半径(见图6-2),等式的右端置负号是由于dh<0而dV>0的缘故.又因为
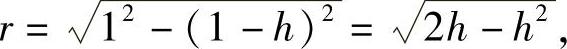
所以式(6-7)变成
dV=-π(2h-h2)dh (6-8)
比较式(6-6)和式(6-8)两式,得
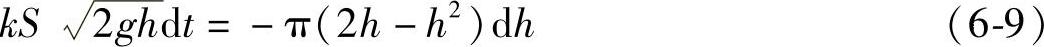
这就是未知函数h=h(t)应满足的微分方程.
此外,开始时容器内的水是满的,所以未知函数h=h(t)还应满足下列初始条件:
h|t=0=1. (6-10)
方程(6-9)是可分离变量的,分离变量后得
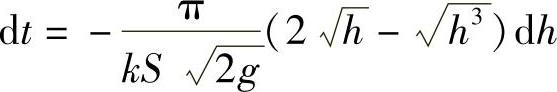
两端积分,得
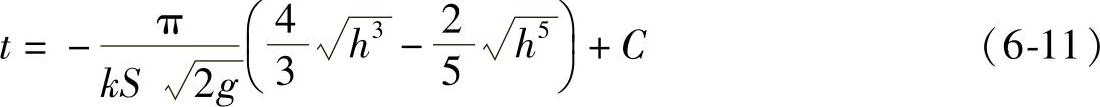
其中,C是任意常数.
把初始条件式(6-10)代入式(6-11),得
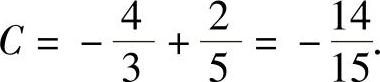
把所得的C值代入式(6-11)并化简,得
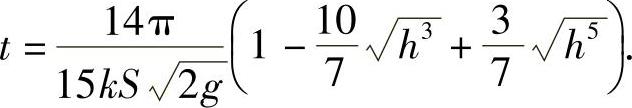
以k=0.62,S=10-4m2,g=9.8m/s2代入上式,计算后可得
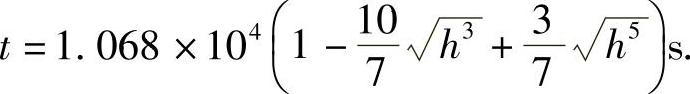
上式表达了水从小孔流出的过程中容器内水面高度h与时间t之间的函数关系.由此可知水流完所需的时间为
t=1.068×104s=2h58min.
这里还要指出,在本例是通过对微小量dV的分析得到微分方程(6-9)的,这种微小量分析的方法,也是建立微分方程的一种常用方法.
二、齐次微分方程
形如
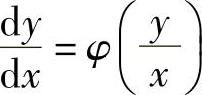
的一阶微分方程称为齐次微分方程.
对方程 作变量代换
作变量代换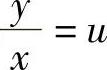 ,则y=xu,两端对x求导数,得
,则y=xu,两端对x求导数,得
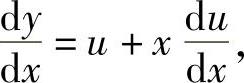
又因为
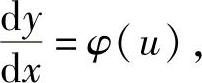
于是
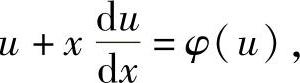
从而有
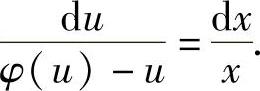
因此,方程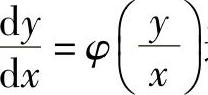 通过变量代换
通过变量代换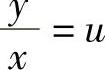 可化为可分离变量的方程.两边分别积分,得
可化为可分离变量的方程.两边分别积分,得
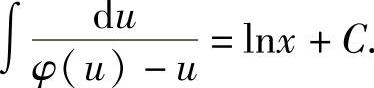
求出积分后,再用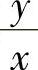 代替u,便得方程
代替u,便得方程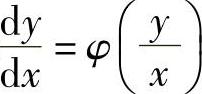 的通解.
的通解.
例6 求微分方程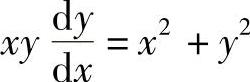 满足y(e)=2e的特解.
满足y(e)=2e的特解.
解 微分方程可化为
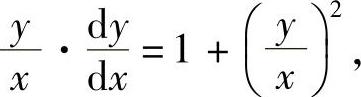
令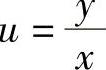 ,则
,则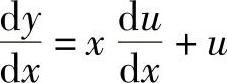 ,代入上式,得
,代入上式,得
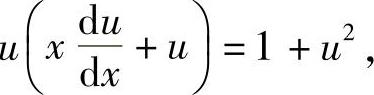
即
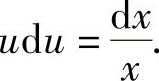
两边积分,得
u2=2lnx+C,所以原方程的通解为
y2=2x2lnx+Cx2,代入初始条件,解得C=2,故所求特解为
y2=2x2lnx+2x2.
例7 求微分方程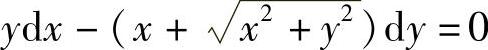 的通解.
的通解.
解 将方程改写为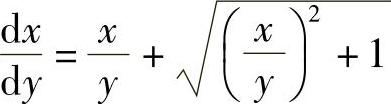 ,故原方程为齐次方程.作变量代换,令
,故原方程为齐次方程.作变量代换,令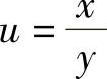 ,则x=uy,两端求导,得
,则x=uy,两端求导,得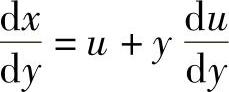 ,将上式代入方程,化简可得
,将上式代入方程,化简可得
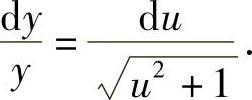 (www.chuimin.cn)
(www.chuimin.cn)
两端分别积分,得
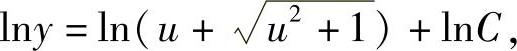
或
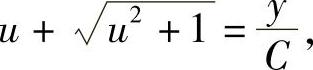
从而得
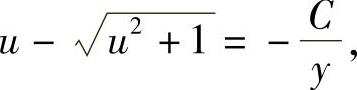
将
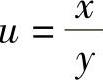
代入并整理,得原方程通解
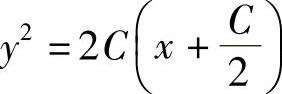
.
例8 探照灯的聚光镜的镜面是一个旋转曲面,它的形状是由Oxy坐标系上的曲线L绕x轴旋转而成的.按聚光镜性能的要求,其旋转轴(x轴)上一点O处发出的一切光线,经它反射后都与旋转轴平行.求曲线L的方程.
解 将光源所在的O点取作坐标原点(见图6-3),且曲线L位于y≥0范围内.
设点M(x,y)为L上的任意一点,点O发出的某条光线经点M反射后是一条与x轴平行的直线MS.又设过点M的切线AT与x轴的夹角为α.根据题意∠SMT=α.另一方面,∠OMA是入射角的余角,∠SMT是反射角的余角,于是由光学中的反射定律有∠OMA=∠SMT=α.从而AO=OM,但AO=AP-OP= ,而
,而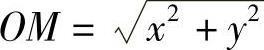 ,于是得微分方程
,于是得微分方程
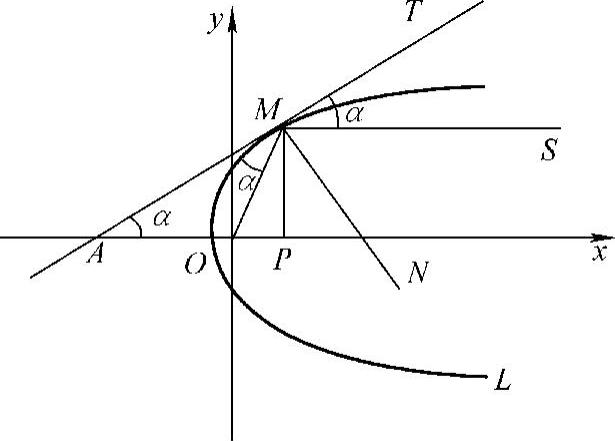
图6-3
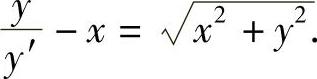

这就是齐次方程.令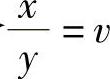 ,则x=yv,
,则x=yv,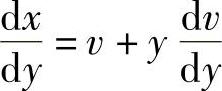 代入上式,得
代入上式,得
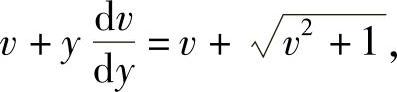
即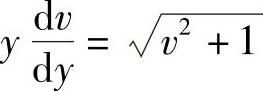 ,分离变量,得
,分离变量,得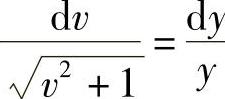 .
.
积分,得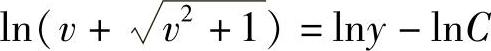 ,或
,或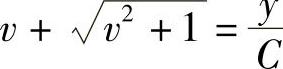 .
.
由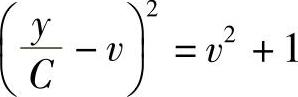 ,得
,得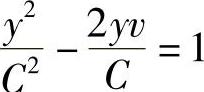 ,
,
以yv=x代入上式,得
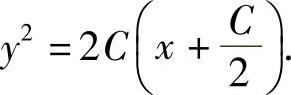
曲线L是以x轴为轴、焦点在原点的抛物线.三、一阶线性微分方程
形如

的微分方程,称为一阶线性微分方程.其中,P(x)和Q(x)都是x的已知连续函数.
特别地,若Q(x)≡0,方程(6-12)变为

式(6-13)称为一阶线性齐次方程.
当Q(x)不恒为零时,方程(6-12)称为一阶线性非齐次方程.
1.一阶线性齐次微分方程的通解
方程(6-13)是可分离变量的方程,当y≠0时可化为
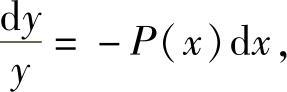
两边积分,得
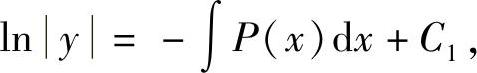
故一阶线性齐次方程的通解为
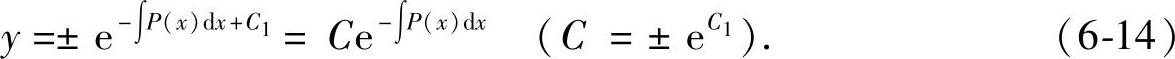
2.一阶线性非齐次微分方程的通解
为求得一阶线性微分方程式(6-12)的通解,将式(6-14)中的任意常数换成未知函数C(x),即设
y=C(x)e-∫P(x)dx (6-15)
是非齐次方程式(6-12)的形式的解,将式(6-15)以及它的导数y′=C′(x)e-∫P(x)dx-C(x)·P(x)e-∫P(x)dx代入方程式(6-12)中,得
C′(x)e-∫P(x)dx-C(x)·P(x)e-∫P(x)dx+C(x)P(x)e-∫P(x)dx=Q(x).
即
C′(x)e-∫P(x)dx=Q(x),或C′(x)=Q(x)e∫P(x)dx.
两端积分,得C(x)=∫Q(x)e∫P(x)dxdx+C1.
所以线性非齐次微分方程式(6-12)的通解为
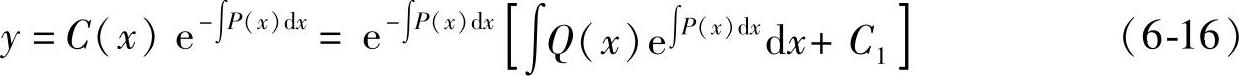
这种求非齐次微分方程通解的方法,叫做常数变易法.式(6-16)为一阶线性非齐次微分方程的求解公式.
例9 求方程xy′+y=ex的通解.
解 对应的齐次方程为
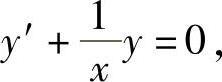
分离变量,得
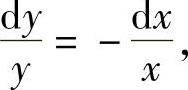
两边积分,得
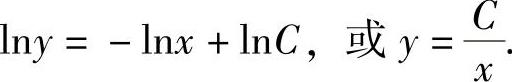
令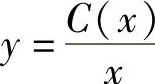 是原方程的解,代入到非齐次方程,得C′(x)=ex,故C(x)=ex+C,
是原方程的解,代入到非齐次方程,得C′(x)=ex,故C(x)=ex+C,
故原方程的通解为
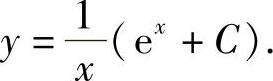
例10 解方程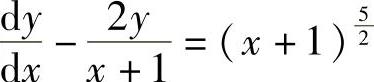 .
.
解 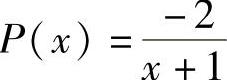 ,
,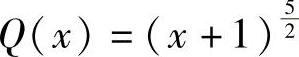 ,
,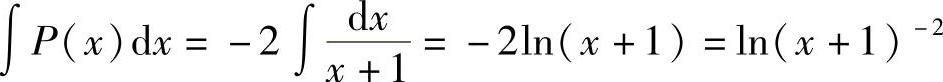 ,
,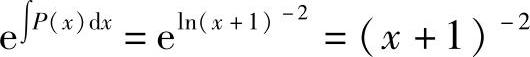 ,e∫P(x)dx=(x+l)2.
,e∫P(x)dx=(x+l)2.
方程的通解为
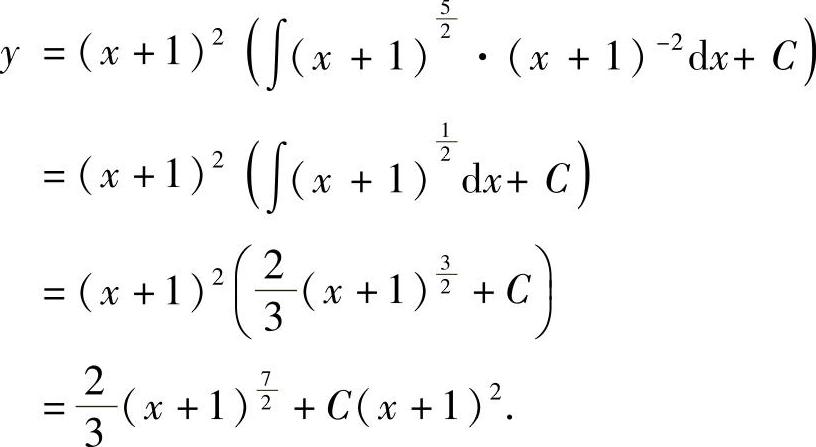
例11 设y=ex是微分方程xy′+u(x)y=x的一个解,求此微分方程满足条件y(ln2)=0的特解.
解 将y=ex代入方程xy′+u(x)y=x,得
u(x)=xe-x-x.
所以原微分方程变为
xy′+(xe-x-x)y=x,即
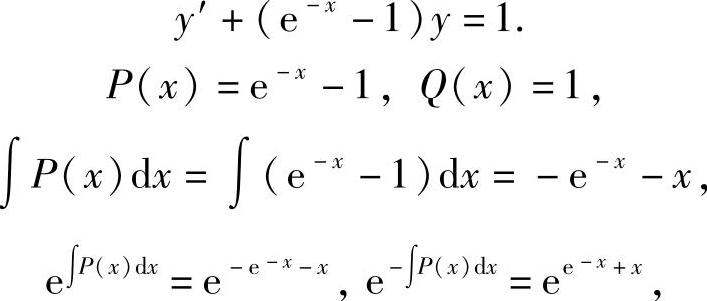
方程的通解
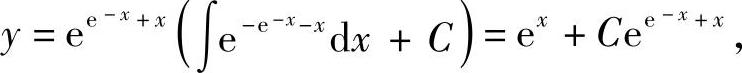
代入初始条件,解得C=-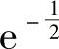 ,故所求特解为
,故所求特解为
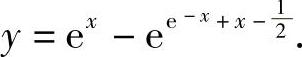
例12 设f(x)为连续函数,且满足
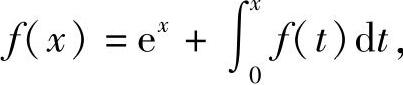 ,求f(x).
,求f(x).
解 方程两边对x求导,得
f′(x)=ex+f(x),即
f′(x)-f(x)=ex.
若记y=f(x),则上式变为
y′-y=ex,这是一阶线性非齐次微分方程,P(x)=-1,Q(x)=ex,由求解公式可得
f(x)=(x+C)ex.
由于在原方程中,有f(0)=1,代入上式,得C=1,于是有
f(x)=(x+1)ex.
例13 某商品在t时刻的售价为P,社会对该商品的需求量和供给量分别是关于P的函数Q(P)和S(P),则在t时刻的价格P(t)对于时间t的变化率可以认为与该商品在同一时刻的超额需求量Q(t)-P(t)成正比(设比例系数为k),即有关系式
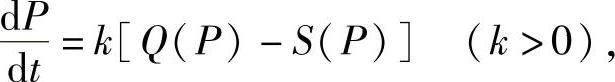
若Q(P)=c-dP,S(P)=-a+bP,这里a,b,c,d都是已知正的常数,且初始价格为P(0),试求价格P(t)的表达式.
解 将Q(P)=c-dP,S(P)=-a+bP代入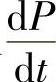 =k[Q(P)-S(P)]中,并整理,得
=k[Q(P)-S(P)]中,并整理,得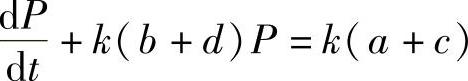 ,
,
若记m=k(a+c),n=k(b+d),则上式变为
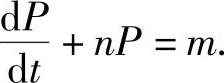
容易求得该方程的通解为
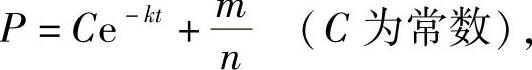
由初始价格P(0)=P0,则得价格P(t)的表达式为
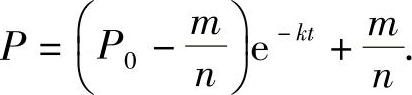
例14 假设某公司的净资产因资产本身产生了利息而以5%的年利率增长,同时,该公司还必须以每年200百万元的数额连续地支付职员工资.
1)求出描述公司净资产w(以百万元为单位)的微分方程;
2)解上述微分方程,这里假设初始净资产为w0(百万元).
解 1)现在用分析法来解此问题.为给净资产建立一个微分方程,将使用下面这一事实,即
净资产增长的速度=利息盈取速度-工资支付率.
以每年百万元为单位,利息盈取的速率为0.05w,而工资的支付率为每年200万元,于是我们有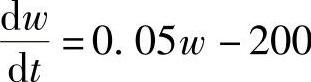 .其中,t以年为单位.
.其中,t以年为单位.
2)分离变量,有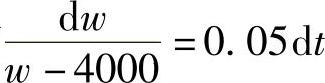 ,
,
积分得ln|w-4000|=0.05t+C,
于是w-4000=Ae0.05t,A=±eC.
当t=0时w=w0,有A=w0-4000,代入解中,得
w=4000+(w0-4000)e0.05t.四、可化为一阶线性方程的方程——伯努利(Bernoulli)方程
形如
y′+P(x)y=Q(x)yα(α为常数,且α≠0,1)的微分方程称伯努利方程.
将方程两端除以yα,得到
y-αy′+P(x)y1-α=Q(x).
令y1-α=z,有
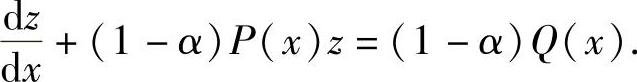
这是一个线性方程,可以求解.求出z之后,再用y带回,即得伯努利方程的解.
例15 求解微分方程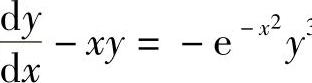 .
.
解 这是一个伯努利方程,令z=y-2,则有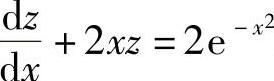 .
.
这是一阶线性方程,解之得z=e-x2(2x+C),
将z换成y-2,即得原方程的通解为y2=ex2(2x+C)-1.
有关高等数学(上、下册)的文章

知识要点1.微分方程的基本概念:微分方程的定义、阶、通解、特解.2.可分离变量的微分方程:求解可分离变量微分方程的步骤:(1)分离变量;(2)两端分别积分,可得原方程的通解.如果问题为求特解,只需将初始条件代入求得的通解,确定常数C的值即可.3.一阶线性非齐次微分方程:形式:y′+P(x)y=Q(x).求解方法有以下两种:(1)常数变易法:第一步,先求对应的齐次微分方程y′+P(x)y=0的通解......
2023-10-26

一、建立微分方程的数学模型解:设曲线方程为y=f(x),且曲线上任意一点的坐标为(x,y).根据题意以及导数的几何意义可得两边同时求不定积分得y=∫xdx,这就是所求的曲线方程.引例2求方程y"=cosx的通解.解:一次积分得:二次积分即得到方程的通解:以上我们仅以物理学、几何学引出关于变量之间微分方程的关系,其实在化学、生物学、自动控制、电子技术等学科中都提出了许多有关微分方程的问题,从而要......
2023-11-20

一般地,形如的一阶微分方程称为可分离变量的一阶微分方程.当g(y)≠0时,方程(7.2.1)可写为这样一来,变量y与x便被分离在等号的两端了.设f(x)与g(x)都连续,求解方程(7.2.1),就是要寻找函数y=y(x),将它代入方程(7.2.1)后,能使此方程成为恒等式.从而,当g(y)≠0时,就有在解微分方程时,为了突出任意常数C,常把中所含的任意常数C明确写出来.根据不定积分的第一换元法,得......
2023-10-19

【主要内容】1.一阶线性微分方程形如(其中P(x),Q(x)是已知函数)的微分方程,称为一阶线性微分方程,它的通解为(其中的不定积分都取一个原函数).2.伯努利方程形如(n≠0,1,P(x),Q(x)都是已知函数)的微分方程,称为伯努利方程.令z=y1-n,伯努利方程转换成一阶线性微分方程由式(1)的通解即可得到伯努利方程的通解.【典型例题】例4.2.1求微分方程的通解.精解 所给微分方程是一阶线......
2023-10-27

形如y′+p(x)y=q(x),其中,p,q与y,y′无关,但可以与x有关.它对y与y′而言是一次的,故称之为一阶线性微分方程.当q(x)=0时称为齐次线性微分方程;当q(x)≠0时称为非齐次线性微分方程.一、齐次线性微分方程的解法齐次线性微分方程的形式为:y′+p(x)y=0.此方程是可分离变量的微分方程,分离变量后,得:两边积分得:ln|y|=-∫p(x)dx,这就是齐次线性微分方程的一般解.......
2023-11-20

下面结合问卷和上节中我们对相关问题的设计、概念化和命题化,探讨因变量和自变量及其测量的问题。根据以上问题形成的变量虽然在大多数情况下是被用作因变量的,但在验证假设3的时候也会被用作自变量来对因变量集2进行考察。......
2023-12-02

定义1.3 称随机变量X1,…定义1.4 对于随机变量序列{Xk;k≥1},如果对每个n和所有的x1,…,xn,都存在某一独立于n的正常数M,使得(1.5)式和(1.6)式同时成立,则称{Xk;k≥1}是广义负相依序列。定义1.5 两个非负随机变量X1和X2是拟渐近独立的,如果如果X1和X2同分布,那么就说它们是渐近独立。如果随机变量序列{Xk,k≥1}中的任意两个随机变量都是QAI的,则称{Xk;k≥1}是两两AQI序列。......
2023-07-06
相关推荐