由此可以设想，可见光的频率从红端的384MMHz开始，在复频谱上按逆时针方向逐渐增加到紫端的768MMHz时，那些中间频率的相位从初始0相位逐渐增加到2π。在复频谱极坐标上，0、2π、4π等都是0相位，在可见光所有频率的相位仅仅分布在一个2π条件下，频率因子n就不能是正整数。可见光频率、波长与相位对应关系见书后附表。频率v与相位θ不仅成正比关系，而且呈环状均匀分布。......
2023-11-18
光矢量变换色矢量复频谱解析
【摘要】：在两级积分变换里，设定一个时间T，于是原本在时域t里光的动态频率v映射在复频谱上变成了复频域静态θ的相位。式Z=reiθ就是光色变换复频谱数学模型的表达式。拉普拉斯变换只是复数平面，Z变换则将复数平面进一步变换为周期循环的相平面。
光是电磁波，电磁波的波函数一般用如下形式表达：f=（x，y，z，t）。相对于光速而言，人在空间的位置可以看作静止的，所以可以把光的波动仅仅看作时间函数，用f （t）表示。应用现代通信科学“信号与系统”理论，光刺激视细胞后产生神经脉冲，不妨把神经脉冲看作Delta信号δ（t）的脉冲序列，即δ（t–nT）。式中n是从零到无穷大的自然数列；T是脉冲间隔时间。进入人眼的光是时域连续信号f （t），经过神经脉冲信号δ（t–nT）的处理，则变成了时域离散信号[9]，即：
显然，fs（nT）是一个时间间隔为T的经n次抽样离散的时域函数信号。这种信号只有在时间t等于T的整数倍时，信号fs（nT）才有值，当t ≠ nT时，fs（nT）=0。
在（4-2）式里T是时间常量，反映了在nT时间内进入一个锥体细胞的光子概率，与振幅相关。由此，（4-2）式的积分又可以写成如下求和式：
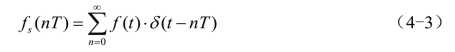
为了把时域信号变为复频域信号，需要对（4-3）式进行拉普拉斯变换，即将fs（nT）变换为Fs（s）：
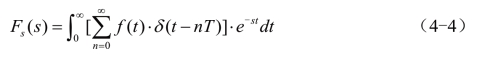
将（4-4）式的积分与求和前后次序对调一下，先积分再求和，得到：
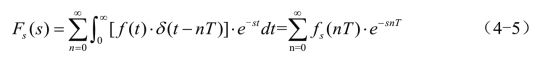
现在引入一个新的变量Z，进行Z变换，使Z平面与S平面成映射关系，即：
这样一来，（4-5）式中的复指数函数就变成了Z的复变函数，即：
那么，原来的拉普拉斯变换的复频域Fs（s），就变成了复变函数Z的负n次幂的求和式，即：
这是一个复变量Z-1的n次幂级数之和。如果|Z|>0，则级数收敛。(www.chuimin.cn)
在拉普拉斯变换里，复平面：S=σ+iω，是个复数；在Z变换里，Z平面：Z=reiθ，也是个复数。把两个复数平面联系起来，即：
（4-8）式中的fs（nT）项与视神经脉冲序列相关，实际上与光的振幅相关。（4-9）式中的eσT项，其中指数σ是个实数，如果σ<0，则eσT项递减。假设让eσT项与fs（nT）项相乘，即fs（nT）·eσT，则数列收敛。现在把Z变换与视神经脉冲序列联系起来fs（nT）·eσT 项相当于振幅r，于是
到此，（4-10）[10]式已不仅仅是一个积分变换式，在（4-10）式里r对应了光的振幅，而θ已不仅仅是相位（弧度），θ=ωt，又因为ω=2πv，v是光的频率。在Z平面上，相位θ对应的是光的频率。在两级积分变换里，设定一个时间T，于是原本在时域t里光的动态频率v映射在复频谱上变成了复频域静态θ的相位。也就是说，在一定时刻T，可见光的不同频率映射在Z的极坐标复平面上均匀地分布在不同相位（弧度）上。光在进入眼睛以前是电磁波，一旦进入眼睛，经过T时信号处理，被人感知，光就变成色了。在Z平面上，光的振幅与矢径r相关，光的频率与相位θ相关。不同的频率，对应不同的相位，显示不同的颜色。这就是在Z平面上光与色有对应的物理意义。（4-10）式Z=reiθ就是光色变换复频谱数学模型的表达式。
有朋友会问，为什么要进行这些积分变换？光无论是波动性还是光子的动量都具有矢量性。我们设定颜色也具有矢量性。那么只有在复数域里才能找到光与色的映射关系。另外，积分变换的妙处在于通过它就可以把动态的时域变量变换成静态的频域变量。而又可以把频率变换成相位，将频率与色相对应，这样一来，就给颜色赋予了与光对应的物理性能。
那么，既然拉普拉斯变换的S域eσ+iω已经是复数域了，如图4-2所示，为什么还要进行Z变换？在图4-2拉普拉斯变换S域里，σ是实轴。而与频率相关的iω在虚轴上。我们知道，可见光的频率在电磁波大家族的频域里只占很窄的一小部分，而且可见光红端以外的频率继续向更低的方向延伸；而蓝端以外的频率也继续向更高的方向延伸。红蓝两端延伸的方向相反，它们两端在S域复平面上不可能重叠。
与频率相关的是色相，大量人工视觉实验表明，可见光产生的颜色按频率排列，红端颜色与蓝端颜色在色相上却是接近的。由它们俩合成的紫红色从蓝到紫红再到红，在色相的变化上也是连续性的。可是在拉普拉斯S域的虚轴上无法实现这种周期性的重叠与连续。考虑到在Z变换里将圆频率ω变换成相位θ（0～2π），呈现出的周期变化，恰好可以满足色相变化的要求，Z变换Z平面如图4-3所示。
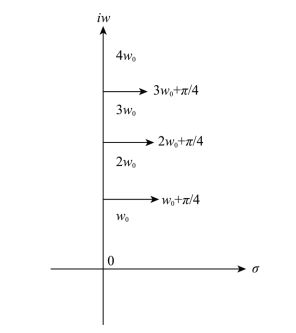
图4-2 拉普拉斯变换S平面（S=σ+iω）
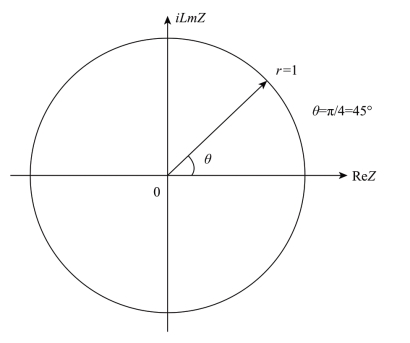
图4-3 Z变换Z平面（Z=reiθ）
在Z平面里，若以某一个频率为基频v0，假设这个基频位于零相位，那么与这个基频所有正整数n的倍频的频率转过n个2π后都与基频处在同一个零相位上。而这个倍频内其他频率则会均匀地分布在Z平面0～2π相位上。可见光红端的频率为384MMHz，紫端的频率为768MMHz，恰好是一个倍频。这样红紫两端的相位都重叠在零相位上。由频率映射的色相在Z平面上形成一个封闭的、连续的色相环。
拉普拉斯变换只是复数平面，Z变换则将复数平面进一步变换为周期循环的相平面。虽然二者表征的都是矢量，但是光从Z变换复平面上的相矢量（phasor）映射到复频谱变成色矢量，不仅能够将频率的变化与色相的变化一一对应，更能表达色相变化的规律，从而证明当年牛顿假想的颜色环是有科学依据的。
有关光矢量变换色矢量复频谱色度理论解析的文章
- 详细阅读
-
光矢量变换色矢量复频谱色度理论解析-平衡效率详细阅读
当色矢量r1与r2合成rp时产生h1和h2两个平衡矢量如图8-1所示。可以看到平衡色矢量模的大小既与r1与r2模的大小有关，也与φ及α与β大小有关。假若r2=r1，n=1，α=，这时也就是说只有在r2=r1与α=β=的条件下，才有最大的平衡效率ηba。（8-3）式表明若r1与r2为一对互补色矢量，并且φ=180°时，ηba=1，两色矢量完全平衡，转化为中性色。......
2023-11-18
-
光矢量变换色矢量复频谱色度理论解析结果详细阅读
复频谱色度计算不需要把可见光分成红、绿、蓝三个原色，它只需要一台分光光度计把每一个频率相对功率分布或反（透）射率以矢端函数曲线的形式记录下来。可见光全频域由无限多个微色矢量端点连续绘出矢端函数曲线，形成一个色矢量系统，有了矢端函数曲线就可以计算出复频谱颜色特征数值。一般说矢端函数曲线在复频谱上包围的面积越大，它被平衡的色矢量强度也越大，白色越多，亮度也越高。......
2023-11-18
-
光矢量变换色矢量复频谱色度图解析详细阅读
图5-4是用玫瑰红、大红、中黄、绿、天蓝、深蓝6种油墨调配出来的复频谱色相图，在二维平面上把全色相域分成36份，每相邻两个色块，其色相差大约在10°。图5-4六种颜色油墨调配的复频谱色相图我们说可见光的频率范围在384MMHz到768MMHz之间，这并不是说频率低于384MMHz和频率高于768MMHz的光被眼睛拒之门外。这正是复频谱分析中Z变换与拉普拉斯变换的区别所在。但它们映射在复频谱上的相位转过360°一周后，两端却又重合了。......
2023-11-18
-
光矢量变换色矢量复频谱色度理论解析-同色异谱详细阅读
同色异谱这一命题表明色与谱二者之间确实存在着微妙的关系。“同色”指两个物体的颜色完全相同；“异谱”则是两个相同颜色的辐亮度光谱结构却不同。但是电视上的绿色是由荧光屏上红、绿、蓝三基色加和产生的，这里三基色的光谱结构与树叶中叶绿素分子的光谱结构肯定不同，也就是说这二者是同色却是异谱。人们只需做到是同色，不必刻意追求同谱。解释同色异谱的奥秘就在于复频谱里的色矢量。......
2023-11-18
-
近代颜色科学的兴起-光矢量变换色矢量复频谱色详细阅读
十七世纪英国天才科学家牛顿总结亲历的实验，为近代颜色科学做出了开创性的贡献。图3-1牛顿颜色环十九世纪初，英国年轻科学家杨以杨氏光干涉实验力挺光的波动说，反对牛顿的微粒说。说到颜色科学家，不能不提到格拉斯曼，他在1854年提出颜色变化的三条定律。在色彩学上称“同色异谱”。科学技术要求对颜色变化的规律给出定量的描述。......
2023-11-18
-
光矢量变换与复频谱色度理论解析详细阅读
不同色光相加不是在能量层级上相加，在复频谱上是它们的色矢量相加。人眼虽然看不见色矢量，我们可以把一个准单色光的能量、微弧度及色矢量映射在复频谱图上。虽然微弧度Δθ很窄，可是它里面众多的色矢量分别处在以r为中心均等对称的相位上，这些色矢量在自发地合成中心色矢量r时，在色矢量r的垂直方向又合成出两个大小相等但是方向相反的分色矢量。很显然，这些分色矢量会自发地互相平衡。......
2023-11-18
-
常用印刷油墨复频谱色度图及光矢量变换色矢量复详细阅读
下面列出了12种油墨的复频谱颜色特征数值，如表9-1所示，绘制出该12种油墨的复频谱色度图，如图9-1到图9-12所示。以图9-2桃红油墨为例，复频谱色相值为25.3921°，它的矢端函数曲线包围的面积大部分在红色区域。复频谱色相与光的频率、波长相对应，而在CIELab色度系统中，其色相值没有上述对应关系。更为重要的是，如图9-7所示，中黄油墨的复频谱饱和度为39.5378，而CIE-Lab的饱和度高达109.8755。......
2023-11-18
相关推荐