首页理论教育指数函数与对数函数使用方法

指数函数与对数函数使用方法

2023-10-30 理论教育版权反馈

【摘要】：指数函数w = ez在全平面上解析,且(ez)′ = ez 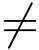0,因而在全平面上都是保角的.设z =x+iy,w =ρeiφ,则由ρeiφ =ex·eiy得由此可知,在w = ez映射下,z平面上的直线x = x0(实常数)映射成w平面上的圆周ρ = ex0,直线y = y0(实常数)映射成射线argw = φ = y0,带形域0 ＜y ＜y0(≤2π)映射成角形域0 ＜arg w ＜y0.特别地,

指数函数w = ez在全平面上解析,且(ez)′ = ez pagenumber_ebook=193,pagenumber_book=184 0,因而在全平面上都是保角的.

设z =x+iy,w =ρeiφ,则由ρeiφ =ex·eiy得

由此可知,在w = ez映射下,z平面上的直线x = x0(实常数)映射成w平面上的圆周ρ = ex0,直线y = y0(实常数)映射成射线argw = φ = y0,带形域0 ＜y ＜y0(≤2π)映射成角形域0 ＜arg w ＜y0.特别地,带形域0 ＜y ＜2π映射成沿正实轴剪开的w平面：0 ＜arg w ＜2π(图6.19),且它们之间的点是一一对应的.

pagenumber_ebook=194,pagenumber_book=185

对数函数w = ln z是指数函数z = ew的反函数,它在区域D : -π ＜argz ＜π内解析,在D内

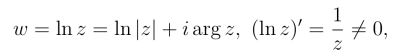
pagenumber_ebook=194,pagenumber_book=185

因此它在D内是保角映射.

对于角形区域D1 : α ＜argz ＜β(-π ≤α ＜β ≤π),在D1中z 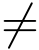pagenumber_ebook=194,pagenumber_book=185 0,设w =u+iv,由于

u=Rew =ln|z|,v =arg z =Imw,

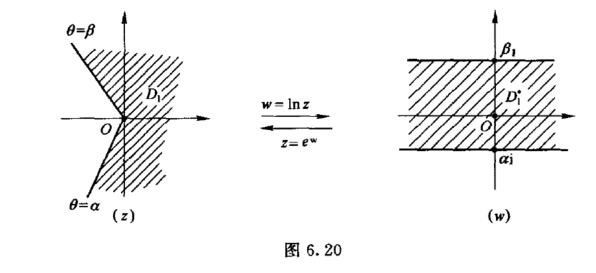
因此区域D1映射为带形区域 pagenumber_ebook=195,pagenumber_book=186 (图6.20).

pagenumber_ebook=195,pagenumber_book=186

其逆映射z =ew将带形区域D*1映射为角形区域D1.

对于角形区域为0 ＜Argz ＜β(π ＜β ≤2π) 的情形.可用w1 = e-lπz使该区域内各点的辐角减少π变为

由于映射w1 = -z,w2 = lnw1,w = w2 +πi依次把区域0 ＜Argz ＜β变为-π ＜Argw1 ＜β-π,再变为-π ＜Imw2 ＜β-π,最后变为0 ＜Imw ＜β,其复合映射为w =ln(-z)+πi,逆映射-z =ew+πi =-ew,因此

综上,对于π ＜β ≤2π.指数映射w = ez仍然将带形区域0 ＜Imz ＜β映射为角形区域0 ＜Argw ＜β; 其逆映射z = ln(-w)+πi,也是保角映射,且是一一对应的.(www.chuimin.cn)

例3 试讨论对数映射w =ln z分别将下列区域映射为什么区域.

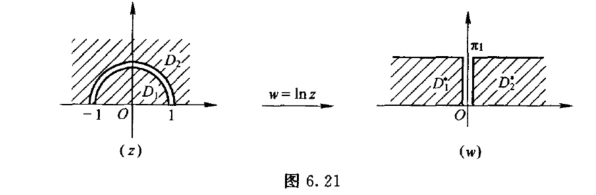
(1)D1 :|z|＜1,0 ＜arg z ＜π

(2)D2 :|z|＞1,0 ＜arg z ＜π

解由于w =ln|z|+i arg z,

u=ln|z|,v =arg z

当z ∈D1时,有-∞＜u ＜0,0 ＜v ＜π,

当z ∈D2时,有0 ＜u ＜∞,0 ＜v ＜π.

这表明,映射w =ln z分别将区域D1和D2 映射为D′1和D′2(图6.21).

pagenumber_ebook=196,pagenumber_book=187

pagenumber_ebook=196,pagenumber_book=187

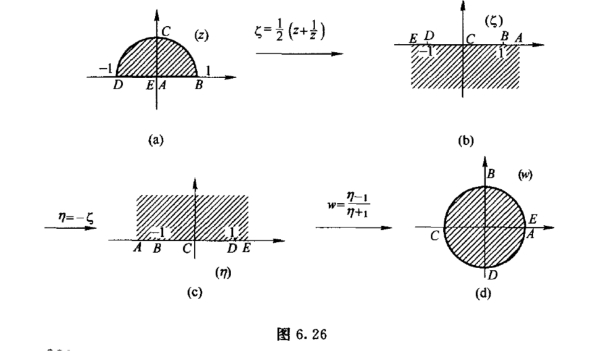
例4 求一函数,它把新月形域：保角地映射成上半平面.

解首先把新月形域映射成带形域,作分式线性映射w1 =则z 平面上的点0,i,-i分别映射成w1平面上0,∞, 所给区域映射成竖带形域,带宽为

其次作映射w2 = =iw1,将竖带形域逆时针旋转映射成横带形域.

再作映射w3 =2πw2,将带宽放大到π.

最后通过指数函数w =ew3将横带形域映射成上半平面(图6.23).

因此,将上述函数复合,得到所求的函数为

pagenumber_ebook=197,pagenumber_book=188