首页理论教育函数微分的概念与定义

函数微分的概念与定义

2025-09-30 理论教育版权反馈

【摘要】：【主要内容】1.函数微分的定义设函数y=f（x）在点x0的某个邻域内有定义.如果y在点x0处的增量Δy=f（x0+Δx）-f（x0）（其中，Δx是自变量x在点x0处的增量）可表示为Δy=AΔx+o（Δx）（其中，A与Δx无关，o（Δx）表示Δx→0时比Δx高阶的无穷小），则称y=f（x）在点x0处可微，称Δy的线性主部AΔx为y=f（x）在点x0处的微分，记为dy|x=x0（注意：函数y=f（x

【主要内容】

1.函数微分的定义

设函数y=f（x）在点x₀的某个邻域内有定义.如果y在点x₀处的增量

Δy=f（x₀+Δx）-f（x₀）（其中，Δx是自变量x在点x₀处的增量）可表示为

Δy=AΔx+o（Δx）（其中，A与Δx无关，o（Δx）表示Δx→0时比Δx高阶的无穷小），则称y=f（x）在点x₀处可微，称Δy的线性主部AΔx为y=f（x）在点x₀处的微分，记为dy|_x=x₀（注意：函数y=f（x）在点x处的微分记为dy）.

如果函数f（x）在区间I的每个点处都可微，则称f（x）在I上可微.

2.函数微分的性质

（1）函数y=f（x）在点x处可微的充分必要条件是y=f（x）在点x处可导，此时，dy=f′（x）dx，其中dx=Δx（即自变量微分与自变量增量相等）.

（2）设函数y=f（u）可微，则不管u是自变量还是中间变量，都有

dy=f′（u）du.（微分形式不变性）

3.函数微分的应用

计算函数f（x）对函数u（x）的导数.

设f（x），u（x）都是可微函数，且u′（x）≠0，则

【典型例题】

例1.12.1 （单项选择题）设函数y=f（x）可导，且曲线y=f（x）在点（x₀，y₀）（其中，y₀=f（x₀））处的切线与直线y=2-x垂直，则当Δx→0时，dy_x=x₀是（）.

A.与Δx同阶但非等价的无穷小 B.与Δx等价的无穷小(https://www.chuimin.cn)

C.比Δx高阶的无穷小 D.比Δx低阶的无穷小

精解由题设算出f′（x₀）即可判断应选哪个选项.

由曲线y=f（x）在点（x₀，y₀）处的切线与直线y=2-x垂直可知

所以，dy|_x=x₀=f′（x₀）Δx=Δx，即Δx→0时，dy|_x=x₀是与Δx等价的无穷小.

因此本题选B.

例1.12.2 设函数f（x）可导，且对函数y=f（x²），当自变量x在点x=-1处的增量Δx=-0.1时，相应的函数增量Δy的线性主部为0.1，求f′（1）.

精解设Δy为可导函数φ（x）在点x₀处的增量，则它的线性主部为φ′（x₀）Δx.

于是根据题设有

所以，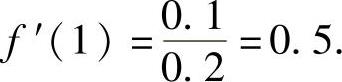

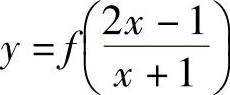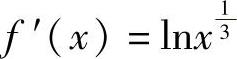例1.12.3 设函数，且，求dy.

精解

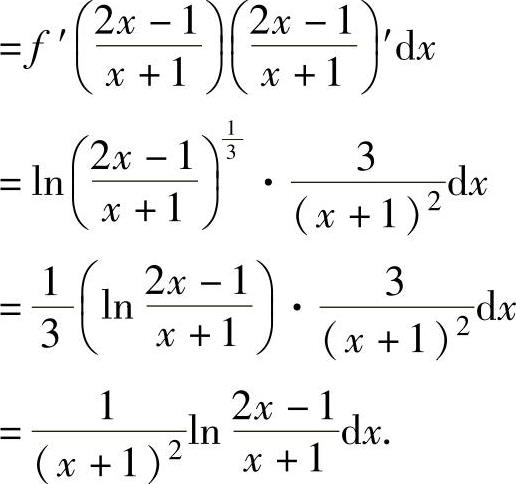
例1.12.4 设函数y=y（x）是由方程x²y-e^2y=sin（xy）确定，求dy.精解利用微分形式不变性，对所给方程两边求微分得d（x²y）-de^2y=dsin（xy），

即2xydx+x²dy-2e^2ydy=cos（xy）（ydx+xdy）.

合并同类项得[x²-2e^2y-xcos（xy）]dy=[ycos（xy）-2xy]dx，所以，