根据双脚落地约束的状况,系统自动把运动划分为腾空阶段和足触地阶段。2)运动路径提取与编辑运动路径path是一种特殊的运动轨迹。本文采用3次NURBS曲线来拟合根节点轨迹曲线。在腾空阶段,由于不受外力作用,如果运动速度与原始运动差别较大,将会导致物理失真。根据式(5-6)进行路径变换,求出结果运动的根轨迹。4)试验结果图5-8和图5-9给出了我们的运动轨迹编辑方法的部分试验结果。......
2023-10-17
运动编辑就是通过修改运动捕获数据,使之适合用户设定的新角色、新场景或新约束等,同时保留原有的自然、逼真的运动特征。基于运动曲线编辑的方法,需要调整运动的每个自由度曲线,过程极为繁琐;基于IK的关键帧编辑算法,存在着插值曲线跳跃性过大,样条控制点间距难以设定的缺点。为此,我们研究利用层次化样条曲线来自动确定样条控制点的间距。给定原始运动序列,用户利用IK算法调整原始运动的若干关键帧姿态,系统自动利用层次化样条曲线拟合运动的偏移图,生成光滑的运动曲线,得到结果运动。
整个算法包括解析逆向运动学、多层次运动曲线拟合和在线运动编辑三大步骤。
1)解析逆向运动学算法
逆向运动学算法是运动编辑中的核心算法。具有n个自由度的运动链,其运动学方程式可以写成:
![]()
其中q1,q2,…,qn是n个关节变量,T是变换矩阵,G是目标变换矩阵。逆向运动学所要求解的问题是已知目标矩阵G,求解关节变量q1,q2,…,qn。
Tonali提出一种解析IK算法[102],用于求解逆向运动学问题,它比数值IK法更加快速和鲁棒。该算法用于求解7个自由度的四肢链,不失一般性,我们以右腿为例进行说明。
首先计算右腿运动链上各关节的角度,使右踝的目标配置得以满足。假定右臀、右膝、右踝的全局位置分别为PH、PK和PA,右踝的约束位置为PT。设右大腿和右小腿的长度分别是l1和l2,它们在旋转平面上的投影分别为l1′和l2′,则目标右膝关节转角θ可由式(5-2)计算。
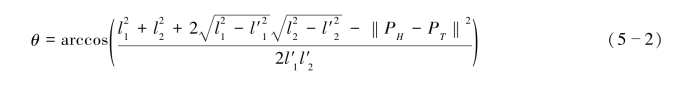
现在右踝位于新位置PA′,我们通过旋转右臀来使右踝位于目标位置,然后旋转右踝使其朝向满足要求。
因为腿有7个自由度而目标配置约束只有6个(3个旋转,3个平移),系统存在一个冗余的自由度。可以将右腿沿轴PH PA旋转,而不违反任何约束,这一多余的自由度称为“肘园”。我们的算法通过调整该自由度使得右踝的局部朝向尽量与其初始局部朝向相同。设ΔQ是应用在右踝关节上使右踝位于目标朝向的旋转,其四元数形式为(w,v),则我们将右腿绕轴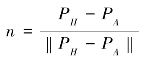 旋转的角度Φ如式(5-3)所示
旋转的角度Φ如式(5-3)所示

其中符号根据最大化ΔQ·QΦ选取,QΦ是右臀的朝向。
2)多层次运动曲线拟合
之所以选择多层次曲线拟合方法来进行运动偏移的叠加,是因为多层次曲线拟合能够在给定精度下确定所需要的B样条曲线控制顶点,避免当帧数过多时控制顶点过于密集;而且采用多层次运动曲线拟合技术可以避免曲线跳动太大(Overshooting)。下面介绍如何将多层次B样条拟合技术应用到运动曲线的拟合中。
定义Ω={t∈R|0≤t<n}为一个均匀分布的时间域。考虑一系列的散乱数据点P={(ti,yi)},ti∈Ω,这里ti可以认为是第i帧所处的时刻,yi是在ti时刻关节的转角值。定义均匀三次B样条逼近函数![]() ,其中0≤k≤3,0≤t≤1,Bk是基函数,bj是第j个控制顶点,-1≤j≤n+1。问题的关键在于如何求解控制顶点bj(-1≤j≤n+1),使f(t)最佳逼近于散乱数据点集P。
,其中0≤k≤3,0≤t≤1,Bk是基函数,bj是第j个控制顶点,-1≤j≤n+1。问题的关键在于如何求解控制顶点bj(-1≤j≤n+1),使f(t)最佳逼近于散乱数据点集P。
对于均匀三次B样条,它的每个控制顶点bj都受相邻的四个点的影响,我们将其这点邻域点定义为邻域点集Pj={(ti,xi)∈P|j-2≤ti≤j+2},可以使用伪逆法求解需要的控制顶点。(www.chuimin.cn)
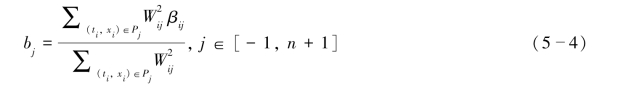
这样能够将局部误差![]() Wij=Bj+1-⎿ti」(ti-⎿ti」)表示均匀三次B样条函数。
Wij=Bj+1-⎿ti」(ti-⎿ti」)表示均匀三次B样条函数。
考虑时域上的层次式控制顶点S0,S1,…,Sh。假定S0中控制顶点的间距是事先给定的,然后依次往下,从S1到Sh控制顶点的个数依次减少一半。因此,假如Sk有m+3个控制顶点,则下一层Sk+1中控制顶点的个数为2m+3。
多层次B样条拟合方法首先求解最初始的控制顶点集S0,得到拟合函数f0,此时由于控制顶点个数少,因此对于散乱数据点集P中的点(ti,xi)会存在的误差Δ1xi=xi-f0(ti)。下一步是使用更多的控制顶点对每个点存在误差值进行拟合,得到函数f1。这样f0+f1得到了比f0更高的拟合精度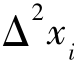 =xif0(ti)-f1(ti)。在第k层,我们的目标是寻找控制点集Sk,使逼近函数fk逼近于误差项Pk={(xi,
=xif0(ti)-f1(ti)。在第k层,我们的目标是寻找控制点集Sk,使逼近函数fk逼近于误差项Pk={(xi,![]() 其中
其中![]() 最终得到所需要的拟合函数f,它是前面k+1个函数的和,即
最终得到所需要的拟合函数f,它是前面k+1个函数的和,即![]()
3)运动变形和在线编辑
人体的运动通常表示为根节点的平移,各关节点相对于父关节点的偏移量和各关节点的转角。一个运动可以表达为m(t)=f(R(t),θ(t)),其中R(t)∈R3表示根节点的平移量,θ(t)∈R3×m表示各关节的旋转分量,m是关节的个数。同时一个运动也可以参数化为一系列的运动曲线。为了获得新的运动序列,可以对每条运动曲线单独进行变形,目标是寻找函数bi(t)使之满足θ′i(t)=ai(t)θi(t)+bi(t)和约束对(ti,θi)。这里的ai(t)是运动缩放因子,bi(t)是运动偏移因子。我们没有考虑运动的缩放,仅考虑了运动的偏移,所以ai(t)=0。可以使用上述多层次运动曲线拟合算法计算出bi(t)。
整个在线编辑过程为:首先用户指定运动的关键帧和约束对(tj,cj),之后使用反向运动学求解器对每个关键帧进行求解,在得到每个关键帧中每个关节的运动偏移量(tj,xj)后,使用多层次B样条曲线对这些偏移量进行拟合,最后将对相邻帧的转角加上计算出的分量bi(t)就可以得到需要的光滑运动序列。
4)试验结果
在图5-4中,我们将一个“走路并在中间回头”的运动编辑为一个“走路并在中间回头并挥手告别”的运动。在图5-5中我们编辑了一个后踢腿动作,使腿踢的高度增加,并保证中间序列的光滑过渡性。
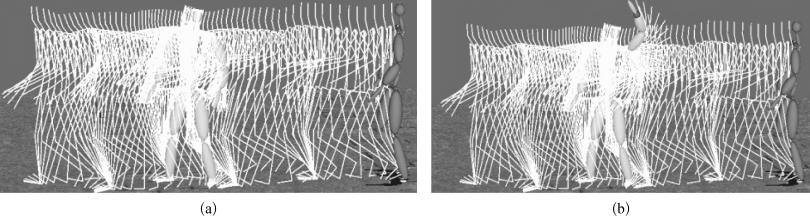
图5-4
(a)初始运动序列是一个“走路并在中间回头”的运动序列 (b)编辑后的运动序列,此时的运动在中间有一个挥手的动作,而且相邻的帧也相应地改变了,运动的过渡是光滑的

图5-5
(a)初始运动序列是一个“跳起来踢”的运动序列 (b)编辑后的运动序列,此时腿踢的高度变大,而且相邻的帧也相应地改变了,运动是光滑过渡的
有关虚拟现实理论基础与应用开发实践的文章

根据双脚落地约束的状况,系统自动把运动划分为腾空阶段和足触地阶段。2)运动路径提取与编辑运动路径path是一种特殊的运动轨迹。本文采用3次NURBS曲线来拟合根节点轨迹曲线。在腾空阶段,由于不受外力作用,如果运动速度与原始运动差别较大,将会导致物理失真。根据式(5-6)进行路径变换,求出结果运动的根轨迹。4)试验结果图5-8和图5-9给出了我们的运动轨迹编辑方法的部分试验结果。......
2023-10-17

我们研究基于时空配准的运动插值算法,解决人体运动的参数插值问题,包括时间配准、空间配准、帧插值和约束重建四个步骤。下面以两个运动M1、M2为例,介绍基于时空配准的运动插值算法。图5-13显示了采用贪心算法得到的配置曲线的效果图。严格来说,方位配准曲线与时间配准曲线完全不同,并非一条坐标系下的曲线,而是基于时间配准曲线的一系列数值。......
2023-10-17

图5-15结构表示意图3)过渡运动构建运动图的核心思想就是在不同运动之间寻找过渡点,在相似帧之间构造过渡运动,把初始的运动集组织成一个图结构。......
2023-10-17

直接照明是一个被老式渲染引擎所采用的主要光照方法。表4-1阴影产生方法需要考虑的最重要的问题是,由于这些方法会产生超越真实的图像,他们只能处理只有点光源的场景,而且场景中的物体都能做到完美地反射和漫反射。同时也应该注意到,在真实世界里,我们仍然能看到不被直接照亮的物体。直接照明的渲染器试图通过加入环境光来解决这样的问题。这样一来所有的物体都接收到一个最小的普遍直接照明值。......
2023-10-17

钢的淬透性曲线在合理选材、预测材料组织性能以及制定热处理工艺等方面都具有重要的实用价值。图3-2340Cr钢端淬曲线带根据端淬试验曲线,确定热处理工艺。首先,根据钢的碳含量从图3-14中查出半马氏体区的硬度值,再利用钢的淬透性曲线求得与该硬度值对应的端淬试样上至水冷端的距离,最后利用确定淬透性的线解图便可求出在某种淬火介质中应有的临界淬透直径。根据淬透性曲线确定钢的临界淬透直径。......
2023-06-24

图3-65 “绘图工具/格式”选项卡3.6.3 插入与编辑公式编撰学术论文时,经常需要在文档中插入各种形式的数学公式。自测习题一、单选题1.在Word 2010中不能直接被编辑的文件类型是_________。A.内存B.外存C.磁盘D.CD-ROM4.编辑Word文档时,中英文的切换键是_________。......
2023-11-26

辐射度的算法分为三个步骤[26]。两个patch之间的形式因子表示了一个patch出射的光有多少比例会被另一个patch接收。辐射度算法会非常的慢,而且如果不考虑额外的复杂度,辐射度算法很难计算镜面反射,改进的辐射度算法可以缓解这一问题。很多研究者都试图结合光线追踪和辐射度这两种方法,以期达到各自的优势。对于,我们收集来自caustics map中的光子信息。即使是photon map算法,对于普通硬件,暂时也只能用于静态渲染。......
2023-10-17

用样条曲线编辑命令可编辑样条曲线,或将样条曲线拟合为多段线。“闭合”是闭合开放的样条曲线或打开闭合的样条曲线。“清理”是从图形数据库中删除样条曲线的拟合数据。“切线”是编辑样条曲线的起点和端点切向。“公差”是使用新的公差值将样条曲线重新拟合至现有点。单击“修改Ⅱ”工具栏中的“编辑样条曲线”按钮,命令行提示如下。......
2023-10-21
相关推荐