信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致,必须存在一个各导弹共同关心的变量,这称为信息状态。此外,还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法,这称为一致性算法。因此,可将一致性理论应用于多导弹编队,基于一致性算法来设计导弹的编队控制算法。......
2023-08-02
本书用有向图Gn≜(vn,εn)作为n个导弹通信拓扑的模型,其中vn={1,2,…,n}为节点集,εn⊆vn×vn为边集。令矩阵An=[aij]∈Rn×n为图Gn的邻接矩阵,aij表示两个导弹i、j之间的连接权重,对于所有i=1,2,…,n和j=1,2,…,n,如果(j,i)∈εn,则aij>0(即导弹i能接收到导弹j的信息),否则aij=0,除非特殊说明,一般aii=0。矩阵Ln=[lij]∈Rn×n,为图Gn的拉普拉斯矩阵。其中,对于i,j=1,2,…,n,lii表示导弹i能接收到其他导弹信息的连接数,lii=![]() ;当i≠j时,lij=-aij。对于无向图来说,它的邻接矩阵中的元素aij=aji,拉普拉斯矩阵是实对称矩阵。
;当i≠j时,lij=-aij。对于无向图来说,它的邻接矩阵中的元素aij=aji,拉普拉斯矩阵是实对称矩阵。
以图6-1来举例说明有向图的定义。
在图6-1表示的有向图G4≜(v4,ε4)中,节点集v4={1,2,3,4},边集ε4={(1,2),(2,1),(2,4),(2,3),(3,2),(4,3),(4,1)},邻接矩阵A4=[aij]∈R4×4,为
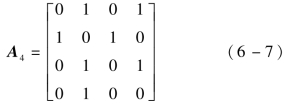

图6-1 某有向通信拓扑图
拉普拉斯矩阵为
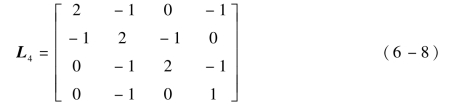
因为拉普拉斯矩阵的各行元素之和为0,因此0是L4的一个特征值,其对应的特征向量是元素均为1的4×1维的列向量。拉普拉斯矩阵L4的特征值D和特征向量V为

拉普拉斯矩阵具有以下性质:如果通信拓扑图中包含一簇有向生成树,那么其拉普拉斯矩阵有唯一的零特征值。
有关多飞行器协同制导与控制的文章

信息一致性保证了按一定网络拓扑交换信息的多导弹在那些对完成协同任务起关键作用的“信息”方面达成一致意见。为了达到信息一致,必须存在一个各导弹共同关心的变量,这称为信息状态。此外,还需要设计用于各导弹之间相互协商以使其信息状态达成一致的适当算法,这称为一致性算法。因此,可将一致性理论应用于多导弹编队,基于一致性算法来设计导弹的编队控制算法。......
2023-08-02

本节阐述如何确定满足攻击时间要求的附加指令uF。联立式、式,可以得到加速度指令,也就是基于线性模型得出的ITCG导引律,为由式可知,当导弹接近目标时,xgo趋于0,此时上述制导指令会趋于无穷大。表8-14枚导弹的初始参数图8-3给出了4枚导弹采用PNG和ITCG时的弹道对比。在采用PNG时,导弹1、导弹2、导弹3和导弹4的攻击时间分别为35.67 s、30.83 s、27.40 s和31.89 s,4枚导弹采用PNG时的攻击时间差较大,最大攻击时间差为8.27 s。......
2023-08-02

多飞行器协同飞行,当攻击目标时,如果能够从不同的方向同时命中目标,则能够大大提高对目标的攻击性能。要想实现此目的,需有协同末制导律作为技术支撑。进一步,在设计协同末制导律时,还需考虑各导弹的控制量受限、框架角受限等约束问题。对于通过信息传输实现协同攻击的多导弹,信息的传输模式、通信拓扑的设定和信息的利用规则是设计协同末制导律的关键问题。......
2023-08-02

在目标、防御弹1和防御弹2协同对攻击弹拦截的过程中,目标和防御弹1采用式所示的协同拦截制导律飞行,防御弹2则跟踪防御弹1的弹目距离,最终实现和防御弹1同时拦截攻击弹。因此,当防御弹1与防御弹2距离攻击弹很近时,令防御弹2转为采用式所示的可实现落角约束的弹道成型制导律。......
2023-08-02

而为了占领战争的优势地位,战争另一方往往发射机动导弹对无人战机进行袭击。如果攻击弹具有强大的威力,那么为了能够成功拦截并摧毁它,则目标可能需发射多枚防御弹进行协同拦截。此时,一方面,涉及防御弹与目标的协同问题;另一方面,涉及多枚防御弹对攻击弹进行协同拦截的问题。......
2023-08-02

需要说明的是,基于10.2节的模型,式中的综上,基于MPSP的三维协同制导律的实现流程如下:第1步,综合考虑弹群中各弹的初始位置及速度,为虚拟领弹设置合适的初始位置及速度。采用MPSP制导律则在原具有攻击时间约束的弹道基础上对其进行了调整,从而实现对攻击角度的约束。表10-4~表10-6给出了4枚从弹分别采用基于弹目距离跟踪的攻击时间协同的制导律和本章提出的同时具有攻击时间约束和攻击角度约束的MPSP制导律时,各导弹的攻击角度情况。......
2023-08-02

此时,将式视为系数由t=t1时刻rmd、等量确定的线性定常系统,基于最优控制理论来设计协同制导律。由式和式可知,防御弹控制量wq与目标控制量vq的关系为由式和式可得哈密顿函数为式中,λ21和λ22为协态量,其正则方程分别为λ21和λ22在末端时刻满足的横截条件分别为式中,由式和式,可解得协态量λ21和λ22分别为式中,χ=/rmd≈-1。......
2023-08-02

针对如式所示的目标信息单向传输时的模型,类似地设计协同拦截制导律。例14-1假设目标、防御弹和攻击弹的初始位置、速度和弹道倾角同例13-1中的表13-1,3个飞行器常速飞行,攻击弹和防御弹分别采用Nm=4、Nd=4的增强比例导引律。图14-6不同防御弹制导律时qmd的变化曲线图14-7不同防......
2023-08-02
相关推荐