直流磁路计算方法分析

2023-06-30 理论教育版权反馈

【摘要】：在电磁铁结构尺寸和工作气隙值已知的情况下，直流磁路计算有以下任务。直流磁路计算可以采用分段法、漏磁系数法等方法。所分段数越多越接近于直流电磁铁的实际情况。图4-10拍合式直流电磁铁的磁动势及铁芯磁通图直流拍合式直流电磁铁示意图；线圈磁动势分态图；铁芯磁通图漏磁系数的定义及计算方法。

对于具有并联线圈的直流电磁铁，线圈电流取决于外施电压与线圈电阻的比值，即

在外施一定电压，线圈电阻不变（在稳定发热的情况下，可以认为线圈电阻不变），线圈中电流是一定的，即线圈磁动势是一定的，不随工作气隙的变化而变化。

对于具有串联线圈的直流电磁铁，线圈本身电阻很小，线圈电流等于负载电流，故线圈磁动势也不随工作气隙的大小变化。因此，直流电磁铁也称为恒磁动势电磁铁。

在电磁铁结构尺寸和工作气隙值已知的情况下，直流磁路计算有以下任务。

（1）已知工作气隙磁通值Φδ，求所需线圈磁动势IN，称为正求任务。

（2）已知线圈磁动势IN，求工作气隙磁通值Φδ，称为反求任务。

直流磁路计算可以采用分段法、漏磁系数法等方法。

1.分段法

当采用分段法计算磁路时，将铁芯及铁轭分成若干小段，假定每一小段内磁通值是相同的，漏磁通只存在于分段交界处，同时假定每一小段中的磁动势是集中的，可以用一个集中磁动势表示，图4-9（a）是单U形直动式直流电磁铁分为4段的示意图，图4-9（b）为画出的等效磁路。所分段数越多越接近于直流电磁铁的实际情况。

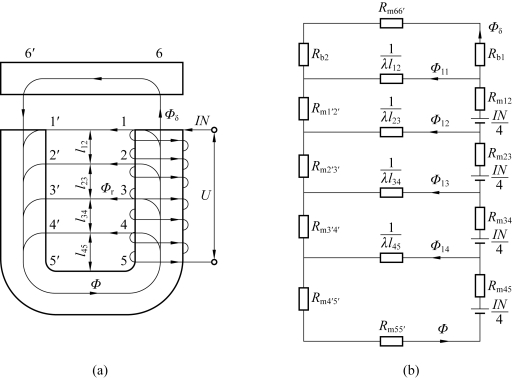
pagenumber_ebook=112,pagenumber_book=106

图4-9　分段法

（a）单U形直动式直流电磁铁示意图；（b）等效磁路

画出等效磁路图之后，先计算工作气隙磁阻Rδ1、Rδ2（工作气隙磁导的倒数）和铁芯单位长度对铁轭的漏磁导λ，再根据计算任务，用磁路的基本定律列出方程式，然后求解。等效磁路如图4-9（b）所示，漏磁通及铁磁阻均未忽略，所以计算过程中需假设一个初始值。若为正求任务，需假设一fm值；若为反求任务，需假设一Φδ值，然后逐步求解，反复计算，以逼近真值。用分段法计算磁路，分段越多，计算结果越准确，所花费的时间也越多。然而，当磁路各部分截面不等，或者单位长度漏磁导λ非常数时，应用分段法求解，不仅易行，而且有较高的准确度，同时这个方法适宜用计算机进行计算。

2.漏磁系数法

漏磁系数法是工程上常用的比较简便的磁路近似计算方法，一般情况下，也能达到工程上所需要的准确度。现以图4-10所示的拍合式电磁铁为例来说明。

pagenumber_ebook=113,pagenumber_book=107

图4-10　拍合式直流电磁铁的磁动势及铁芯磁通图

（a）直流拍合式直流电磁铁示意图；（b）线圈磁动势分态图；（c）铁芯磁通图

（1）漏磁系数的定义及计算方法。图4-10（b）表示线圈磁动势（IN）x与铁芯高度x的关系曲线，由于线圈磁动势是均匀分布的，在铁芯底面即x=0处，与漏磁交链的线圈磁动势为0；在铁芯顶面即x=li处，与漏磁通相交链的线圈磁动势是全部磁动势IN；图4-10（c）为铁芯中磁通Φx与铁芯高度x的关系曲线，由于主磁通Φδ及全部漏磁通Φl均要通过铁芯底面，故在x=0处，Φx=Φ0=Φδ+Φl，在铁芯顶面只有主磁通通过，故在x=li处，Φx=Φ0；为便于计算，将通过铁芯底面的总磁通Φ0对工作气隙磁通Φδ的比值定义为漏磁系数σ，即

pagenumber_ebook=113,pagenumber_book=107

（2）漏磁通Φl的计算方法。如图4-10（a）所示，在铁芯全长上均有漏磁通，若铁芯对铁轭单位长度漏磁导为λ，在距铁芯底面为x处，取一小段长度dx，此小段铁芯的漏磁导dΛl为

在x处与漏磁通相交链的磁通势（IN）x为

dx小段内的漏磁通为dΦl，根据磁路的基尔霍夫第二定律，并忽略铁磁阻和非工作气隙磁阻，可列出

pagenumber_ebook=114,pagenumber_book=108

从铁芯底面到顶面漏磁通总和为Φl，即

pagenumber_ebook=114,pagenumber_book=108

为了便于计算，用一个集中在铁芯顶端的集中漏磁导Λld来代替实际分布的漏磁导，用一个集中磁动势IN代替实际上分布的线圈磁动势，并忽略铁磁阻和非工作气隙磁阻，可画出等效电路如图4-11所示。

等效漏磁导Λld中通过的漏磁通为总漏磁通Φl，故称其为按漏磁通不变原则归化的等效漏磁导。漏磁通Φl也可以表示为

比较式（4-52）和式（4-53），可知

pagenumber_ebook=114,pagenumber_book=108

图4-11　拍合式直流电磁铁等效磁路

将式（4-53）代入式（4-51）中，可得出漏磁系数σ的计算公式为

用漏磁系数法计算直流磁路分为以下2种情况。

1）已知Φδ求IN

计算直流磁路的步骤如下。

（1）在已知的工作气隙值下，计算工作气隙磁导和各非工作气隙磁导及铁芯单位长度漏磁导等。

（2）用式（4-50）可计算出等效漏磁导Λld及式（4-55）可计算漏磁系数σ。

（3）计算工作气隙磁压降Uδ，可表示为

（4）计算导磁体各部分的铁磁阻压降Um及各非工作气隙磁压降Uf。

以图4-10为例，衔铁、极靴、非工作气隙中的磁通为Φδ；非工作气隙及铁轭底部的磁通可认为是Φ0，而Φ0=σΦδ；铁芯及铁轭与铁芯平行部分的磁通是变化的，可以假定其上半部磁通为Φδ，下半部磁通为Φ0。在已知各部分导磁体的磁通值及截面积时，可求出各部分导磁体内磁感应强度B，再查导磁体材料的直流磁化曲线，找出相应的磁场强度H，乘以其磁路长度l就得到各部分导磁体的磁压降Um=Hl，导磁体中总磁压降∑Um=∑Hl；非工作气隙磁压降Uf=Φ/Λf，各非工作气隙总磁压降∑Uf=∑Φ/Λf；∑Um+∑Uf称为局部磁路的磁压降。

（5）计算所需线圈磁动势IN。根据磁路的基尔霍夫第二定律，沿主磁通回路，IN可表示为

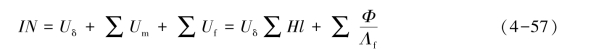
pagenumber_ebook=115,pagenumber_book=109

2）已知IN求Φδ

计算直流磁路的步骤如下。

（1）计算工作气隙磁导及各非工作气隙磁导和铁芯单位长度漏磁导。

（2）计算等效漏磁导及漏磁系数。

（3）假定导磁体的铁磁阻及各非工作气隙磁阻为0，计算Φδ的零次近似值Φδ0为

（4）假定5～6个Φδ值，即Φδ1，Φδ2，…，Φδn≤Φδ0，按上述方法计算出相应的∑Um+∑Uf，作Φδ=f（∑Um+∑Uf）曲线，如图4-12所示，称为局部磁路的磁化曲线。

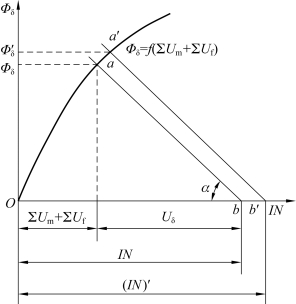
pagenumber_ebook=115,pagenumber_book=109

图4-12　用图解法求Φδ值

（5）用作图法求Φδ。在图4-12的横坐标上取Ob=IN，由点b作射线，与横坐标轴夹角为α（tanα=Λδ（n/m），其中n、m分别为横、纵坐标的比例尺），此射线与曲线的交点a的纵坐标值，即为所求的Φδ值。

若工作气隙及磁导体尺寸均不变，只把线圈磁动势改为（IN）′，则在横坐标轴上取Ob′=（IN）′，过点b′作射线平行于ab，与曲线交于a′点，此点的纵坐标即为所求的 pagenumber_ebook=116,pagenumber_book=110 值。若改变工作气隙值，则应重新计算Λδ及σ，作出新的局部磁路磁化曲线，再按以上步骤求工作气隙磁通值。

直流磁路计算方法分析

相关推荐