数字基带信号的波形分析

2025-09-29 理论教育版权反馈

【摘要】：对不同的数字基带传输系统，应根据不同信道特性及系统指标的要求，选择适当的数字脉冲波形。原则上可选择任意形状的脉冲作为基带信号波形，如矩形脉冲、三角波脉冲、高斯脉冲及正余弦脉冲等。下面就以矩形脉冲为例，介绍几种基带信号波形，如图3-10所示。此外，从信源的统计规律来看，“1”码和“0”码出现的概率相等，所以这种波形无直流分量。

对不同的数字基带传输系统，应根据不同信道特性及系统指标的要求，选择适当的数字脉冲波形。原则上可选择任意形状的脉冲作为基带信号波形，如矩形脉冲、三角波脉冲、高斯脉冲及正余弦脉冲等。但实际系统常用的数字波形易于产生和处理。下面就以矩形脉冲为例，介绍几种基带信号波形，如图3-10所示。

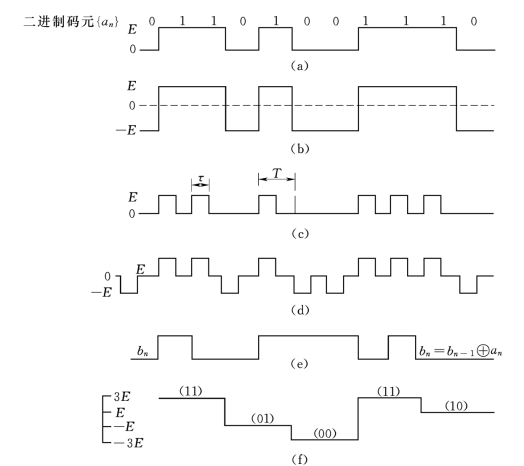
pagenumber_ebook=44,pagenumber_book=38

图3-10　几种常用的基带信号波形

（a）单极性波形；（b）双极性波形；（c）单极归零波形；（d）双极性归零波形；（e）差分波形；（f）所电平脉冲波形

1.单极性波形（NRZ）

单极性波形是一种简单的二进制数字基带信号波形。这种波形用正（或负）电平和零电平表示二进制码元的“1”码和“0”码。也就是用脉冲的有无表示码元的“1”和 “0”，如图3-10 （a）所示。这种波形的特点是脉冲的极性单一，有直流分量，且脉冲之间无空隙，即脉冲的宽度等于码元的宽度。故这种脉冲又称为不归零码（Non Return to Zero）。单极性波形一般用于近距离的电传机之间的信号传输。

2.双极性波形

在双极性波形中，用正电平和负电平分别表示二进制码元的“1”码和“0”码，如图3-10 （b）所示，这种波形的脉冲之间也无空隙。此外，从信源的统计规律来看，“1”码和“0”码出现的概率相等，所以这种波形无直流分量。同时，这种波形具有较强的抗干扰能力。故双极性波形在基带传输系统中应用广泛。

3.单极性归零波形（RZ）

单极性归零波形如图3-10 （c）所示。它的特点是脉冲的宽度τ小于码元的宽度T，每个脉冲在小于码元宽度的时间内总要回到零电平，所以称这种波形为归零波形（Return to Zero）。归零波形由于码元间隔明显，因此有利于定时信息的提取。但单极性归零波形中仍含有直流分量，脉冲变窄，码元能量减小，因而在匹配接收时，输出信噪比不归零波形的低。

4.双极性归零波形(https://www.chuimin.cn)

这种波形是用正电平和负电平分别表示二进制码元的“1”码和“0”码，但每个脉冲在小于码元宽度的时间内都要回到零电平，如图3-10 （d）所示。这种波形兼有双极性和归零波形的特点。

5.差分波形（相对码波形）

单极性波形、双极性波形、单极性归零波形和双极性归零波形中，信息码元与脉冲电平之间的对应关系是固定不变的（绝对的），所以称这些波形为绝对码波形。差分波形是把信息码元“1”和 “0”反映在相邻信号码元的相对电平变化上的波形，如图3-10 （e）所示。由图可知，差分波形中，码元“1”和 “0”分别用电平的跳变和不变来表示，即用相邻信号码元的相对电平来表示码元“1”和 “0”，故差分波形也称为相对码波形。

差分波形也可以看成是差分码序列 {bn}对应的绝对码波形，差分码bn与绝对码an之间的关系可用的编码方程表示，即

式中 ⊕——模2和运算符号。

由式（3-16）可见，当绝对码an每出现一个 “1”码时，差分码bn电平变化一次；当出现“0”码时，差分码bn电平与前一码元bn-1相同。即bn前后码元取值的变化代表了原信码an中的“1”和 “0”。

由式（3-16）可以导出译码方程为

6.多电平脉冲波形（多进制波形）

前面讲的几种都是二进制波形，实际上还存在多电平脉冲波形，也称为多进制波形。这种波形的取值是多值。代表四种状态的四电平脉冲波形，每种电平可用两位二进制码元来表示，如00代表-3E，01代表-E，10代表+E，11代表+3E，如图3-10 （f）所示。这种波形一般在高速数据传输系统中用来压缩码元速率，提高系统的频带利用率。但在相同信号功率的条件下，多进制传输系统的抗干扰性能不如二进制系统。

数字基带信号的波形分析

相关推荐