半圆盘弯曲实验的数值仿真分析

2023-06-27 理论教育版权反馈

【摘要】：使用扩展有限元方法对半圆盘弯曲实验进行计算，建立二维有限元模型如图6－16 所示。图6－16半圆盘弯曲有限元模型图6－17 所示为其开裂过程和最大主应力，图6－17 所示为初始裂纹所在位置示意，初始裂纹长度为2 mm，图6－17 和所示为裂纹扩展过程。

使用扩展有限元方法对半圆盘弯曲实验进行计算，建立二维有限元模型如图6－16 所示。模型节点数为2 438，单元数为2 362，直径是20 mm，两支撑底座间距离为16 mm，预制裂纹长度为2 mm。

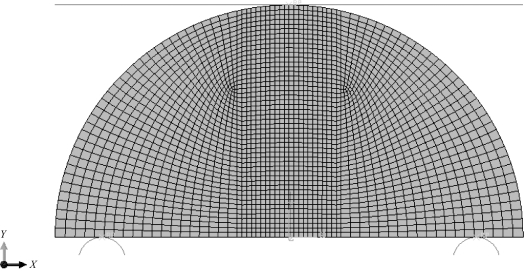
pagenumber_ebook=150,pagenumber_book=130

图6－16　半圆盘弯曲有限元模型

图6－17 所示为其开裂过程和最大主应力，图6－17 （a）所示为初始裂纹所在位置示意，初始裂纹长度为2 mm，图6－17 （b）和（c）所示为裂纹扩展过程。由图可以看出，在支撑底座处、加载处和裂纹尖端有明显的应力集中，其中裂纹尖端受到拉伸应力作用向上扩展，图6－17 （d）所示为半圆盘试样完全劈裂。

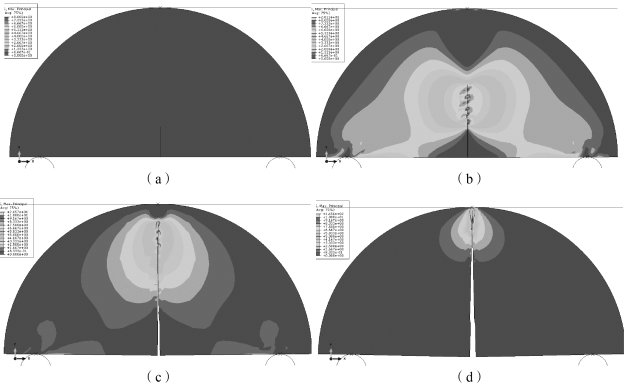
pagenumber_ebook=151,pagenumber_book=131

图6－17　半圆盘试样变形的破坏过程

（a）初始裂纹（u＝0）；（b）裂纹扩展（u＝0.047 4 mm）；（c）裂纹扩展（u＝0.09 mm）；（d）裂纹贯穿整个试样（u＝0.18 mm）

图6－18 （a）所示为加载力－加载位移曲线，加载初始阶段基本上线性增大，在加载位移等于0.072 mm 时，加载力达到最大值305 N，与文献［6］中最大加载力320 N 吻合较好。加载位移超过0.072 mm 之后迅速下降至接近于0。图6－18 （b）所示为加载力－裂纹张开位移曲线，裂纹张开位移是取初始裂纹附近两侧对称位置的点的相对位移，在张开位移等于0.058 mm 时加载力最大。

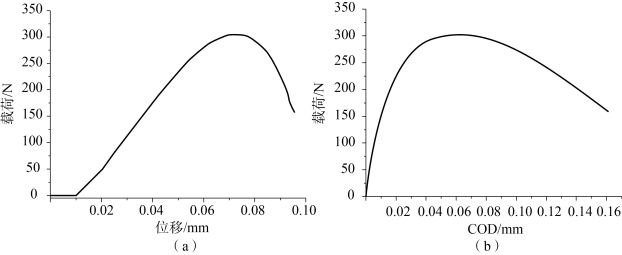
pagenumber_ebook=151,pagenumber_book=131

图6－18　加载力随加载位移和裂纹张开位移的变化曲线

（a）加载力－加载位移曲线；（b）加载力－裂纹张开位移曲线

半圆盘弯曲实验的数值仿真分析

相关推荐