如图21.9、图21.10所示,利用ABAQUS建立一个1 000 mm长的有限元模型。图21.9第一层玻纤模型图21.10内外层及基体PE部分假设每一层之间相互紧密连接,利用Extrusion命令建成模型,然后用Partition命令分割各层,并将材料属性赋予各层。......
2025-09-29
1.雷诺平均的N-S方程模拟(RANS)
雷诺平均是将湍流流动分为时均和脉动两部分,代入N-S方程进行时间平均,作为平均部分的方程组仍然保持了原有的形式,但作为脉动量之间的关联则产生了新的未知项,即雷诺应力项。雷诺平均的方法目前仍然是计算流体动力学中的最主要的方法,对雷诺平均后产生的雷诺应力的封闭模式至少有上百种,笔者仅给出几种较有代表性的模型方程,至于每个模型的应用利弊,只能在具体应用的时候根据所研究的问题,综合考虑后进行选择。如前所述,雷诺平均(RANS)的基本方程如下
式中,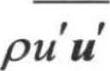 是雷诺应力项,根据对该项处理的不同,分成多种封闭模型。常用的是Boussinesq假设,雷诺应力与平均速度梯度成正比,建立如下关系
是雷诺应力项,根据对该项处理的不同,分成多种封闭模型。常用的是Boussinesq假设,雷诺应力与平均速度梯度成正比,建立如下关系
商用CFD软件基本都采用该模型,这种模型的好处在于只需求解一个方程,计算量小。但该模型将mt简化为一个各向同性标量,在一些复杂流动场合,其适用性就受到局限。下面简单介绍几组常用的湍流模型。
(1)单方程(Spalart-Allmaras)模型
单方程模型求解变量是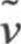 ,表征出了近壁(黏性影响)区域以外的湍流运动黏性系数。
,表征出了近壁(黏性影响)区域以外的湍流运动黏性系数。 的输运方程为
的输运方程为
式中,Gv是湍流黏性产生项;Yv是由于壁面阻挡与黏性阻尼引起的湍流黏性的减少;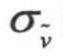 和Cb2是常数;v是分子运动黏性系数。
和Cb2是常数;v是分子运动黏性系数。
湍流黏性系数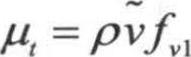 ,其中,fv1是黏性阻尼函数,定义为
,其中,fv1是黏性阻尼函数,定义为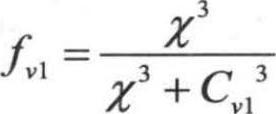 ,
,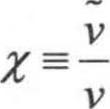 ,而湍流黏性产生项Gv模拟为
,而湍流黏性产生项Gv模拟为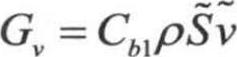 ,其中
,其中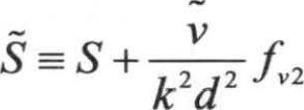 ,
,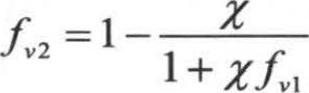 Cb1和k是常数,d是计算点到壁面的距离;
Cb1和k是常数,d是计算点到壁面的距离;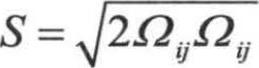 ,
,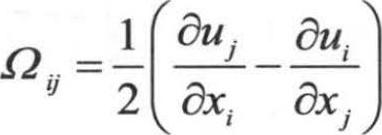 。在商用CFD软件中,考虑到平均应变率对湍流产生也起到很大作用,
。在商用CFD软件中,考虑到平均应变率对湍流产生也起到很大作用,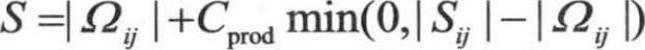 ,其中,Cprod=2.0,
,其中,Cprod=2.0,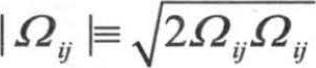 ,
,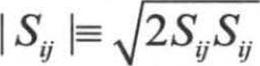 ,平均应变率
,平均应变率 。涡
。涡
在涡量超过应变率的计算区域计算出来的涡旋黏性系数变小。这适合涡流靠近涡旋中心的区域,那里只有“单纯”的旋转,湍流受到抑制。包含应变张量的影响更能体现旋转对湍流的影响。忽略了平均应变,估计的涡旋黏性系数产生项偏高。
湍流黏性系数减少项Yv为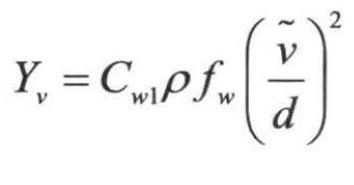 ,其中,
,其中,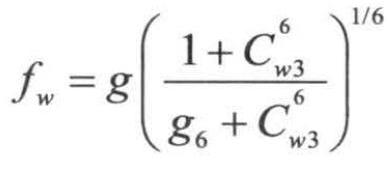 ,g=r+Cw2(r6-r)
,g=r+Cw2(r6-r) Cw1、Cw2、Cw3是常数,在计算r时用到的
Cw1、Cw2、Cw3是常数,在计算r时用到的 受平均应变率的影响。
受平均应变率的影响。
上面的模型常数在商用CFD软件中默认值为Cb1=0.1335,Cb2=0.622,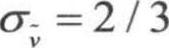 ,Cv1=7.0,
,Cv1=7.0,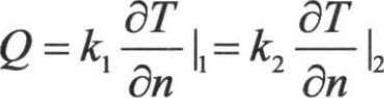 v1=v2,T1=T2,p1=p2,Cw3=2.0,k=0.41。
v1=v2,T1=T2,p1=p2,Cw3=2.0,k=0.41。
(2)标准k-ε模型
标准k-ε模型需要求解湍动能及其耗散率方程。湍动能输运方程是通过精确的方程推导得到的,但耗散率方程是通过物理推理,数学上模拟相似原形方程得到的。该模型假设流动为完全湍流,分子黏性的影响可以忽略。因此,标准k-ε模型只适合完全湍流的流动过程模拟。标准k-ε模型的湍动能k和耗散率ε方程为如下形式:
式中,Gk表示由于平均速度梯度引起的湍动能产生,Gb表示由于浮力影响引起的湍动能产生,YM表示可压缩湍流脉动膨胀对总的耗散率的影响。湍流黏性系数 。
。
在商用CFD中,一般默认常数为C1ε=1.44,C2ε=1.92,C3ε=0.09,湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0,σε=1.3。
(3)重整化群k-ε模型
重整化群k-ε模型是对瞬时的Navier-Stokes方程用重整化群的数学方法推导出来的模型。模型中的常数与标准k-ε模型不同,而且方程中也出现了新的函数或者项。其湍动能与耗散率方程与标准k-ε模型有相似的形式:
式中,Gk表示由于平均速度梯度引起的湍动能产生,Gb表示由于浮力影响引起的湍动能产生,YM表示可压缩湍流脉动膨胀对总的耗散率的影响,这些参数与标准k-ε模型中相同。ak和aε分别是湍动能k和耗散率ε的有效湍流普朗特数的倒数。湍流黏性系数计算公式为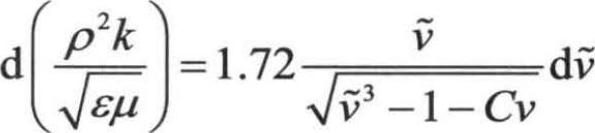 ,其中,
,其中, ,Cv≈100。对于前面方程的积分,可以精确到有效雷诺数(涡旋尺度)对湍流输运的影响,这有助于处理低雷诺数和近壁流动问题的模拟。对于高雷诺数,上面方程可以给出:
,Cv≈100。对于前面方程的积分,可以精确到有效雷诺数(涡旋尺度)对湍流输运的影响,这有助于处理低雷诺数和近壁流动问题的模拟。对于高雷诺数,上面方程可以给出: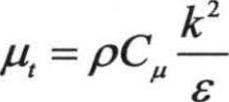 ,Cµ=0.0845。这个结果非常有意思,和标准k-ε模型的半经验推导给出的常数Cµ=0.09非常接近。在商用CFD中,如果是默认设置,用重整化群k-ε模型时是针对的高雷诺数流动问题。如果对低雷诺数问题进行数值模拟,必须进行相应的设置。
,Cµ=0.0845。这个结果非常有意思,和标准k-ε模型的半经验推导给出的常数Cµ=0.09非常接近。在商用CFD中,如果是默认设置,用重整化群k-ε模型时是针对的高雷诺数流动问题。如果对低雷诺数问题进行数值模拟,必须进行相应的设置。
(4)可实现k-ε模型
可实现k-ε模型的湍动能及其耗散率输运方程为
式中,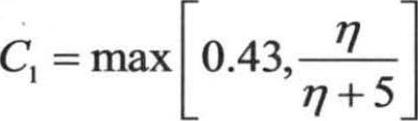 ,η=Sk/ε。
,η=Sk/ε。
在上述方程中,Gk表示由于平均速度梯度引起的湍动能产生,Gb表示由于浮力影响引起的湍动能产生,YM表示可压缩湍流脉动膨胀对总的耗散率的影响,C2和C1ε是常数,σk和σε分别是湍动能及其耗散率的湍流普朗特数。在商用CFD中,默认值常数一般取C1ε=1.44,C2=1.9,sk=1.0,sε=1.2。
该模型的湍流黏性系数与标准k-ε模型相同。不同的是,黏性系数中的Cm不是常数,而是通过公式计算得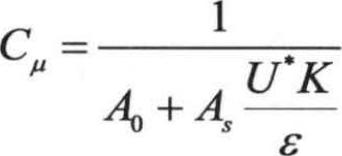 ,其中,
,其中,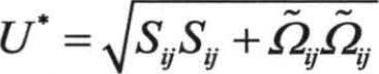 ,
,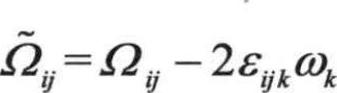 ,
,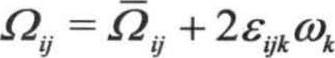 ,
,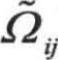 表示在角速度wk旋转参考系下的平均旋转张量率。模型常数A0=4.04,
表示在角速度wk旋转参考系下的平均旋转张量率。模型常数A0=4.04,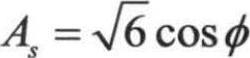 ,
, ,应变
,应变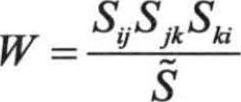 ,
,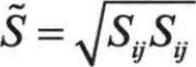 ,
,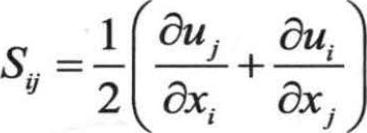 。从这些公式中发现,Cµ是平均应变率与旋度的函数。在平衡边界层惯性底层,可以得到Cµ=0.09,与标准k-ε模型中采用的常数一样。
。从这些公式中发现,Cµ是平均应变率与旋度的函数。在平衡边界层惯性底层,可以得到Cµ=0.09,与标准k-ε模型中采用的常数一样。
该模型适合的流动类型比较广泛,包括有旋均匀剪切流、自由流(射流和混合层)、腔道流动和边界层流动。对以上流动过程模拟结果都比标准k-ε模型的结果好,特别是可实现k-ε模型对圆口射流和平板射流模拟中,能给出较好的射流扩张角。
双方程模型中,无论是标准k-ε模型、重整化群k-ε模型还是可实现k-ε模型,三个模型有类似的形式,即都有k和ε的输运方程,它们的区别在于:①计算湍流黏性的方法不同;②控制湍流扩散的湍流普朗特数不同;③方程中的产生项和Gk关系不同,但都包含了相同的表示由于平均速度梯度引起的湍动能产生Gk,表示由于浮力影响引起的湍动能产生Gb,表示可压缩湍流脉动膨胀对总的耗散率的影响YM。
湍动能产生项
式中,Prt是能量的湍流普特朗数,对于可实现k-ε模型,默认设置值为0.85;对于重整化群k-ε模型,Prt=1/a,a=1/Prt=k/mCp。热膨胀系数 ,对于理想气体,浮力引起的湍动能产生项变为
,对于理想气体,浮力引起的湍动能产生项变为
(5)雷诺应力模型
雷诺应力模型(RSM)是求解雷诺应力张量的各个分量的输运方程。具体形式为(https://www.chuimin.cn)
式中,左边的第二项是对流项Cij,右边第一项是湍流扩散项CTij,第二项是分子扩散项DLij,第三项是应力产生项Pij,第四项是浮力产生项Gij,第五项是压力应变项φij,第六项是耗散项eij,第七项系统旋转产生项Fij。
式(1.3-14)中,Cij、DTij、Pij、Fij不需要模拟,而DTij、Gij、φij、εij需要模拟以封闭方程。下面简单对几个需要模拟项进行模拟。
根据用Delay和Harlow的梯度扩散模型来模拟DTij,但这个模型会导致数值不稳定,在商用CFD中采用的是标量湍流扩散模型:
式中,湍流黏性系数用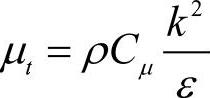 来计算,根据Lien和Leschziner,sk=0.82,这和标准k-ε模型中选取1.0有所不同。
来计算,根据Lien和Leschziner,sk=0.82,这和标准k-ε模型中选取1.0有所不同。
压力应变项φij可以分解为三项,即
式中,φij,1、φij,2和φwij分别是慢速项、快速项和壁面反射项,具体表述可以参见相关专业资料。
浮力引起的产生项Gij模拟为
耗散张量εij模拟为
式中,YM=2ρεM2t,Mt是马赫数;标量耗散率e用标准k-e模型中采用的耗散率输运方程求解。
2.直接数值模拟
将N-S方程不做任何平均,直接离散求解,称作直接模拟(DNS)。直接模拟要求网格在Kolmogorov尺度内,但一般认为最大网格尺度可以放宽到Kolmogorov尺度的15倍左右,由于N-S方程采用的假设之一是连续介质假定,此时Kolmogorov尺度分子的运动占据主导作用,但尚未达到分子运动的尺度。由于计算资源的限制,对于一些简单的湍流,直接数值模拟可以基本实现,但对于复杂的湍流,直接数值模拟仍然无法进行。
3.空间滤波的大涡模拟(LES)
大涡模拟的理论来源是Kolmogorov标度律,大涡模拟是将流动的脉动进行空间平均(滤波),对大尺度涡进行直接模拟,小尺度涡由于具有统计意义上各向同性的性质,其对大尺度涡的影响很小,因此这种方法能模拟出大尺度涡的基本特征。大涡模拟成立的前提非常严格,必须要分辨出湍流中惯性子尺度涡的一些基本特征,否则就不构成严格意义上的大涡模拟。LES模型以网格尺度为标准,将过小的时间尺度和长度尺度过滤掉,只对比网格尺度大的涡进行解析,而将比网格尺度小的涡交给亚格子尺度湍流模型模拟。所以,通过控制网格尺寸,可以控制LES对湍流的解析度,网格越密,能够解析出越小的涡。
虽然LES的计算代价相比直接数值模拟已经低很多了,但是严谨的LES计算应用在工程中的花费依然不小。因为边界层里的小尺度旋涡要求局部网格尺度足够小,否则会对边界层中的旋涡造成过度预测,比如,边界层中本该是小尺度涡主导的平静层流,计算结果却是大尺度涡主导的剧烈湍流。然而,边界层法向单维度加密网格无法解决该问题。一般,在LES模拟中网格必须三个维度同时加密才有意义,网格单元最好是立方体,即网格长宽比为1。同时要求时间步较小,平均库朗特数在0.5~1。边界层中致密的网格,网格长宽比为1的均质网格要求,较小的时间步,决定了严谨的LES计算花费也比较高。出于这个考虑,在进行LES模拟之前,最好先使用RANS和DES、SAS对问题进行研究,如果这些湍流模型不能满足要求,再使用LES。
4.分离涡模型(DES)
当需要模拟流体流经固体时的分离现象,对于大涡模拟这样的方法,边界层处的网格要布置得非常细密,对计算资源的要求也将是巨大的,于是人们想到把大涡模拟和雷诺平均进行杂交,边界层内的流动采用雷诺平均,边界层外的流动采用大涡模拟,最先由Spalart等在2025年提出。它结合了LES的湍流解析能力以及RANS模型对边界层网格的低要求,解决了LES计算花费过高和RANS模型瞬时解析不够的问题。当RANS预测的湍流尺度Lt比局部网格尺度大时,从RANS模式切换到LES模式进行计算。以SST-DES湍流模型为例,当LES模式在湍流充分发展区被激活时,局部网格尺寸D被用来计算k方程中的耗散率,来代替湍流尺度Lt:
所以,SST模型在DES中被修正为:
式中,ε是耗散率,△是最大局部网格间距△=max(△i),下标i代表第i个坐标轴),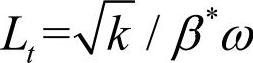 ,是湍流长度尺度,Cdes是DES方程中的标定常数,设定为0.61。
,是湍流长度尺度,Cdes是DES方程中的标定常数,设定为0.61。
在湍流充分发展区域,DES要求网格各维度均质,因为在这个区域,已经转到LES模式进行计算。在RANS区和LES区之间的区域被称为“灰色区域”,该区域网格设置不好常会给计算带来问题,所以DES在被提出之后,又出现ZonelDES、DelayedDES等改进模型。
5.尺度适应模型(SAS)
SAS湍流模型由Menter等在2025年提出,是一种改进的URANS模型,使得解析不稳定流动中的湍流谱成为可能。在湍流尺度方程中引入冯卡门长度尺度,使得SAS模型可以动态适应URANS中解析的结构,在流场中生成类似LES的成分。同时,在稳定流动部分,该模型也提供RANS求解能力。冯卡门长度尺度LvK被定义为速度矢量一阶导数除上速度导数二阶导数的绝对值,再乘以冯卡门系数k:
式中, ;
;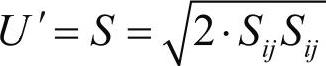 ;
;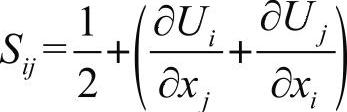 。
。
原有的SST-SAS模型已经有一些改进,其中一种便是在式(1.3-23)中使用二次长度尺度比率(L/LvK)2代替原有模型中的线性项。使用二次项使得其与模型微分更加协调,也不会与原有模型存在太大差别。另一个新的地方是,使用显式调校的高波数阻尼来满足SAS所需的频谱上高波数末端湍流阻尼要求。
最新的SAS方法一般是基于SST方程的。SST-SAS的控制方程比SST的w输运方程多一个SAS源项QSAS:
式中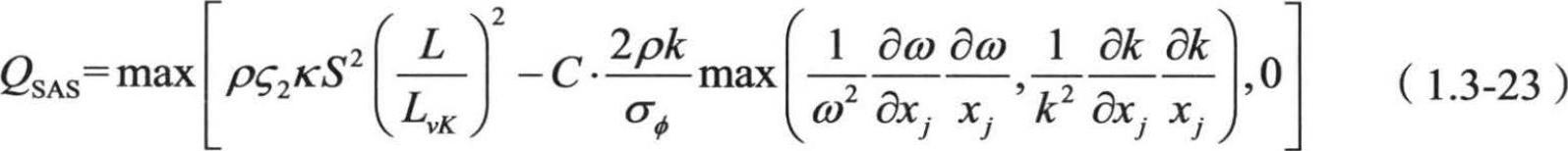
该SAS源项可从Rotta的关联长度尺度输运模型中的一项: 得出。由于在均相湍流中该积分为零,所以该值与湍流不均匀程度有关。
得出。由于在均相湍流中该积分为零,所以该值与湍流不均匀程度有关。
SAS具有RANS区不受网格间距影响的优势,所以不会像DES那样,在网格加密区计算精度下降。然而,当流动不稳定性不够强时,SAS会保持在RANS模式,不会产生不稳定结构。
相关文章

如图21.9、图21.10所示,利用ABAQUS建立一个1 000 mm长的有限元模型。图21.9第一层玻纤模型图21.10内外层及基体PE部分假设每一层之间相互紧密连接,利用Extrusion命令建成模型,然后用Partition命令分割各层,并将材料属性赋予各层。......
2025-09-29

它是由SIMPLE算法的提出人之一Patanker完成的。将上述两方面的思想结合起来,就构成了SIMPLER算法。在SIMPLER算法中,经过离散后的连续方程式用于建立一个压力的离散方程,而不像在SIMPLE算法中用来建立压力修正方程。总体而言,SIMPLER的计算效率要高于SIMPLE算法。它也是SIMPLE的改进算法之一,是由Van Doormal和Raithby提出的。......
2025-09-29

图1-21过已知点作已知直线的平行线1.3.2.2过已知点作已知直线的垂直线过已知点作已知直线的垂直线的方法如下。图1-22过已知点作已知直线的垂直线先使45°三角板的一直角边与BC重合,再使其斜边紧靠另一三角板,如图1-22所示。图1-25已知外接圆求作正五边形1.3.2.6作圆内接任意正多边形作圆内接任意正多边形的方法如下。......
2025-09-29

为了获得既满足使用性能要求,质量又稳定的涂层,必须对影响涂层性能的关键因素进行优化设计,了解其影响规律,找到影响涂层质量稳定性的关键因素,并加以严格控制。因此,涂层制备工艺优化设计是涂层开发的必经阶段。表4-4 传统试验法与统计试验法的比较下面以筛分设计为例对涂层制备工艺的优化进行介绍,关于其他设计方法可参阅相关的参考文献。......
2025-09-29

感应线圈是传递感应电流的部件,感应线圈设计的好坏对加热影响很大。在生产中,为感应钎焊特定接头而设计的感应线圈,尤其是对复杂形状接头的线圈设计,需要依靠经验并经试验而定。感应线圈与焊件之间应保持间隙以避免短路,为了提高加热效率,感应线圈应制成与钎焊的接头相似的形状,并与焊件保持不大于3mm的均匀间隙。感应线圈的匝间距离一般为管径的0.5~1倍,应尽可能采用外热式感应线圈,它比内热式感应线圈的加热效率高。......
2025-09-29

LM3445的工作频率高、调光速度快,无闪烁、浅光出现,因此,对变压器的主要参数设计要求高。计算变压器二次绕组匝数计算变压器气隙2.方法二变压器的设计方法有多种,计算结果不尽相同,但要求误差不能太大,否则,不知哪种结果正确。......
2025-09-29
相关推荐