5.2.1.2模型参数计算方法在式、式中， 为河道的泥沙综合恢复饱和系数，它与河道断面形态，冲淤状态及水流泥沙运动参数有关，βs为反映断面流速和输沙不均匀分布的系数。......
2025-09-29
风力机数学模型的优化方案
【摘要】：在风力发电系统中，风力机风能捕获的过程直接决定了风力发电系统的风能利用效率。三叶片风力机叶尖速率比的典型值为8～10。定桨距风力机的优点是控制较为简单，其缺点是叶片结构复杂、笨重、整体效率较低。变桨距风力机是另外一种风力机，其与定桨距风力机的不同之处在于其可通过改变桨叶节距角来充分利用风能。图5-34 风力机的风能利用系数C特性曲线
在风力发电系统中，风力机风能捕获的过程直接决定了风力发电系统的风能利用效率。在风速恒定的情况下，风轮产生的机械功率可表示为
式中，Pwt为风轮捕获的风能；ρ为空气密度；R为风轮扫过的面积；v为风速；Cp（λ，β）为风能利用系数，是风轮机叶尖速率比λ和桨距角β的非线性函数。
风能利用系数通常可用下式来计算[136]
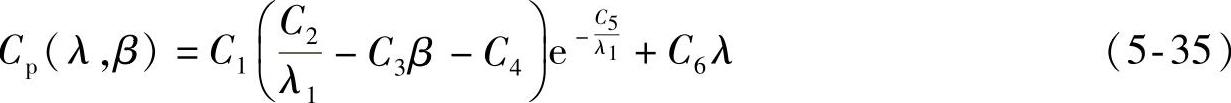
式中
式中，C1=0.5176，C2=116，C3=0.4，C4=5，C5=21，C6=0.0068。(https://www.chuimin.cn)
叶尖速率比λ为风轮叶尖线速度和风速的比值，即
λ=Ω lR/v （5-37）
式中，Ω l为风轮的转速。
三叶片风力机叶尖速率比的典型值为8～10。叶尖速率比影响风力发电机的风能利用系数，如图5-34所示。
风力机主要分为定桨距和变桨距两种。定桨距风力机的特点是桨叶与轮毂的连接是固定的，当风速变化时，桨叶的迎风角度不能随之改变，只能利用桨叶翼型本身的失速特性，在风速高于额定风速时，降低效率，自动将功率限制在额定值附近。桨叶的这一特性，通常称为自动失速性能。因而，对于这类风力机而言，当风速改变时，不能通过调整桨叶的节距来改变气流对叶片的攻角，从而改变风力机组获得的空气动力转矩而保持输出功率稳定，而只能依靠改变发电机转速来调节风电机组功率，因而定桨距风力发电机组属于变速恒频风力发电系统。定桨距风力机的优点是控制较为简单，其缺点是叶片结构复杂、笨重、整体效率较低。变桨距风力机是另外一种风力机，其与定桨距风力机的不同之处在于其可通过改变桨叶节距角来充分利用风能。在一定风速范围内，通过桨距（气流对叶片的攻角）控制而维持风机转速的稳定，而在风速过大时，除了对桨叶进行节距控制外，还通过控制发电机转子电流来控制发电机转差率，使发电机转速在一定范围内能够快速适应风速的变化，从而使输出功率更加平稳。由于变桨距风力发电系统中，风力机转速在一定风速范围内可维持恒定，并能得到恒频的电能，因而可构成恒速恒频风力发电系统。
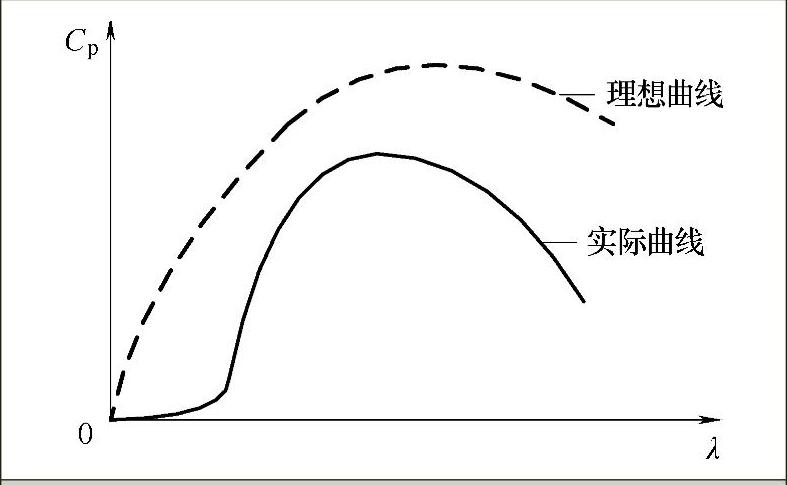
图5-34 风力机的风能利用系数C特性曲线
相关文章
- 详细阅读
-
数学模型预测结果的优化详细阅读
计算结果从定性上与相应河段模型试验结果一致，定量上略有差别。小浪底水库调节后，出库沙量大幅度下降，特别是大于0.025m 的中、粗沙大部分被拦截在库区。......
2025-09-29
-
全沙数学模型的建立与优化详细阅读
10.4.2.4沉降系数确定图10-16航道疏浚深度与悬沙沉降系数的关系在悬沙不平衡输沙方程和河床变形方程式中，沉降系数α 对河床冲淤强度有较大影响。......
2025-09-29
- 详细阅读
-
风力发电数学模型优化详细阅读
式中 vs——风力发电机的启动风速,m/s；vc——风力发电机的截止风速,m/s；vi——第i时刻的风速,i=1,2,…,n,且vs≤vi,vi+1≤vc；Pi——风速功率曲线对应风速为vi时风力发电机输出的功率,kW。......
2025-09-29
-
尼迈亚电弧的简单数学模型优化详细阅读
简单的尼迈亚模型是一种经验公式类型的电弧数学模型，按图8-1所示，断路器开断过程可分成4个过程，它们是1）瞬动电磁铁动作过程；2）电弧停滞过程；3）电弧运动过程；4）电弧进入电弧栅片熄灭过程。经过停滞阶段后，电弧开始运动，迅速从动触头转移到导弧板，并在磁场力的作用下向栅片运动，计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型，这里介绍尼迈亚模型，它由L.Niemeyer博士于1984年提出[1]。......
2025-09-29
-
数学模型计算结果优化详细阅读
图13-24异重流潜入位置变化过程表13-7水库运用初期1～5年库区输沙计算结果图13-24异重流潜入位置变化过程表13-7水库运用初期1～5年库区输沙计算结果在相同的水沙条件及边界条件下进行的小浪底库区实体模型试验结果表明，距坝67km 以下库段总淤积量为29.44 亿m3，若淤积物干容重γ0=1.15t/m3，则淤积量为33.8亿t。......
2025-09-29
-
衬底解取向优化方案详细阅读
一般来说，衬底表面的形态决定着生长机制。当表面平面相对于普通晶面发生解取向时，表面由许多台阶组成。利用MOVPE，高温生长促使原子向表面和由台阶构成的位错扩散。图2-12所示的为蓝宝石解取向角θ不同时GaN表面的演化。θ约为0.3°时，表面变得更光滑。隆起物的平均高度为5nm。图2-13 GaN在蓝宝石上生长的AFM图像，解取向角分别为θ=0.15°及θ=0.31°注：隆起物（左图）是因围绕螺旋位错的螺旋生长形成的。......
2025-09-29
相关推荐