由于STM能够直接观察到原子在物质表面的排列状态和跟表面电子行为有关系的物理化学性质，因此，STM对表面科学、材料科学、生命科学和微电子科学技术的研究都有着重大的意义和广阔的应用前景。如图3-53为各种纳米材料的SPM图像，利用仪器的软件分析，可得到纳米材料的粒径分布等信息。在纳米尺度上进一步研究材料的特性，相位成像技术不可缺少。图3-54为利用STM对Fe原子与CO分子逐步进行反应的实时观察过程。......
2025-09-29
自适应除噪：9.7WO-LMS的应用探究
【摘要】：分别用传统LMS算法和ap1nsd WO-LMS算法进行自适应除噪，模拟条件如下：1）滤波器阶数N=4。图9-17 k=0.6和k=1.0时WO和LMS除噪学习曲线（续）图9-17给出了相关度为60%和100%时的除噪曲线。然而，WO-LMS算法的优点随相关的减弱而变的越来越不明显。图9-18 稳态均方误差关于相关性变化曲线由图9-18可知，k小于0.3时，LMS具有最小的稳态误差；k大于0.3后，ap1d的稳态误差小于传统LMS算法；相关性大于0.7时，ap1nsd WO-LMS算法的稳态误差都低于LMS；ap1d特性好于ap1nsd，ap1n的性能最差。
自适应除噪（ANC）系统的原理图如图9-16所示。
在ANC中通常假定参考通道噪声nr（n）是由主通道噪声nm（n）经过一个传递函数为H（z）的系统的输出，自适应除噪的本质就是通过自适应算法估计出H（z）的逆，用nr（n）逼近d（n）=s（n）+nm（n），而有用信号与噪声不相关。实际上自适应算法是用nr（n）去逼近nm（n），得到nm（n）的估计值⌒nm（n），再与主通道d（n）相减以达到最大限度地消除主通道噪声nm（n）以获得有用信号s（n）。自适应滤波器的权系数是由逼近误差为e（n）通过LMS准则进行反馈调整。由图9-16可知系统的输出e（n）为：
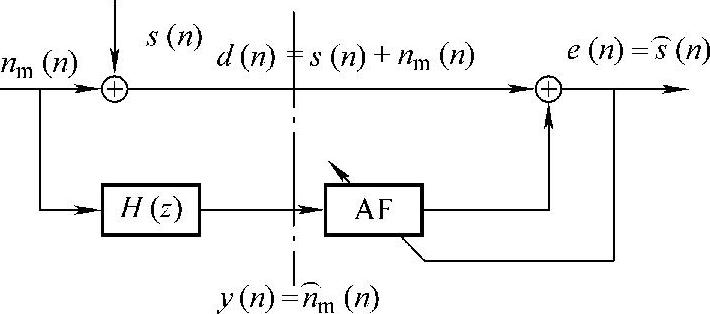
图9-16 ANC原理图
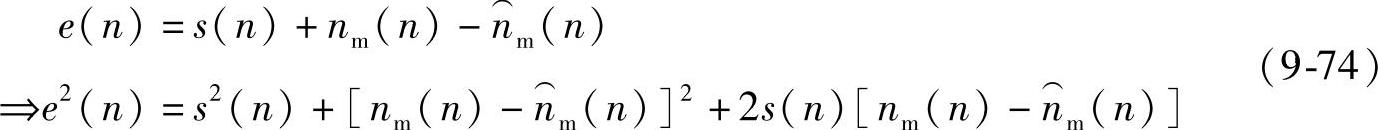
两边取数学期望，由于s（n）与nm（n）和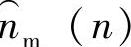
均不相关，所以有
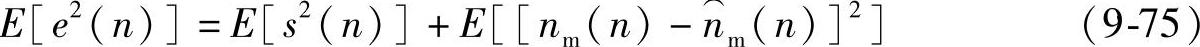
信号功率E[s2（n）]与自适应滤波器的调节无关，故自适应调节使E[e2（n）]最小就是使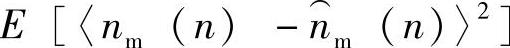
最小。由式（9-74）可知，
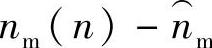（n）=e（n）-s（n），当
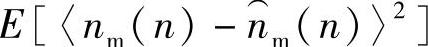最小时E[<e（n）-s（n）>2]也最小，即自适应噪声抵消系统的输出信号e（n）与有用信号s（n）的均方误差最小。可以证明，自适应滤波器能完成上述任务的必要条件为：参考输入信号nr（n）必须与被抵消的信号nm（n）相关。在图9-16系统中，nr（n）是nm（n）通过一线性系统的输出，所以收敛条件满足。
分别用传统LMS算法和ap1nsd WO-LMS算法进行自适应除噪，模拟条件如下：
1）滤波器阶数N=4。
2）信号s（n）=sin（2nπ/200）。
3）主通道噪声nm（n）是均值为0，方差为1的高斯白噪声。
4）参考噪nr（n）经过传递函数H（z）=k+（1-k）z-1（0≤k≤1）得到，k是参考噪声与主通道噪声的相关程度系数。(https://www.chuimin.cn)
实验进行2000次迭代，收敛步长μ=0.002。实验结果如图9-17所示（横坐标表示迭代次数，纵坐标为误差幅值）。
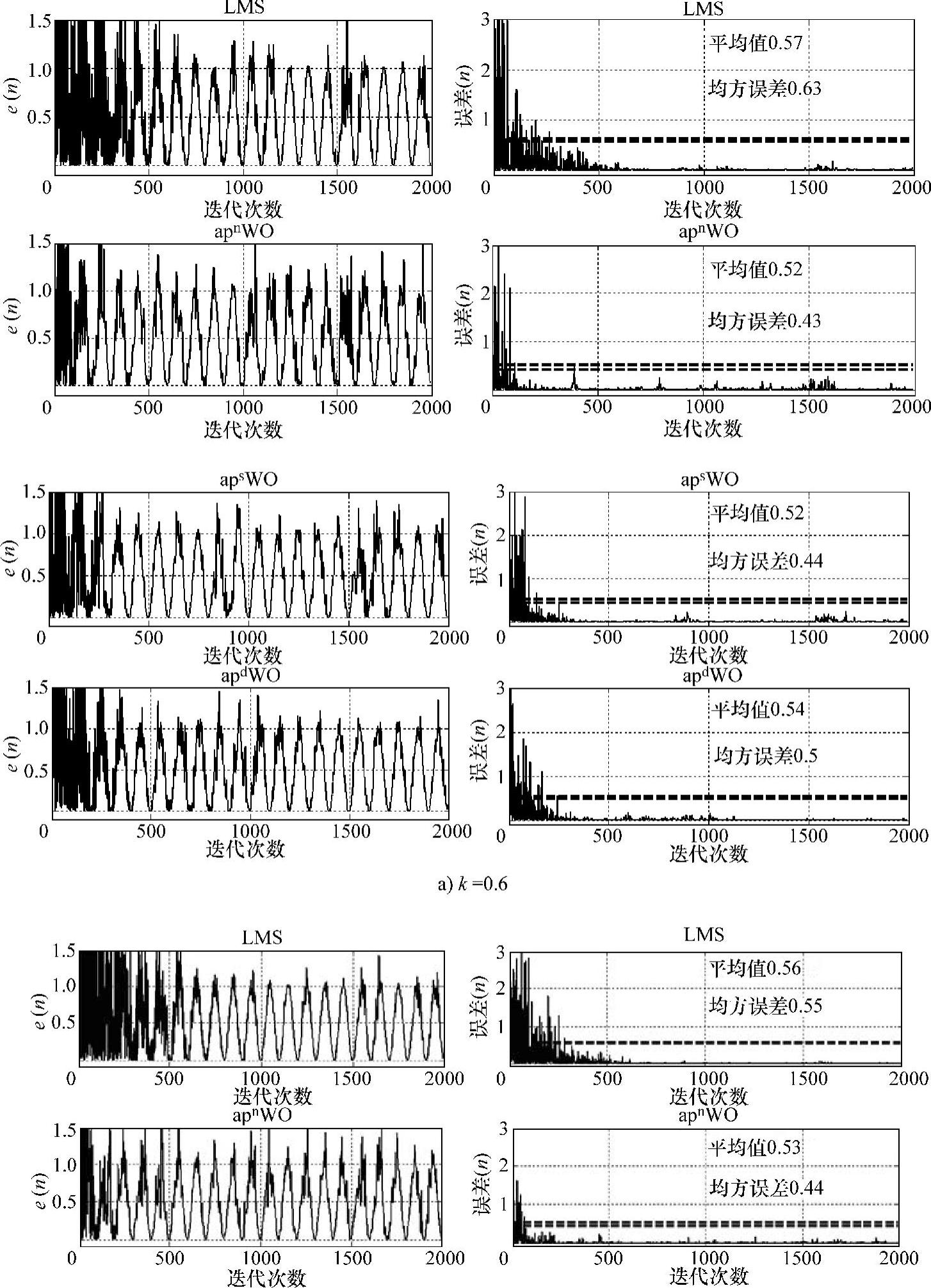
图9-17 k=0.6和k=1.0时WO和LMS除噪学习曲线
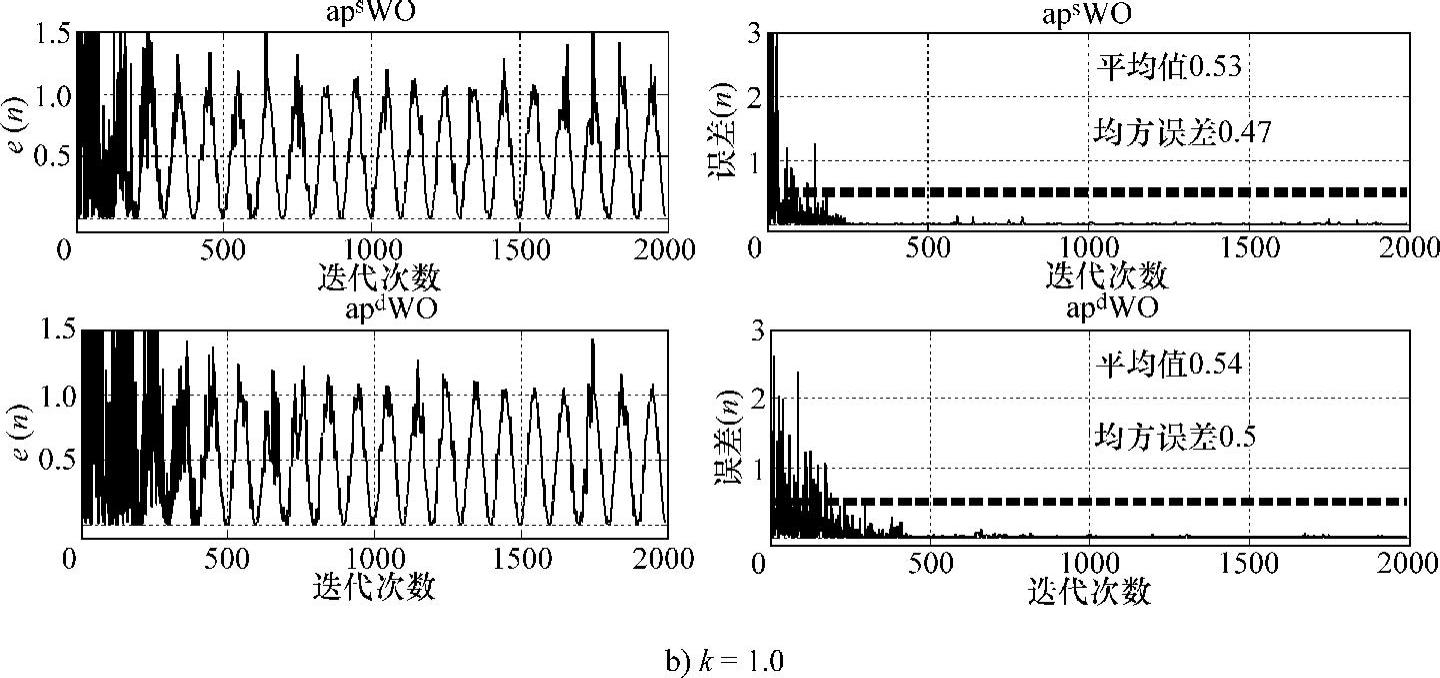
图9-17 k=0.6和k=1.0时WO和LMS除噪学习曲线（续）
图9-17给出了相关度为60%（图9-17a）和100%（图9-17b）时的除噪曲线。从图中可以看出，ap1ns WO-LMS的收敛速度明显大于LMS，ap1d收敛速度低于ap1ns，但稳态误差明显好于ap1ns和LMS；当相关性由60%变为100%，收敛速度和稳态误差均得到改善。然而，WO-LMS算法的优点随相关的减弱而变的越来越不明显。在收敛速度基本相同的条件下，WO-LMS3种算法得到的稳态误差随相关性的减小而递减。图9-18给出了各种算法的变化规律。
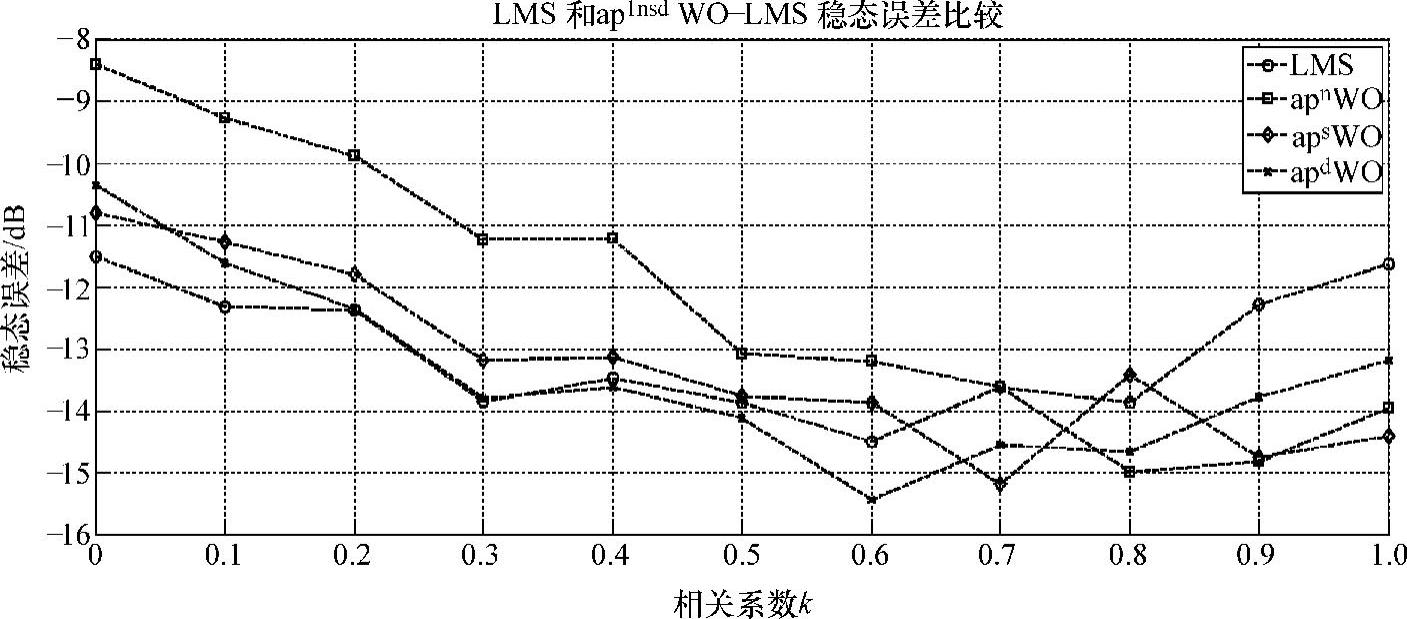
图9-18 稳态均方误差关于相关性变化曲线
由图9-18可知，k小于0.3时，LMS具有最小的稳态误差；k大于0.3后，ap1d的稳态误差小于传统LMS算法；相关性大于0.7时，ap1nsd WO-LMS算法的稳态误差都低于LMS；ap1d特性好于ap1nsd，ap1n的性能最差。上面实验的MAT- LAB代码如下：
相关文章
- 详细阅读
-
除渣精炼方法及应用研究详细阅读
杂质的来源和产生时期各不相同，在熔体内的分布状态也千差万别，合金在浇注前必须进行除渣精炼才能获得性能优良的铸件或铸锭。除渣精炼方法主要有静置澄清法除渣、浮选法除渣和溶剂除渣。除渣用溶剂由42%的硼砂、8%的碳酸钠、50%的焦炭粉混合而成，该精炼剂的密度小，熔点低，在熔炼下料时即与炉料一起加入。熔炼时，精炼剂加入量为炉料总重的0.1%～0.15%左右。使用结果表明，加入熔剂熔炼1.2t黄铜产生24.3kg的铜渣，与不加熔剂比较，减少了21.55kg。......
2025-09-29
-
自适应滤波器在实际应用中的作用详细阅读
自适应滤波器的应用主要有以下3种形式：1）如图9-1所示的联合过程估计。这种自适应滤波器常用于ADPCM语音编码。接收端利用同样的自适应滤波器得到y，然后加上接收到的e即得x。其中自适应滤波器的作用是估计输入信号的统计特性，这种自适应滤波器应用于声码器。自适应滤波得到声音信号的参量，通信中只传输参量。图9-2 自适应预测图9-2 自适应预测图9-3 自适应参数估计图9-3 自适应参数估计......
2025-09-29
-
应用扫描电镜探究纳米材料属性详细阅读
1.纳米材料的形貌观察及尺寸表征扫描电镜在纳米领域中可替代人类眼睛进行各种观察，如对纳米材料、纳米结构及纳米电子电路等进行观察记录，已经在纳米材料、纳米生物、纳米化学、纳米电子学、纳机电系统等各个领域得到了广泛的应用。......
2025-09-29
-
短纤非织造土工布的性能分析与应用探究详细阅读
短纤针刺非织造土工布的品种由生产部门根据市场需求设定。短纤针刺非织造土工布规格以标称断裂强力表示，幅宽为辅助规格，按合同规定和实际需求设定。......
2025-09-29
-
市场应用分析：探究商机与发展趋势详细阅读
根据激光扫平仪的工作原理，大致可将扫平仪分成三类：水泡式激光扫平仪、自动安平激光扫平仪和电子自动安平扫平仪。激光二极管2发出的激光，经物境1后得一激光束，该激光束再经五角棱镜6后，分成两束光线，一束直接通过，另一束改变90°方向，仪器的旋转头由电动机4通过传动带3带动旋转，使形成一个扫描的激光平面，仪器上设置有长水准器5，用于安平仪器。......
2025-09-29
-
探究立体投影技巧与应用介绍详细阅读
3-6求半圆球的水平投影及表面上线的投影。3-7分析下列各平面立体的截交线，根据它们的两面投影求第三面投影。3-12画出第三视图，并分析题与题、的对应关系。3-14补画出相贯线的正面投影。3-28补全柱锥相交的水平投影。3-30补全半球被柱面挖切后的正面和侧面投影。......
2025-09-29
- 详细阅读
相关推荐