改进直接法的方法

2023-06-23 理论教育版权反馈

【摘要】：直接法估计出的谱的方差特性不好，当数据长度N太大时，谱曲线起伏加剧，N太小时，谱峰的分辨率又不好，因此需要加以改进。上面3种改进方法可归纳为图6-3。图6-3 3种改进方法的框图古典谱估计，不论是间接法还是直接法，都可用FFT快速实现，且物理概念明确，因而仍是目前较常用的谱估计方法。实现上述直接法、间接法和三种改进的直接法谱分析的M

直接法估计出的谱的方差特性不好，当数据长度N太大时，谱曲线起伏加剧，N太小时，谱峰的分辨率又不好，因此需要加以改进。其中一种有效的方法是平均法，它的指导思想是把一长为N的数据x_N（n）分成L段，分别求每一段的功率谱，然后予以平均，常用的方法有Bartlett法、Welch法、Nuttall法等。

1.Bartlett法

将采样数据x_N（n）分成L段，每段长度都是M，第i段数据加矩形窗后为

xⁱ_N（n）=x_N[n+（i-1）M]d₁（n+（i-1）M） 0≤n≤M-1，1≤i≤L （6-4）

式中，d₁（n）是长度为M的窗口。分别计算每一段的功率谱：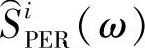

把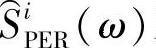对应相加后再取平均即得到平均周期图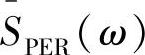为

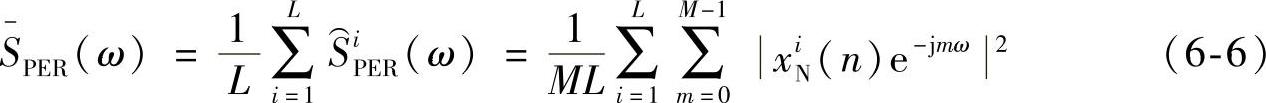
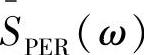的均值为

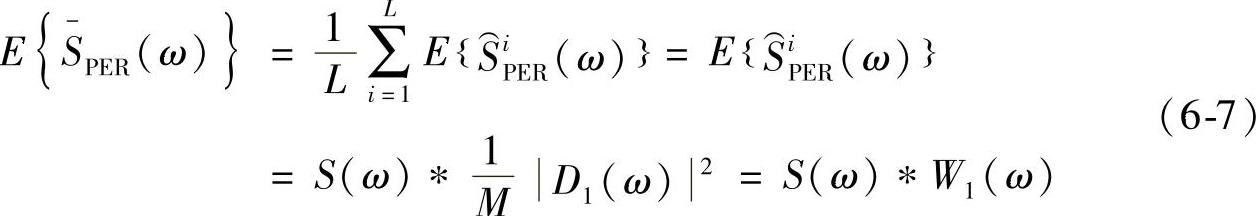
式中，D₁（ω）是矩形窗的频谱，W₁（ω）是由矩形窗做相关所得到的长为2M-1的三角窗频谱。显然，不取平均的周期图和取平均后的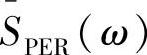都是有偏估计，且当N→∞时，两者是渐近无偏的。

2.Welch法

Welch法是Barlett法的改进。第一个改进是对x_N（n）进行分段时，可允许每一段的数据有部分的交叠。例如，每一段数据重合一半时的段数为

式中，M仍然是每段的长度，如图6-2所示。

第二个改进是每段的数据窗口可以不是矩形窗，例如使用汉宁窗或汉明窗，这样可以改善由于矩形窗旁瓣较大所产生的谱失真。这样得到的谱也是渐近无偏的，且由于允许重叠，使估计的方差得到很大的改善。

图6-2 Welch法的分段

3.Nuttall法

由于Welch法允许分段时重叠，这样就增加了段数L，当然也就增加了做FFT的次数。如果用的数据窗是非矩形窗，这又大大增加了做乘法的次数。因此，Welch法的计算量比较大。Nuttall等人提出了一种五步结合算法，具体步骤如下：

步骤1和2：与Bartlett法相同，即对x_N（n）自然分段（加矩形窗），且不交叠，得到平均后的功率谱。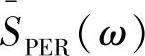

步骤3：由作反变换，得到该平均功率谱对应的自相关函数，记为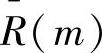，其最大宽度是2M-1，M=N/L。

步骤4：同间接法，对R^-（m）加延迟窗v₁（m），v₁（m）的最大单边宽度为M，这样得到。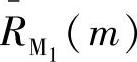

步骤5：由R-M1（m）作正变换，得到对x（n）功率谱的估计，记为S-PBT（ω）。

显然，这种方法是把直接法和间接法结合起来，同时把平滑和平均结合了起来，它既保持了平滑和平均减少方差的优点，而且计算量也较小。

上面3种改进方法可归纳为图6-3。

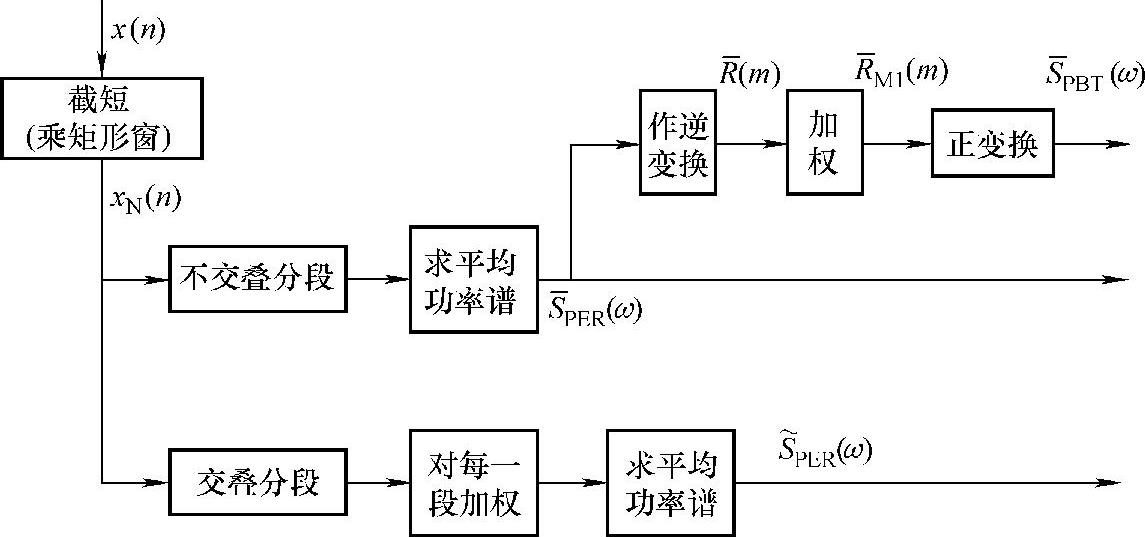
图6-3 3种改进方法的框图

古典谱估计，不论是间接法还是直接法，都可用FFT快速实现，且物理概念明确，因而仍是目前较常用的谱估计方法。但它有一些严重的缺点：

1）谱的分辨率低，它正比于2π/N，N是所使用的数据长度；

2）由于不可避免的窗函数影响，使得真正谱S（ω）在窗口主瓣内的功率向旁瓣部分“泄漏”，降低了分辨率。较大的旁瓣有可能掩盖S（ω）中较弱的成分，或是产生假的峰值。当分析的数据较短时，这些影响更为突出。

3）方差性不好，不是S（ω）的一致估计且N增大时谱曲线起伏加剧。

周期图的平滑和平均是和窗函数的使用紧紧相关联的。平滑和平均主要是用来改善周期图的方差性能，但往往又减小了分辨率和增大了方差。没有一个窗函数能使估计的谱在方差、偏差和分辨率各个方面都得到改善。因此，使用窗函数只是改进估计质量的一个技巧问题而不是根本的解决办法。

实现上述直接法、间接法和三种改进的直接法谱分析的MATLAB代码如下：

运行结果如图6-4所示。

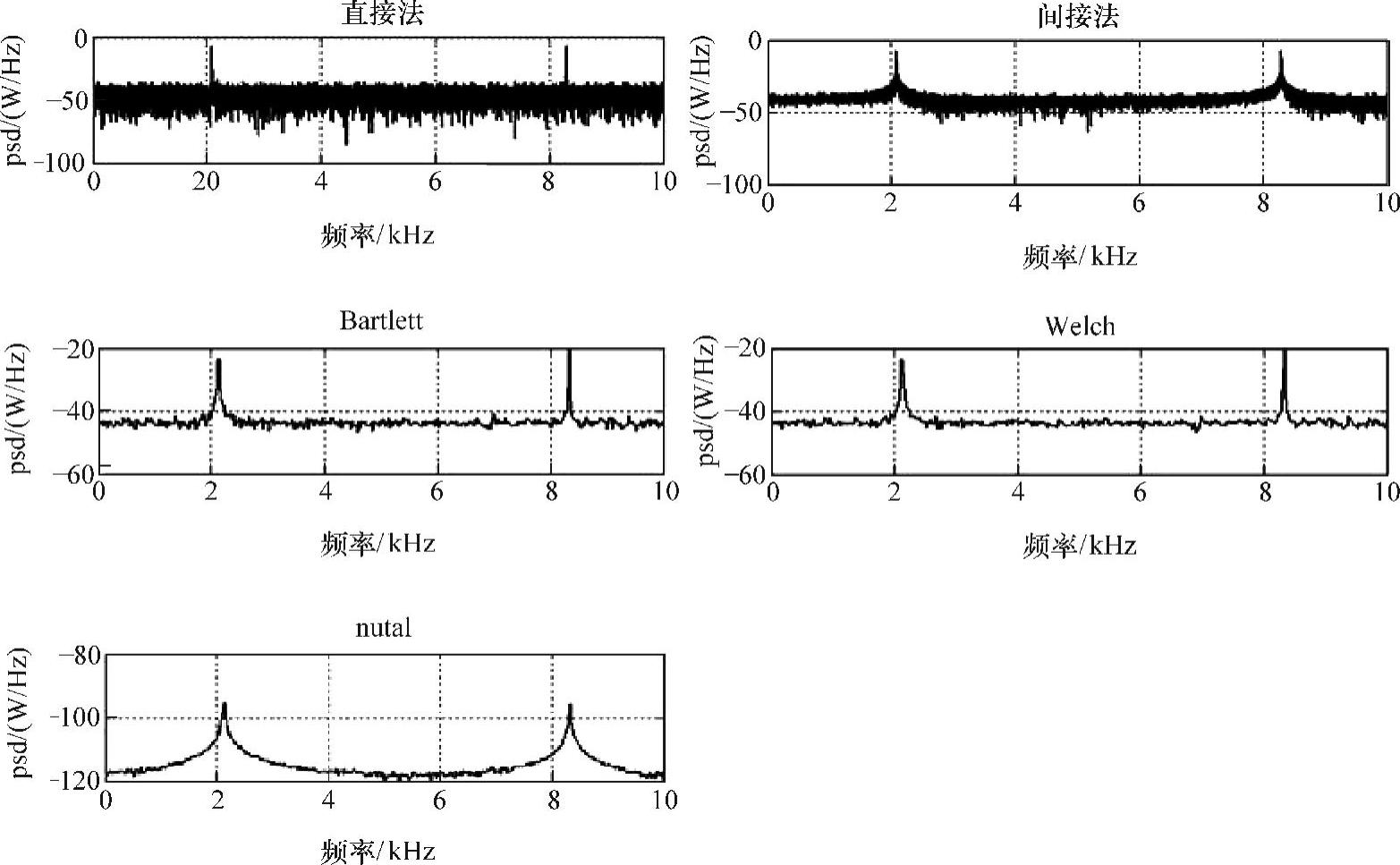
图6-4 传统谱分析结果

图6-4中的Welch方法采用矩形窗加权并按照50%重叠，Nuttal也采用矩形窗加权。观察图6-4，采用Nuttall方法得到的谱图具有最优的平滑性但旁瓣泄漏也最大；直接法和间接法由于在整个信号区间进行分析，因此旁瓣影响最小，但噪声谱干扰也比较大，因此其方差最大。在频率分辨率方面，不论直接法和间接法还是分段法都使用相同的频率取样率f_s和数据长度（N=LM），所以各种方法具有相同的频率分辨率，但实际上考虑到分段时L的取整，Bartlett、Welch和Nut_- tall三种方法的频率分辨率大于直接和间接法。

改进直接法的方法

相关推荐