为寻找更为理想的基窗函数，借助LMS算法思想提出了“基于LMS准则以apSW为模型的基窗函数设计方法”。图3-21 余弦基神经自适应网络图3-21 余弦基神经自适应网络图3-22 apSW基窗LMS设计算法按照流程图，设计截止频率为π/4的32阶低通apSW的窗函数F。......
2023-06-23
最小二乘基窗设计算法优化
【摘要】：图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性实现上述结果的MATLAB代码如下：图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性实现上述结果的MATLAB代码如下：卷积窗C性能参数B=0.2165，A=-14dB，D=-10.15dB。对比图3-16七种基窗可看出，利用最小二乘得到的基窗综合性能最好。此外，基于此结果基窗F的滤波器具有最小的均方误差。
由第2章内容可知，对于满足线性条件ap系统传输特性可表示为式（2-51），令
重写传输特性如下
假设频率取样序列为H，则传输特性的频率偏差距离为
假设N为奇数（偶数同法可证），根据卷积窗中心对称性整理式（3-31）得
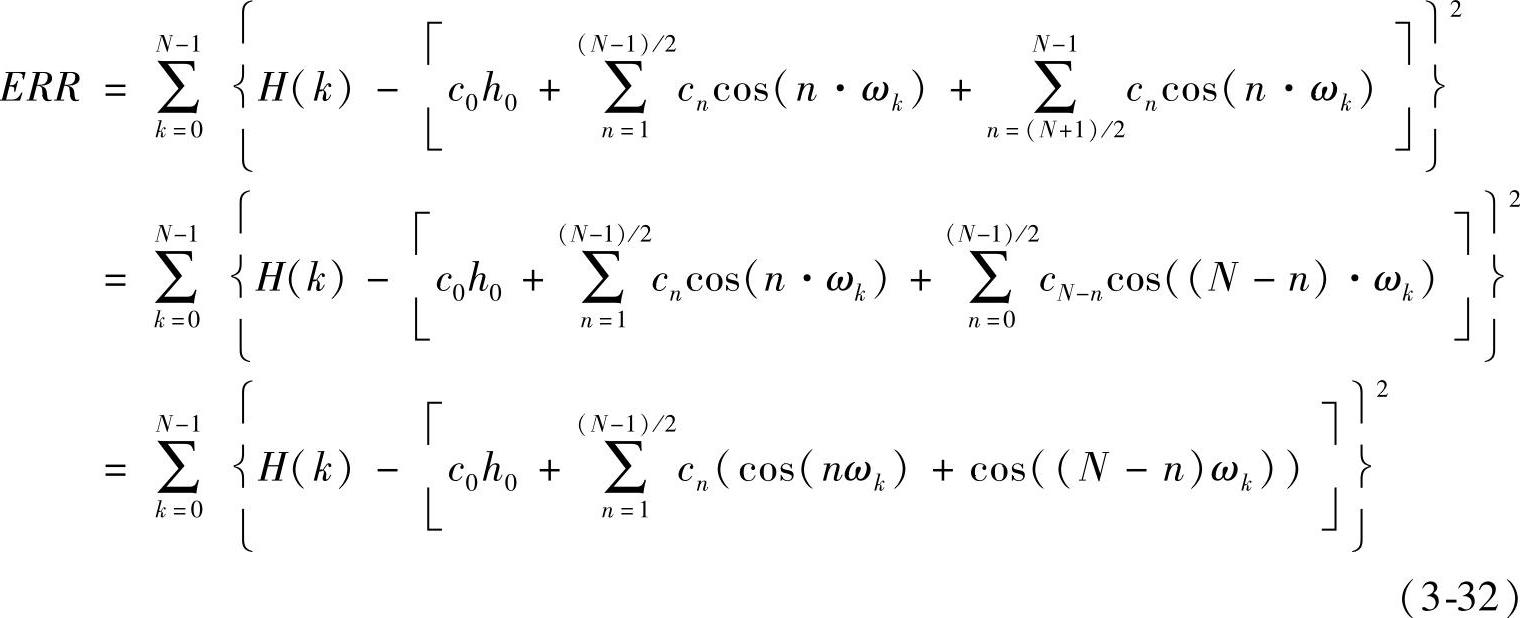
式中，ωk=2kπ/N。再令
则式（3-32）表示的频采误差又可表示为
由于H具有对称性，所以式（3-34）进一步简化如下：
式（3-35）是卷积窗C的函数，为取得最小值，应满足：
即误差对于任意卷积窗元素cn的偏导数恒为零，整理式（3-36）得：
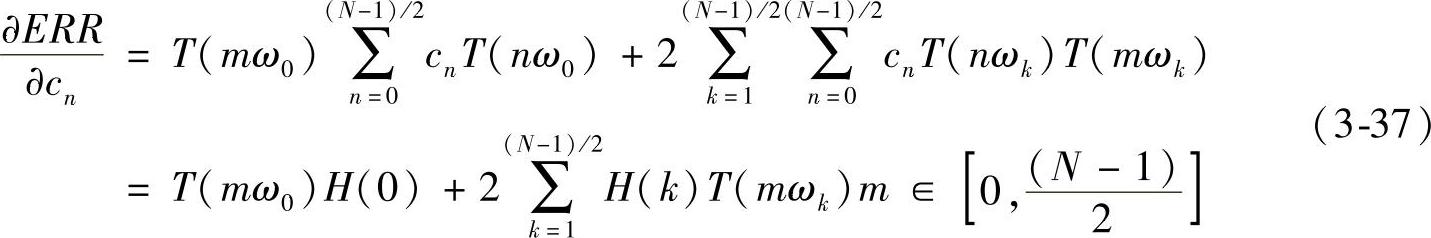
定义如下矩阵：
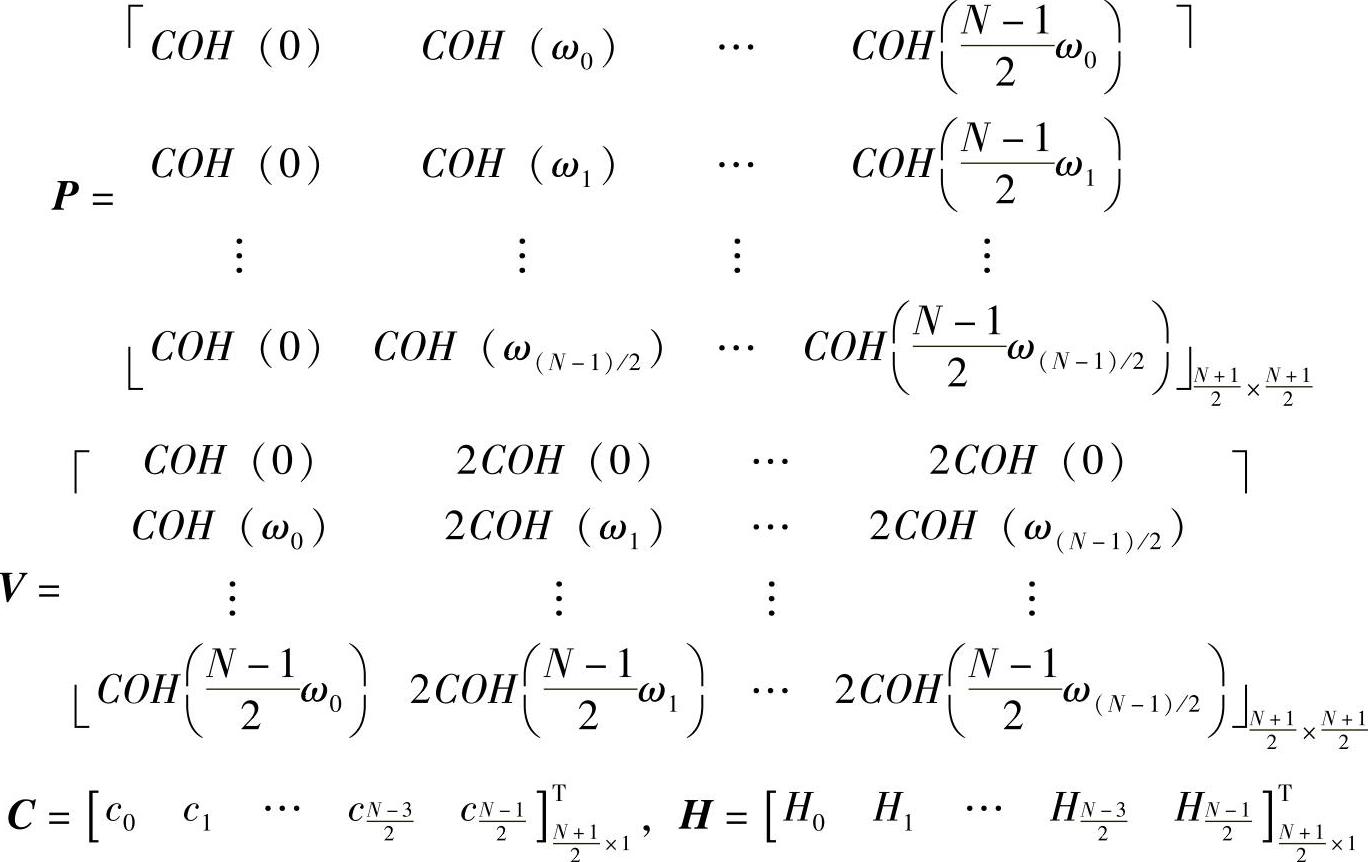
则式（3-37）的矩阵表达如下：
VPC=VH （3-38）
从而求得卷积窗C为
C=（VP）-1VH （3-39）
假设N=17的低通滤波器上截止频率为π/2，则传输特性序列H=[1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1]，其频率取样ωk=2kπ/17。求得单位响应序列h=[0.52940.3188-0.0299-0.10750.03150.0660-0.0346-0.04880.0398 0.0398-0.0488-0.03460.0660 0.0315-0.1075-0.02990.3188]，则分别构造矩阵P、V、C、H代入式（3-39）求得窗C=[0.50 0.50 0.50 0.50 0.50 0.50 0.50 0.50 1.00 0.50 0.50]，如果以C为基窗，则卷积窗图形及对应的系统曲线如图3-31所示。
图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性
实现上述结果的MATLAB代码如下（画图部分省略）：
卷积窗C性能参数B=0.2165，A=-14dB，D=-10.15dB。虽然A和D较低，但过渡带宽度降低很多，窗口速度sw达到了64.67，加速度aw达到了46.89。对比图3-16七种基窗可看出，利用最小二乘得到的基窗综合性能最好。此外，基于此结果基窗F的滤波器具有最小的均方误差。由图3-31特性曲线可看出，虽然通带幅度未达到1且阻带幅度触底到0，但系统整体误差为0.2117，比已知最优三角窗仍降低了2%。
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
基于矩形二叉分解的基窗优化设计详细阅读
基于此提出了“基于矩形窗二叉分解的基窗设计”算法，对各级分解得到的基窗使apDW特性在性能A和B之间有了较大的灵活选择性。这样，F可由若干级二叉分解基窗卷积生成，即式中，Rjni表示第j级第i个二叉分解右分支中长度等于ni的窗函数，最终可分解成若干个长度为2的矩形窗卷积，只进行1级分解的结果F就是三角窗。......
2023-06-23
-
最小均方LMS算法优化方案详细阅读
按照自适应滤波系数矢量的变化与梯度矢量方向之间的关系，可写出LMS算法的公式如下：因为，所以这种瞬时估计法是无偏的。图9-6 自适应LMS算法信号流图由此可见，自适应LMS算法简单，它既不需要计算输入信号的相关函数，也不要求矩阵可逆。但是，由于LMS算法采用梯度矢量的瞬时估计值，它有较大的方差以致不能获得最优滤波性能。下面从收敛性、学习曲线和失调3个方面分析LMS算法的收敛性能。......
2023-06-23
-
无网格移动最小二乘近似法及其应用详细阅读
Belytschko 等［12］提出基于移动最小二乘近似和Galerkin离散方案的无网格迦辽金法，具有较好的协调性和稳定性，精度和收敛速度高于有限元法，目前已被广泛应用于裂纹扩展、成型加工、渗流问题等不同工程领域。在LS－DYNA 软件中，借助可视判据和快速变换算法［14］，在EFG 法中引入了内聚力模型来模拟裂纹扩展［15］。在LS－DYNA 软件中，EFG 法采用的内聚力模型是初始刚性的线性内聚力模型。......
2023-06-27
-
多目标蚁群算法的设计与优化详细阅读
为消除各类约束导致的大量任务间冲突，获得问题的Pareto解集，本书采用多目标蚁群算法优化任务的调度顺序。由于本章算法为多目标蚁群算法，因此本章算法采取与第3章的优化算法不同的启发策略。本章算法多目标蚁群算法采用自适应策略，在算法起始阶段，启发选择比例参数q 0［式（3-6）］取较大值利于加快收敛速度；在算法搜索后期，选择较小的q 0值可增加种群多样性。......
2023-07-02
-
叶片泵设计简单算法的优化措施详细阅读
它是由SIMPLE算法的提出人之一Patanker完成的。将上述两方面的思想结合起来，就构成了SIMPLER算法。在SIMPLER算法中，经过离散后的连续方程式用于建立一个压力的离散方程，而不像在SIMPLE算法中用来建立压力修正方程。总体而言，SIMPLER的计算效率要高于SIMPLE算法。它也是SIMPLE的改进算法之一，是由Van Doormal和Raithby提出的。......
2023-06-26
-
改进NSGA-Ⅱ的优化算法设计方案详细阅读
MNSGA-Ⅱ具体流程如图9-12所示。MNSGA-Ⅱ以天线资源作为编码依据，在完成对任务的调度预处理之后，将任务所选择的天线资源序号作为种群内染色体基因。图9-13初始种群构造流程2）改进NSGA2算子设计快速非支配排序。......
2023-07-02
-
大学物理实验：最小二乘法的线性回归详细阅读
在一元线性回归中，确定常数A和B，相当于在作图法中求直线的截距和斜率。图0-4密集分布 图0-5分散分布 方程的线性回归，用手工计算是很麻烦的。但是，不少袖珍型函数计算器上均有线性回归的计算键，计算起来极为方便，因此，线性回归的应用日益普及。......
2023-11-02
相关推荐