首页理论教育析出物的生长与熟化方程解析

析出物的生长与熟化方程解析

2023-06-20 理论教育版权反馈

【摘要】：在该附录中，我们可推导出球形析出物的速率。当析出物的直径为纳米尺度时，像在LSW熟化理论中一样考虑曲率的吉布斯-汤姆逊势十分重要。B.1偏析动力学我们先考虑球形颗粒或析出物的生长或溶解过程。因此，B.2.1案例1：析出物的生长通过积分和假设，当t＝0，r＝0时此处需注意，如果我们按照Ham的方法，取Cr为常数，则它不是吉布斯-汤姆逊方程所给出的r的函数。析出物的生长会减少基体中的浓度。

一组析出物的分布函数可通过求解尺寸空间中的连续性方程获得：

式中，f为析出物的尺寸分布函数，ν为析出物的生长/溶解速率。为了求解连续性方程，第一步是得出生长/溶解速率。在该附录中，我们可推导出球形析出物的速率。当析出物的直径为纳米尺度时，像在LSW熟化理论中一样考虑曲率的吉布斯-汤姆逊势十分重要。换言之，界面处析出物/基体处的平衡浓度与半径存在函数关系。当析出物直径大时，我们假设平衡浓度为常数，与半径无关。

B.1　偏析动力学

我们先考虑球形颗粒或析出物的生长或溶解过程。以R为变量，球坐标系下的扩散方程（假设为稳态）为

解为

边界条件为

若取上述两个等式的差值，可得

这是一个很重要的假设。这意味着析出物彼此间距离很远。注意如果我们取体积分数f，即析出物颗粒的体积与扩散区域的体积比或析出相总体积与基体总体积的比则可表示为

这是一个很小的值，f→0。（这是在LSW熟化理论中很重要的一个假设，之后会讨论到。）

故有b＝r（Cr-C0）。将b代入式（B.3）中，可得

同时，有d＝C0，则式（B.1）可转变为

对于半径为r的颗粒而言，在颗粒/基体界面处，或当R＝r时，有

而到达界面处的原子通量为

注意：当Cr>C0，J<0时，净通量是指向析出物颗粒的，因此，析出物会生长。当Cr<C0，J>0时，净通量方向远离析出物颗粒，故析出物颗粒溶解。

B.2　假设Cr为常数时球形颗粒的生长速率

如果Ω是原子体积，在dt时间内，球形颗粒增加的体积为

式中，最后一个式子是由于生长所带来的球壳增量。因此，

B.2.1　案例1：析出物的生长

通过积分和假设，当t＝0，r＝0时

此处需注意，如果我们按照Ham的方法，取Cr为常数，则它不是吉布斯-汤姆逊方程所给出的r的函数。从上述等式可知，。或者可得

B.2.2　案例2：基体中浓度的消耗（考虑平均场）

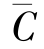另一方面，我们考虑基体中平均浓度由于析出物形成的损耗，，其中基体中平均浓度为 pagenumber_ebook=262,pagenumber_book=248 ，可视为“平均场”浓度（平均场理论中的概念）。开始时，平均浓度为C0，随后由于析出物生长，平均浓度变为¯C。

令1/Ω＝Cp为固态析出物的浓度，则根据质量守恒，可简单得到

式中，

B.2.3　案例3：同时考虑析出物的生长与基体的消耗

我们可通过一种略微不同的方式推导出上述最后一个等式。析出物的生长会减少基体中的浓度。时间Δt内，溶质原子向析出物中扩散的数量为：

它应该等于半径为r0扩散球体积中平均浓度的减少量。因此，如果取基体中平均浓度为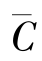 pagenumber_ebook=263,pagenumber_book=249 ，则

或者，我们有

根据质量守恒，则

式中，Cp为固体析出物溶质的浓度，且Cp＝1/Ω。

因此，

把r代入上述速率方程，则有

通过推导，我们可获得

当t＝0，C0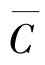＝ pagenumber_ebook=264,pagenumber_book=250 时，β＝0，

因此，我们有溶质

这与我们所获得的公式一致。因此，有

通常，D，Cp，C0已知，因此我们可设计试验来控制析出物的生长。

B.3　吉布斯-汤姆逊势：表面曲率的影响

考虑半径为r的球状物及单位面积γ的表面能。由于球状物趋向于收缩以减小表面能，因此表面能对球体施加一个压力。压力为

如果我们用原子体积Ω乘p，则可得到化学势：

这被称为因表面曲率而得到的吉布斯-汤姆逊势。我们注意到这不只是析出物表面原子的势，而是析出物所有原子的表面能。我们可以看到对于平坦平面而言，r＝∞，μ∞＝0，因此有

接下来，我们将利用这个势来确定曲率对溶解度的影响。当我们考虑合金α＝A（B），其中B为溶剂A中的溶质。在温度T时，B会析出。我们考虑B的两种析出物，其中一种比另一种大，则B在大分子附近的溶解度小于在小分子周围的溶解度。如果我们令X为溶解度，则有

将溶解度与吉布斯-汤姆逊势相联系，则有B化学势关于半径的函数，即

式中，γ为析出物与基体之间的表面能。若定义B的标准状态为纯B，r＝∞，则有

式中，aB为活性。根据亨利定律，则

式中，XB，r为B在半径为r的析出物旁的溶解度。当r＝∞时，

这表明，RTlnaB＝0或aB＝1。因此，k＝1/XB，∞。所以，

因此，

或者，若考虑用kT代替RT，则有

B.4　曲率对溶解性的影响（熟化）

溶质B在半径为r的球形粒子周围的溶解度可由下公式计算得到：

式中，r＝∞时，指数等于1。因此，当r减小时，XB，r增大。现在，我们用Cr取代XB，r，用C∞取代XB，∞，即可得到平面上平衡浓度的表达式，即为

若2γΩ≪rkT，则有

此处应注意C0-C∞>0始终成立。我们可定义临界半径r*为

因此，可得

参数r*可定义为：

r>r*，析出物颗粒在生长。

r<r*，析出物颗粒在溶解。

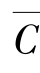r＝r*，析出物颗粒达到一种平衡状态。界面处浓度为 pagenumber_ebook=266,pagenumber_book=252 ，或Cr*＝。

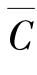在熟化过程中，大粒子的生长是以小粒子的牺牲为代价的。它会达到一个颗粒尺寸的动态平衡分布。这个分布函数可通过在尺寸空间中推导连续性方程得到。得到d r/dt，即是LSW熟化理论的开端。