首页理论教育表面积恒定条件下的非守恒熟化理论

表面积恒定条件下的非守恒熟化理论

2023-06-20 理论教育版权反馈

【摘要】：对于具有一定尺寸分布的笋钉状金属间化合物，令f（t，R）为笋钉状金属间化合物的尺寸分布函数，则笋钉状金属间化合物的总数量为笋钉状金属间化合物的平均尺寸为那么第一个约束条件有如下形式：对于Cu的注入而言，所有沟道的横截面积为生长出的笋钉状金属间化合物的总体积是根据第二个约束条件，可得式中，ni是金属间化合物的原子密度，即单位体积内的原子数；Ci是Cu在金属间化合物中的原子分数，在Cu6 Sn5中Ci值为6/11。

对于具有一定尺寸分布的笋钉状金属间化合物，令f（t，R）为笋钉状金属间化合物的尺寸分布函数，则笋钉状金属间化合物的总数量为

笋钉状金属间化合物的平均尺寸为

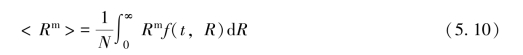
pagenumber_ebook=111,pagenumber_book=97

那么第一个约束条件（即界面面积为常数）有如下形式：

对于Cu的注入而言，所有沟道的横截面积为

生长出的笋钉状金属间化合物的总体积是

根据第二个约束条件，可得

pagenumber_ebook=111,pagenumber_book=97

式中，ni是金属间化合物的原子密度，即单位体积内的原子数；Ci是Cu在金属间化合物中的原子分数，在Cu6 Sn5中Ci值为6/11。流入的Cu原子通量可大约表示为

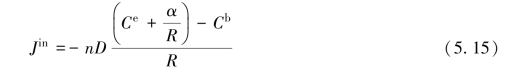
pagenumber_ebook=111,pagenumber_book=97

式中，n是焊料中的原子密度，α＝（2γΩ/kG T）C e，γ是金属间化合物/熔融焊料界面处各向同性的表面张力，Ω是摩尔体积，kG是玻尔兹曼常数，T是温度。C e与C b分别为平整表面上的平衡浓度（熔融焊料中Cu的原子分数）和沟道入口处的平衡浓度（对应基板表面上熔融焊料中Cu的浓度）。

因为笋钉状金属间化合物必须一个原子一个原子地长大或缩小，因此尺寸分布函数在尺寸空间内必须满足连续性方程

pagenumber_ebook=112,pagenumber_book=98

式中，尺寸空间内的速度uR（即半径为R的笋钉状金属间化合物的生长速率）由各个笋钉状金属间化合物上的通量密度j（R）所决定。通常，j（R）的表达式为一个球形晶粒周边无限大空间内的扩散问题的准静态解，该球形晶粒处的过饱和浓度为<C>，而无穷远处浓度为C e。可得

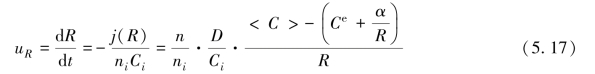
pagenumber_ebook=112,pagenumber_book=98

尽管式（5.17）与LSW理论相符，但是由于笋钉状金属间化合物处于界面处，且它们之间的扩散距离与笋钉状金属间化合物自身尺寸处于同一个数量级，因此它并不适用于当前的例子。另外，由于熔融焊料中原子的扩散速度是非常快的，因此我们建议j（R）的表达式可通过以下方式获得：设反应区域内Cu的平均化学势为μ，假定其处处相同，即近似为平均场；笋钉状金属间化合物与熔融焊料的弯曲界面处的化学势为，其中β＝2γΩ。假设每一个笋钉状金属间化合物流出的原子通量与上述两个化学势之差成正比，则j（R）可表示为

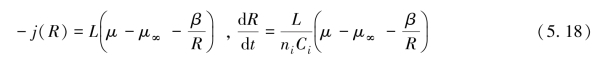
pagenumber_ebook=112,pagenumber_book=98

式中，参数L、β、μ-μ∞可由前述两个约束条件[即表面积恒定约束方程式（5.1）和质量守恒方程式（5.4）]得出。故有

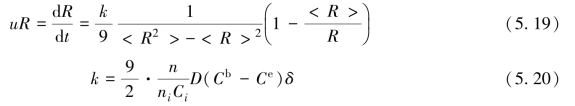
pagenumber_ebook=112,pagenumber_book=98

在通量驱动的非守恒熟化过程中，每个笋钉状金属间化合物生长/缩小的速率不仅由扩散系数和笋钉状金属间化合物的平均尺寸<R>所决定，还与沟道为反应供给Cu原子的能力有关。

因此在近似平均场中，尺寸分布函数的基本方程有如下形式：

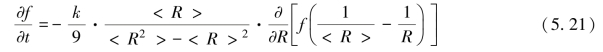
pagenumber_ebook=112,pagenumber_book=98

式中，系数k由流入通量条件决定，而流入通量条件则受控于沟道。

分布函数的正解是

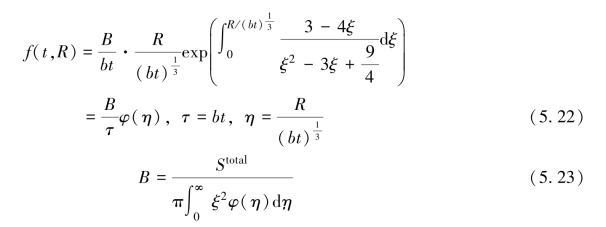
pagenumber_ebook=113,pagenumber_book=99

式中，系数b应通过自洽获得。

通过标准积分运算，可得

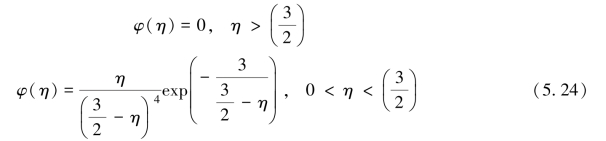
pagenumber_ebook=113,pagenumber_book=99

图5.8所示为φ（η）关于η的函数图像。至此，我们得到了一个可满足通用标量方程（5.15）的特定渐近解。同时，还可得

pagenumber_ebook=113,pagenumber_book=99

式中，参数b＝<η3>

因此，晶粒尺寸立方的平均值为

平均晶粒尺寸为

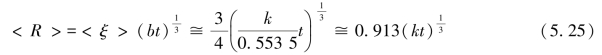
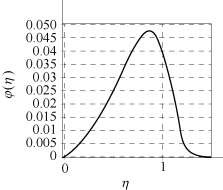
pagenumber_ebook=113,pagenumber_book=99

pagenumber_ebook=113,pagenumber_book=99

图5.8　φ（η）关于η的函数图像

若取n/ni≈1，Ci＝6/11，D≈10-5 cm2/s，δ≈5×10-6 cm，C b-C e≈0.001，其中浓度C b为熔融焊料与Cu3 Sn相处于平衡状态时的浓度，速率常数k≈4×10-13 cm3/s。例如，若退火时间t＝300 s时，则平均晶粒尺寸R≈5×10-4 cm，这一结果与试验结果十分吻合。这说明，熟化速率与晶粒尺寸R的增长由流入的通量条件所决定。