1.伴随矩阵设A是n阶矩阵，则称为A的伴随矩阵，其中，Aij是|A|的元素aij的代数余子式（i，j=1，2，…......
2023-10-27
矩阵运算与分块矩阵简明指南
【摘要】：，n）排成的m行n列的矩形表称为m×n矩阵，aij称为A的第i行第j列的元素（i=1，2，…，As都是方阵），则，|A|=|A1||A2|…，n.于是将式代入式得|A+B|=2n-1，即21-n|A+B|=|A|+|B|.例5.3.3 设n阶矩阵A，B，C满足AB=BC=CA=En，求A2+B2+C2.精解 由AB=BC=CA=En得A2=AEnA=AA==E2n=En，B2=BEnB=BB==E2n=En，C2=CEnC=CC==E2n=En，所以，A2+B2+C2=En+En+En=3En.例5.3.4 设n阶矩阵A，B满足ATA=AAT=En，BTB=BBT=En，且|A|=-|B|，证明：|A+B|=0.精解 由题设知，|A+B|=|EnA+BEn|=|BBTA+BATA|=|B||BT+AT||A|=-|A|2|（A+B）T|=-|A|2|A+B|，即|A+B|=0.由此推出|A+B|=0.
【主要内容】
1.矩阵的概念
由m×n个数aij（i=1，2，…，m；j=1，2，…，n）排成的m行n列的矩形表
称为m×n矩阵，aij称为A的第i行第j列的元素（i=1，2，…，m；j=1，2，…，n）.当m=n时称A为n阶矩阵（或方阵），记它的行列式为|A|.
常见的特殊矩阵有：
（1）零矩阵.所有元素都为零的m×n矩阵称为m×n零矩阵，记为Om×n或O.
（2）单位矩阵.主对角线上元素都为1而其他元素都为零的n阶矩阵，称为n阶单位矩阵，记为En或E.
（3）对角矩阵.除主对角线上元素之外，所有元素都为零的n阶矩阵，称为n阶对角矩阵.
（4）对称矩阵与反对称矩阵.关于主对角线对称的元素彼此相等（或互为相反数）的n阶矩阵称为n阶对称矩阵（或n阶反对称矩阵）.
2.矩阵的加法、数乘与转置运算
（1）加法
设矩阵A=（aij）m×n，B=（bij）m×n，则由A，B产生A+B=（aij+bij）m×n的运算，称为矩阵的加法运算，简称加法.
加法性质：设矩阵A=（aij）m×n，B=（bij）m×n，C=（cij）m×n，则
A+B=B+A，（A+B）+C=A+（B+C），
A+Om×n=A，A+（-A）=Om×n（其中，-A=（-aij）m×n）.
（2）数乘
设矩阵A=（aij）m×n，k为常数，则由A产生kA=（kaij）m×n的运算，称为矩阵的数乘运算，简称数乘.
数乘的性质：设A=（aij）m×n，B=（bij）m×n，k，l是数，则
1·A=A，（k·l）A=k（lA）=l（kA），
k（A+B）=kA+kB，（k+l）A=kA+lA，
|kM|=kn|M|（M是n阶矩阵）.
（3）转置
设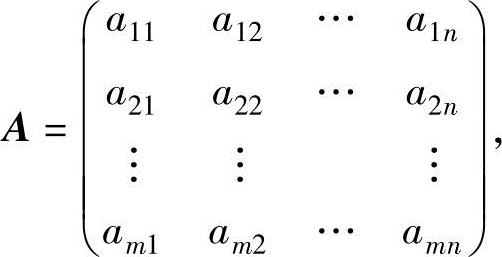
则由A产生
的运算称为矩阵
的转置运算，简称转置，称AT为A的转置矩阵.
设A是n阶矩阵，则A为对称矩阵（反对称矩阵）的充分必要条件是AT=A（AT=-A）.
转置的性质：设A，B都是m×n矩阵，则
（AT）T=A， （A+B）T=AT+BT， （kA）T=kAT，
|MT|=|M|（M是n阶矩阵）.
3.矩阵的乘法运算与乘幂
（1）设矩阵A=（aij）m×l，B=（bij）l×n，则由A，B产生
的运算称为A，B的乘法运算，简称乘法.
乘法的性质：设A，A1是m×l矩阵，B，B1是l×n矩阵，C是n×s矩阵，k是数，则
（AB）C=A（BC），
（A+A1）B=AB+A1B， A（B+B1）=AB+AB1，
（kA）B=A（kB）=k（AB），
（AB）T=BTAT，
|M1M2|=|M1||M2|（M1，M2都是n阶矩阵）.
（2）n阶矩阵的乘幂设A是n阶矩阵，则由A产生
的运算称为矩阵的乘幂运算，称Am(www.chuimin.cn)
是A的m次乘幂，特别地，定义A0=En.
乘幂运算的性质：设A是n阶矩阵，k，l是非负整数，则
Ak·Al=Ak+l， （Ak）l=Akl.
4.分块矩阵
用若干条纵线和横线将矩阵A分成一些小块（小矩阵），以这些小块为“元素”的矩阵称为A的分块矩阵（注意A的分块矩阵与A相等）.
分块矩阵也有矩阵所具有的各种运算，只要把各小块看做元素即可，但需要注意的是各小块（即小矩阵）进行运算时，必须符合运算规则.
常见的分块矩阵运算有：
设
（其中，A1，A2，…，As都是方阵），
则
（k是非负整数），|A|=|A1||A2|…|As|.
设
（其中，A1，A2分别是m1×s1，m1×s2矩阵，A3，A4分别是m2×
s1，m2×s2矩阵）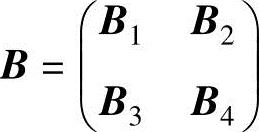
（其中，B1，B3分别是s1×n1，s2×n1矩阵，B2，B4分别是s1×n2，s2×n2矩阵），
则有
【典型例题】
例5.3.1 已知α=（1 2 3），
记A=αTβ，求An.
精解 由于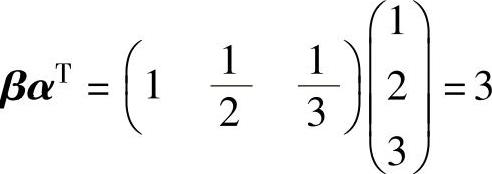
，所以利用矩阵乘法性质计算An.
例5.3.2 已知n阶矩阵A，B只有第j列的对应元素不同，证明：
21-n|A+B|=|A|+|B|.
精解 由题意可设
则
，所以
其中，Aij′是|A+B|的第i行第j列元素的代数余子式，显然，它是|A|的元素aij的代数余子式Aij的2n-1倍，也是|B|的元素bij的代数余子式Bij的2n-1倍，i=1，2，…，n.于是
将式（2）代入式（1）得
|A+B|=2n-1（|A|+|B|），即21-n|A+B|=|A|+|B|.
例5.3.3 设n阶矩阵A，B，C满足AB=BC=CA=En，求A2+B2+C2.
精解 由AB=BC=CA=En得
A2=AEnA=A（BC）A=（AB）（CA）=E2n=En，
B2=BEnB=B（CA）B=（BC）（AB）=E2n=En，
C2=CEnC=C（AB）C=（CA）（BC）=E2n=En，
所以，A2+B2+C2=En+En+En=3En.
例5.3.4 设n阶矩阵A，B满足ATA=AAT=En，BTB=BBT=En，且|A|=-|B|，证明：|A+B|=0.
精解 由题设知，
|A+B|=|EnA+BEn|=|BBTA+BATA|
=|B||BT+AT||A|
=-|A|2|（A+B）T|=-|A|2|A+B|，即（1+|A|2）|A+B|=0.
由此推出|A+B|=0（因为1+|A|2>0）.
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
矩阵初等变换、初等矩阵与等价矩阵解析详细阅读
【主要内容】1.矩阵的初等变换矩阵的下列三种变换称为矩阵的初等行（列）变换：（1）互换矩阵的两行（两列）.（2）用一个非零常数c乘矩阵的某行（某列），即用c乘某行（某列）的每个元素.（3）矩阵某行（某列）的k倍加到另一行（另一列），即某行（某列）的每个元素的k倍，加到另一行（另一列）的对应元素.矩阵的初等行变换与初等列变换，总称矩阵的初等变换.2.初等矩阵单位矩阵经过一次初等变换所得到的矩阵，称为......
2023-10-27
-
高等代数中的分块矩阵及其应用详细阅读
，As都是方阵，那么形如的分块矩阵称为分块对角矩阵，简称分块对角阵，可以简单地记作diag（A1，A2，…，Es）有下面的三种分块初等矩阵：E=diag（E1，…......
2023-11-22
- 详细阅读
-
简易矩阵键盘程序设计指南详细阅读
只要有一列的电平为低，即P3.4～P3.7中有一个“1”，则表示键盘中有键被按下，而且闭合的键位于低电平线与4根行线相交叉的4个按键之中。去除键抖动 为了保证键每闭合一次CPU仅作一次处理，必须去除键释放时的抖动。图20-15 键盘处理程序流程图键盘扫描关键代码如下：......
2023-11-04
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
-
专业能力素质达成矩阵设计与应用详细阅读
课程体系建立后，需要对各门课程的能力素质达成情况进行考查。将课程i的j目标的达成度记为Ti，j，则该课程对专业能力素质培养的总达成度为所有课程对第j项能力素质目标的总达成度为式中，K为开设课程的数量。专业能力素质达成度Q表示为或表示为上述两式具有不同的含义。专业开设的课程和能力素质目标共同构成了专业能力素质达成矩阵，即表3-1所示为其表格形式。......
2023-06-15
-
坐标变换与变换矩阵详细阅读
坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2023-06-19
相关推荐