极限理论与ε-语言详解

2023-10-17 理论教育版权反馈

【摘要】：用“ε-语言”讲述极限概念，可以表述得十分严格。但是，用“ε-语言”定义极限，逻辑结构显得相当复杂。100多年来，“ε-语言”始终占据着微积分的课堂。要真正掌握微积分的原理，就不得不过“ε-语言”这一关。极限的“ε-语言”，既是打开微积分宝库的钥匙，又是阻拦人们获取宝库珍宝的关卡！人们似乎已形成了一种认识：不使用“ε-语言”，就谈不上严格地讲授微积分。

19世纪的数学大师们，是怎样用“极限”概念巩固微积分的逻辑基础的呢？

我们再来回顾一下引起非议的（7.1.1）与（7.1.2）吧。在（7.1.1）中，我们不让h直截了当地等于0。这样，无论它多么小，总有资格当分母。所以，对每个h≠0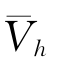， pagenumber_ebook=153,pagenumber_book=141 总是无可非议的。

当h越来越接近0时， pagenumber_ebook=153,pagenumber_book=141 就越来越接近一个数gt。于是，“在h趋于0的过程中，以gt为极限”。用记号表示，就是

这就避开了h＝0的难点。

但这只是极限过程的直观描述，究竟什么叫做“越来越接近”，在数学上是含糊不清的。数学家无法用这种不严格的描述，来进行关于极限的严格逻辑推理。

极限概念的严格定义，应归功于19世纪的法国数学家柯西和德国数学家魏尔斯特拉斯。他们提出了一套极限概念：

函数极限的概念　设函数F（x）在x0附近有定义（在x0这一点可能没有定义），如果存在一个数a，使得对任给的正数ε＞0，总有δ＞0，使0＜｜x－x0｜＜δ时，总有

｜F（x）－a｜＜ε。

我们就说：当x趋于x0时，F（x）趋于a，记作

也就是说，当x趋于x0时F（x）以a为极限。

数列极限的概念　设a1，a2，a3，…，an，…是无穷数列。如果存在一个数a，使得对任给的正数ε＞0，总有N＞0，使n≥N时总有

｜an－a｜＜ε。

就说：当n趋于正无穷时，数列an趋于a，或说数列an以a为极限。记作(www.chuimin.cn)

或

在这些定义中，用到了“ε”这个希腊字母，所以叫做“ε-语言”。用“ε-语言”讲述极限概念，可以表述得十分严格。靠这个小小的“ε-”，就可以说清什么是无穷小，什么是极限。但是，用“ε-语言”定义极限，逻辑结构显得相当复杂。如果把数列极限的概念用数理逻辑的符号表示，就是

① pagenumber_ebook=154,pagenumber_book=142 读作“定义为”；“∃”读作“存在”；“∀”读作“任意的”。

这里包含了四个逻辑层次。这是学生们从小学到高中从来没有遇到过的逻辑结构如此复杂的定义！

100多年来，“ε-语言”始终占据着微积分的课堂。要真正掌握微积分的原理，就不得不过“ε-语言”这一关。但这一关，不仅使一般理工科学生望而生畏，就是数学专业，也把它当做教学上的重点与难点。极限的“ε-语言”，既是打开微积分宝库的钥匙，又是阻拦人们获取宝库珍宝的关卡！美国M.斯皮瓦克在其所编的有名的《微积分》教材中甚至无可奈何地说：“像背一首诗那样把它背下来！这样做，至少比把它说错来得强。”

能不能把极限的基本理论讲得更容易接受一些，更直观通俗一些呢？

科普工作者为此付出过努力，然而当摒弃了“ε-语言”之后，由于追求通俗易懂，往往也就失去了数学的严格性。这样，许多重要的定理就无法证明。没有证明，知其然而不知其所以然，数学几乎就不再是数学了。正如G.波利亚谈到工科学生的微积分教学时所说：“他们没有受过弄懂‘ε-’证明的训练……教给他们的微积分规则就像是从天上掉下来的、硬塞给他们的教条……”

人们似乎已形成了一种认识：不使用“ε-语言”，就谈不上严格地讲授微积分。

实际情形是否真的如此呢？

也许，微积分中的“ε-语言”，会像方块字、十进制、欧几里得的几何体系一样，并非不可代替。

让我们试试看，能不能用更加简单明快的方法，同样严格地讲述无穷小和极限概念。

极限理论与ε-语言详解

相关推荐