施工必备知识点土方施工中，挖湖与堆山也是很重要的工程。挖湖和堆山工程作为土方工程的一个部分，其施工并不是漫无目的地乱挖乱堆，而需要专业人员的测量、定线，依据一定的标准施工，这样才能保证工程的顺利完成。图7-26 极坐标法测设点位2.堆山施工测量堆山施工测量中主要是假山平面位置的测设和各桩点高程的测设。......
2023-08-22
场地平整工程施工测量：园林土方工程施工技术直观解析
【摘要】：场地平整是将需进行施工范围内的自然地面，通过人工或机械挖填平整改造成为设计需要的地面以利现场平面布置和文明施工。在工程总承包施工中，“三通一平”工作通常由施工单位来实施，因此场地平整也成为工程开工前的一项重要内容。
施工必备知识点
在园林工程建设过程中，有时需要对一些园林场地进行平整。场地平整是将原来高低起伏不平的地形，按照设计要求改造为平坦或具有一定坡度的地面，以用于广场、停车场、运动场、苗圃地、草坪用地、建筑用地等。
场地平整是将需进行施工范围内的自然地面，通过人工或机械挖填平整改造成为设计需要的地面以利现场平面布置和文明施工。在工程总承包施工中，“三通一平”工作通常由施工单位来实施，因此场地平整也成为工程开工前的一项重要内容。
实践技能知识点
1.平整成水平地面
（1）布设方格网。方格网法适用于平整地貌起伏不大或地貌变化比较有规律的场地，其首要工作是在待平整的园林场地上布设方格网。方格的边长取决于地形的复杂程度和土石方量要求估算的精度，地面起伏程度越大，布设的方格越小；为了便于计算，方格的边长一般取10m、20m或50m。
如图7-17所示，测设方格网时，通常先在待平整园林场地的边缘选择一点A，安置经纬仪于A点，并沿地块边缘方向确定一条基线Ax；然后从A点开始，按基线方向进行钢卷尺量距，且在地面每隔一定距离钉立一个木桩，依次编号为B、C、D、E。将经纬仪照准部向右水平转动90°得视线Ay，并沿该视线方向每隔一定距离钉一木桩，依次编号为A1、A2。同法，将经纬仪分别安置于B、C、D、E点，并均以Ax为基线，在其垂直方向上每隔20m钉立木桩，得B1、B2、B3、…、E1、E2、E3各点，这样便组成了方格网。
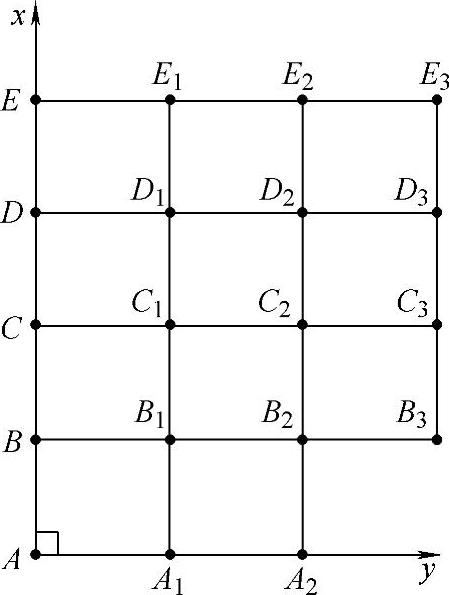
图7-17 布设场地平整方格网
在布设的方格网中，四周只有一个方格的方格点称为角点，如图7-17中的A、E、E3、B3、A2点；四周有两个方格的方格点称为边点，如图中的B、C、D、E1、E2、D3、C3、A1点；四周有三个方格的方格点称为拐点，如图中的B2点；四周有四个方格的方格点称为中点，如图中的D1、D2、C1、C2、B1点。
（2）测量各方格网点的高程。如图7-18示，在待平整场地中的O点安置水准仪，后视已知水准点BM1，前视转点TP1（为防止施工时受到破坏，转点应选在需平整园林场地之外），利用水准测量观测两者之间的高差，计算出TP1点的高程；然后将各方格网点作为“间视点”，分别读取其点位上的水准尺读数（读数至cm即可），并按视线高程法计算出各方格网点的地面高程。
（3）计算设计高程。在园林场地平整中，设计高程虽然可以人为规定，但考虑到整个工程填、挖土方量的平衡，通常用地面平均高程代之，即每一方格的平均高程等于该方格四个方格点的高程相加再除以4，设计高程等于各方格平均高程的算术平均值。
如图7-19所示，方格网上所标注的数据为测量后各方格点的地面高程（为举例计算方便，所标高程数值较小，单位为m），那么，在图7-19中，方格EE1D1D的平均高程为
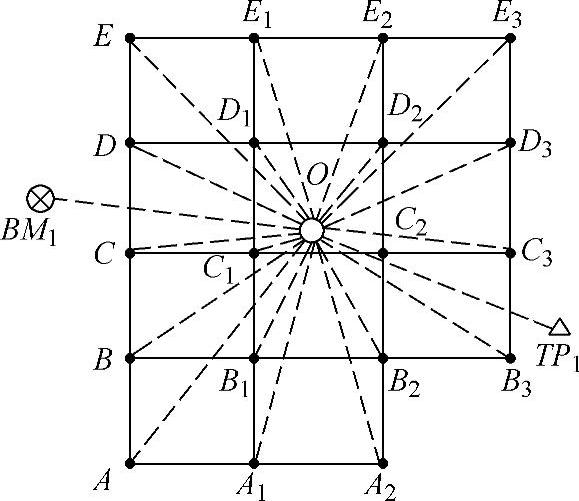
图7-18 测量各方格网点的高程
图7-19 各方格网点的高程值（单位：m）
经分析可知，在设计高程的计算中，角点的高程数据只被采用一次，边点的高程数据被采用两次，拐点的高程数据被采用三次，而中点的高程数据则被采用四次，因此，设计高程计算公式为：
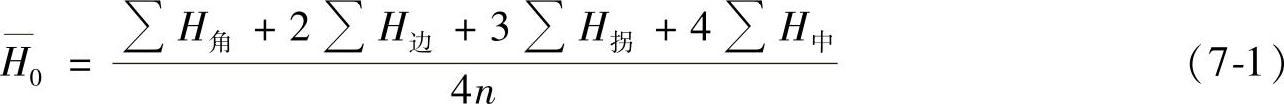
式中 
—设计高程；
∑H角、∑H边、∑H拐、∑H中———分别为各角点、边点、拐点、中点的高程累计之和；n———方格总数。
【例7-1】 根据图7-19中所标注的高程数据，求算平整场地的设计高程。
解：由式（7-1）可得
（4）计算填高或挖深。各方格网点的填高或挖深数量等于设计高程减去该方格点的地面高程，即
h=H设-H地 （7-2）
式中 h———填高或挖深数量，当h>0时表示
填高，当h<0时表示挖深；
H设———平整场地的设计高程；
H地———各方格网点的地面高程。
将平整场地的设计高程、各方格网点的地面高程以及填高或挖深数量标注在一起，可得到图7-20。
图7-20 填高或挖深结果（单位：m）
（5）计算土方量。在园林场地平整中，填、挖土方工程量可按式（7-3）、式（7-4）计算：
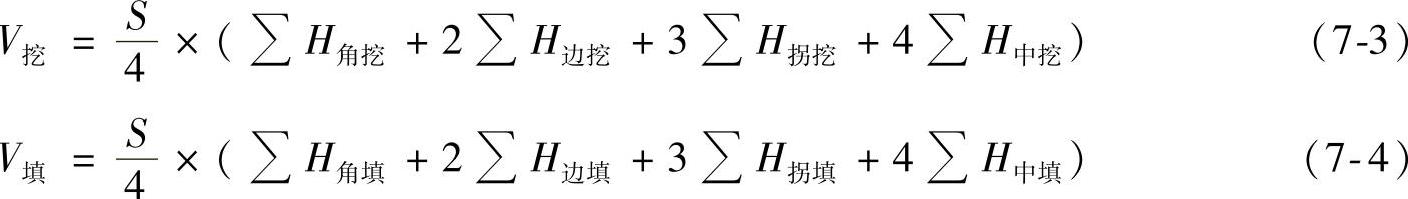
式中 S———方格网中一个方格的面积；
∑H角挖、∑H边挖、∑H拐挖、∑H中挖———分别为各角点、边点、拐点、中点的挖深累计之和；
∑H角填、∑H边填、∑H拐填、∑H中填———分别为各角点、边点、拐点、中点的填高累计之和。
【例7-2】在图7-20中，已知各方格的边长为20m，各方格网点的填高或挖深数据已标注于图中括号内，试求算平整场地中需要填、挖的土方量。
解：由式（7-3）、式（7-4）可得
计算结果表明，填、挖土方工程量基本平衡。（6）决定开挖边界线。在园林场地中，填方区与挖方区的分界线一般在地面高程等于设计高程之处，即填高或挖深为零的位置（零点），将这些填、挖为零的各点连接起来便是开挖边界线如图7-21中的虚线。为便于开挖施工，还应在开挖边界线上撒白灰进行标记。
填高或挖深为零的位置常采用图解法、目估法确定，也可按比例计算求出，其公式为：
式中 x———某一方格边的零点离挖方点的距离；
|h填|、|h挖|———某一方格中，相邻两方格点填高、挖深的绝对值；
a———在方格网中，一个方格的边长。
图7-21 决定开挖线的位置（单位：m）
2.平整成具有坡度的地面
为了节省土方工程和满足场地排水等需要，在填、挖土方平衡的原则下，通常要将图7-19所示园林场地平整成具有坡度的地面。
施工小经验
在平整工作中，坡度大小应视灌溉方式和土质情况而定，横向坡度一般为零，如有坡度以不超过纵坡（水流方向）的一半为宜。另外，为防止水土流失，无论纵坡还是横坡，都不宜超过0.5%。
（1）计算各方格点的设计高程。若将场地平整成具有坡度的地面，首先应选择“零点”，其位置一般选在场地中央的桩点上（如图7-22所示中的C1点）；然后以地面的平均高程作为“零点”的设计高程，并以该点位中心，沿纵、横方向并按照坡降值，逐一计算出各方格点的设计高程。
【例7-3】如图7-22所示，纵向坡降0.2%、横向坡降0.1%，每个方格的边长均为20m；且经计算可知，“零点”C1的设计高程为2.70m，试根据图中所标注的地面高程等数据，求算B1、D1、C、C2点以及其他各方格点的设计高程。
解：由题意，并根据图7-22中所标注的有关数据可得
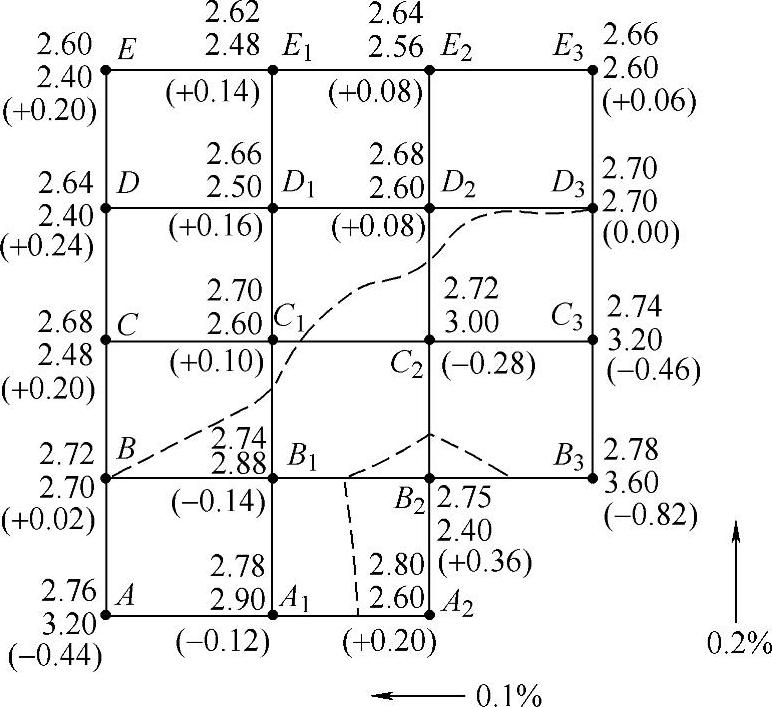
图7-22 平整成具有坡度的地面（单位：m）
纵向每20m长的坡降值为20×0.2%=0.04（m）
横向每20m长的坡降值为20×0.1%=0.02（m）
因此，B1点的设计高程为2.70+0.04=2.74（m）
D1点的设计高程为2.70-0.04=2.66（m）
C点的设计高程为2.70-0.02=2.68（m）
C2点的设计高程为2.70+0.02=2.72（m）
同理，可计算出其他各个方格点的设计高程，一并标注于图7-22中。
（2）计算平均高程。
H0=∑H角+2∑H+3∑H拐角+4∑H中角
- 详细阅读
-
园林工程施工技术+土方工程施工详细阅读
园林中如果没有排水工程，则雨水、污水淤积园内，将会使植物遭受涝灾，滋生大量蚊虫并传播疾病；既影响环境卫生，又会严重影响园里的所有游园活动。因此，在每一个园林工程中都要设置良好的排水工程设施。16）钢桩槽支撑应按“施工小经验”中所述规定施工。......
2023-08-22
-
园林土方工程施工技术，轻松学习！详细阅读
施工必备知识点园林土方回填质量直接影响到路面质量，填筑不好会出现沉降差，发生跳车现象，影响行车速度、舒适与安全，甚至会影响构筑物的稳定，出现交通堵塞现象。图6-33 人工填土图6-34 机械填土......
2023-08-22
-
园林土方工程施工技术挖掘机使用介绍详细阅读
施工必备知识点挖掘机，又称挖掘机械，是用铲斗挖掘高于或低于承机面的物料，并装入运输车辆或卸至堆料场的土方机械。图6-1 挖掘机分类下文主要介绍按铲斗划分的挖掘机。图6-2 正铲挖掘机图6-3 反铲挖掘机图6-4 拉铲挖掘机图6-5 抓铲挖掘机实践技能知识点下面对几种常见的挖掘机作简单介绍。正铲挖掘机的铲土动作形式。反铲式是最常见的挖掘机，向后向下，强制切土。图6-11 轮斗式多斗挖掘机斗轮式多斗挖掘机。......
2023-08-22
-
园林土方工程施工技术的八类土方分析详细阅读
在建设区域，与地形整理和改造相关的设计以及施工过程称为园林土方工程。在土方工程施工中，按土方开挖难易程度将土分为：松软土、普通土、坚土、沙砾坚土、软石、次坚石、坚石、特坚石八类，见表1-1。......
2023-08-22
-
园林土方工程施工技术及平衡调配方法详细阅读
绘制土方调配图，在图中标明调配方向、土方数量及平均运输距离。实践技能知识点1.土方调配土方调配是依据一定的原则和方法进行，为了清晰明了地表明调配情况，可以根据地形设计图绘制一张土方调配图，土方调配图的编制步骤如下。画出土方调配图。将其列于土方平衡与运距表内。在场地土方地形图上，标出调配方向、土方数量及运距。......
2023-08-22
-
园林工程施工技术中的土方量计算详细阅读
土方量的计算是建筑工程施工的一个重要步骤。在现实中的一些工程项目中，因土方量计算的精确性而产生的纠纷也是经常遇到的。所以计算土方量时必须考虑到原有地形的影响，这也是自然山水园土方计算较繁杂的原因。V2、V3、V5～V11计算方法同上。......
2023-08-22
-
园林土方工程施工-快速学习4.1平衡调配原则详细阅读
土方平衡调配工作是土方施工中一项重要内容，它的目的是在土方运输量和土方运输成本最低的条件下，确定填挖区的调配方向和数量，从而达到缩短工期和提高经济效益的目的。经过全面研究、确定业主平衡调配原则后，才可着手进行土方平衡调配工作，例如划分土方调配区、计算土方的平均运距、单位土方的运价、确定最佳的土方调配方案等。......
2023-08-22
相关推荐