【摘要】:若能,请在图中标出来;若不能,请说明理由.3.方程组的解共有_________组.4.已知对任意的有理数a,b,关于x,y的二元一次方程(a-b)x-(a+b)y=a+b有一组公共解,则公共解为_________.5.已知有理数a,b,c,d,e,f满足方程组则f-e+d-c+b-a的值是_________.11.设a1,a2,…
秦九韶,南宋时期著名数学家,《数书九章》是他的代表著作,他对“大衍总数术”(一次同余方程组解法)和“正负开方术”(高次方程的数值解法)的研究,取得卓越的成果.美国科学史家萨顿说:“秦九韶是他那个民族、那个时代,并且确实也是所有时代最伟大的数学家之一.”
知能概述
“消元”是解一次方程组的基本思想,即通过消元把一次方程组转化为一元一次方程来解,而代入法、加减法是消元的两种基本方法.
解未知数系数较大、方程个数较多、含绝对值符号等复杂的方程组时,常用到整体叠加、整体叠乘、设元引参、换元转化等技巧方法,这些技巧方法的运用是建立在对方程组系数特点的观察和对方程组整体特征的把握基础上的.
问题解决
例1 若m使方程组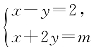 的解x,y的和为6,则m=_________.
的解x,y的和为6,则m=_________.
(湖北省黄冈市竞赛题)
解题思路 用含m的式子分别表示x,y,或运用x+y=6,把原方程组转化为二元一次方程组.
解题——就是意味着把要解的问题化归为已经解决过的问题.
——雅诺夫斯娅
巧测智力
有一次,一位美国心理学家出了这样一道题来测验爱因斯坦的智力:把一个正方形分成16个小正方格,每个小方格分别有苹果、梨、菠萝和香蕉四种水果(如图),小方格的右边和下边分别是4行小方格和4列小方格水果的总重量,要求很快算出左边第一列的水果重量.爱因斯坦很快得出结果,你能解答吗?
例2 若4x-3y-6z=0,x+2y-7z=0(xyz≠0),则代数式 的值等于( ).
的值等于( ).
(全国初中数学竞赛题)
解题思路 视z为常数,解关于x,y的方程组.
例3 解下列方程组:
(1)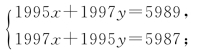
(北京市竞赛题)
(2)
(湖南省湘潭市竞赛题)
(3)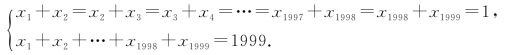
(“华罗庚金杯”少年数学邀请赛试题)
解题思路 对于(1),运用整体叠加法解;对于(2),分别视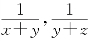 ,
,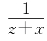 为整体,引入字母简化问题;对于(3),从寻找x1,x3,x5,…,x1997,x1999及x2,x4,x6,…,x1996,x1998彼此间的联系入手.
为整体,引入字母简化问题;对于(3),从寻找x1,x3,x5,…,x1997,x1999及x2,x4,x6,…,x1996,x1998彼此间的联系入手.
所谓“整体叠加”,就是说在解一些复杂的方程组时,若方程组中未知数的系数有规律可循,可直接把方程相加或相减,而不必拘泥于一般意义上的代入法、加减法,就能达到简化方程组的目的.
解数式结构复杂或字母个数过多的问题时,把某一部分看成一个整体或用一个新字母代替,从而达到化繁为简的目的,这就是换元法,恰当地运用换元法,能简化问题结构形式,突出问题的本质特征.
例4 解下列方程组:
(1)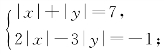
(四川省竞赛题)
(2)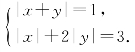
(《数学周报》杯竞赛题)
解题思路 对于(1),解关于|x|,|y|的方程组;对于(2),若逐一讨论,则较繁,利用绝对值如下性质转化问题:当xy≥0时,|x+y|=|x|+|y|;若xy<0时,|x+y|=|x|-|y|或|x+y|=|y|-|x|.
例5 k,b为何值时,方程组
(1)有唯一一组解;(2)无解;(3)有无穷多组解.
解题思路 通过消元,将方程组的解的情况讨论转化为一元一次方程解的情况讨论.
例6 已知关于x,y的二元一次方程(a-1)x+(a+2)y+5-2a=0,当a每取一个值时就有一个方程,而这些方程有一个公共解.你能求出这个公共解,并证明对任何a值它都能使方程成立吗?
(天津市竞赛题)
解法1 令a=1,得3y+3=0,令a=-2,得-3x+9=0.
由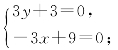 得
得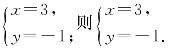 就是所求的公共解.
就是所求的公共解.
将x=3,y=-1代入原方程,得3(a-1)-(a+2)+5-2a=0,
整理得0·a=0.
这表明无论a取什么值,方程总能成立.
解法2 将方程按a整理,得(x+y-2)a=x-2y-5.
因为这个关于a的方程有无穷多个解,
恰当去掉绝对值符号,是解绝对值方程组的关键,常用到绝对值几何意义、绝对值性质、分类讨论等知识方法.
怎样理解并运用条件“当a每取一个值时就有一个方程,而这些方程有一个公共解”?这是解例6的关键.解法1用赋值法,解法2将问题转化为“关于a的一元一次方程解的讨论”.
叠加、叠乘
叠加、叠乘是指解系数有特点的方程组时,不拘泥于一般意义上的代入或加减,而是从整体上把方程组中的几个方程相加(或相减)或相乘,从而达到简化方程组的目的.
例8 能否找到7个整数,使得这7个整数沿圆周排成一圈后,任3个相邻数的和都等于29?如果能,请举一例;如果不能,请简述理由.
(“华杯赛”试题)
解题思路 假设存在7个整数a1,a2,a3,a4,a5,a6,a7排成一圈后满足题意.由此展开推理.若推出矛盾,则原假设不成立.问题的关键是:面对多元、多个等式,怎样处理?
1.已知方程组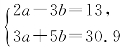 ,的解为
,的解为 则方程组
则方程组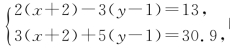 的解是_________.
的解是_________.
(山东省枣庄市中考题)
2.已知关于x,y的方程组 的解是整数,a是正整数,那么a的值为_________.
的解是整数,a是正整数,那么a的值为_________.
(北京市“迎春杯”竞赛题)
条件的不同理解,条件的多重表示,是一题多解的基础.
类似地,请读者思考下面问题:
如图,在六边形的顶点处分别标上数1,2,3,4,5,6,能否使任意三个相邻顶点处的三数之和大于9?大于10?若能,请在图中标出来;若不能,请说明理由.
3.方程组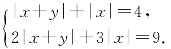 的解共有_________组.
的解共有_________组.
(“五羊杯”竞赛题)
4.已知对任意的有理数a,b,关于x,y的二元一次方程(a-b)x-(a+b)y=a+b有一组公共解,则公共解为_________.
(江苏省竞赛题)
5.已知有理数a,b,c,d,e,f满足方程组
则f-e+d-c+b-a的值是_________.
(“新知杯”上海市竞赛题)
11.设a1,a2,…,a2014是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a2014=69,(a1+1)2+(a2+1)2+…+(a2014+1)2=4001,问a1,a2,…,a2014中有多少个0?
(江苏省扬州市中考题)
12.解下列方程组:
(1)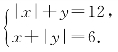
(《数学周报》杯全国竞赛题)
(2)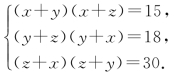
(青少年国际城市数学邀请赛试题)
(3)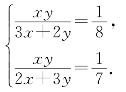
(“五羊杯”竞赛题)
(4)
(青少年数学国际城市邀请赛试题)
13.整体方法
整体思考方法是将问题看成一个整体,从大处着眼,由整体入手,突出对问题的整体结构的分析与改造,从整体上把握问题的特征和解题方向.
阅读材料:善于思考的小军在解方程组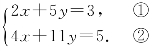 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解 将方程②变形:4x+10y+y=5,即2(2x+5y)+y=5.③
把方程①代入③得:2×3+y=5,∴y=-1.
把y=-1代入①得,x=4.∴方程组的解为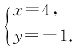
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组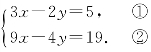
(2)已知x,y满足方程组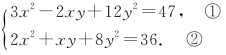
求x2+4y2的值.
(广东省珠海市中考题)
14.试求S=x2003-x2001+x1999-x1997+…+x3-x1的值,其中xi(1≤i≤2003)满足以下方程组:
(澳门校际初中数学竞赛题)
15.已知k是满足1910<k<2010的整数,并且使二元一次方程组 有整数解,问:这样的整数k有多少个?
有整数解,问:这样的整数k有多少个?
(“华罗庚金杯”少年数学邀请赛试题)
16.将若干个自然数按某种规律排列,若前8个数依次是1,3,6,10,15,21,28,36,则第50个数是多少?
(世界数学团体锦标赛试题)
例8 由题意得
a1+a2+a3=29,
a2+a3+a4=29,
……
a6+a7+a1=29,
a7+a1+a2=29.
将上述7式相加,得3(a1+a2+a3+a4+a5+a6+a7)=29×7,
∴a1+a2+a3+a4+a5+a6+a7=67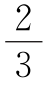 ,与a1+a2+a3+a4+a5+a6+a7为整数,矛盾,故不存在满足题设要求的7个整数.
,与a1+a2+a3+a4+a5+a6+a7为整数,矛盾,故不存在满足题设要求的7个整数.
故共有2个k值使原方程组有整数解.
16.设已知的数依次是a1,a2,a3,a4,…,a50,…,这若干个自然数排列的规律是什么?怎样解多元方程组?
由题意得a2-a1=2,
a3-a2=3,
a4-a3=4,
……
a49-a48=49,
a50-a49=50,
以上49个式子左、右两边分别相加,得
∴a50=1274+1=1275,即其中的第50个数是1275.

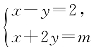 的解x,y的和为6,则m=_________.
的解x,y的和为6,则m=_________.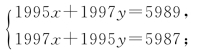

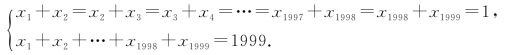
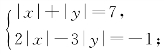
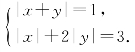

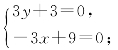 得
得 则方程组
则方程组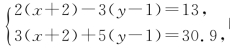 的解是_________.
的解是_________. 的解是整数,a是正整数,那么a的值为_________.
的解是整数,a是正整数,那么a的值为_________.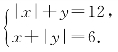
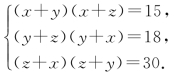
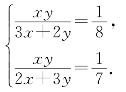

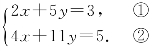 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法: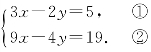
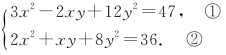
 有整数解,问:这样的整数k有多少个?
有整数解,问:这样的整数k有多少个?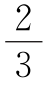 ,与a
,与a






相关推荐