奈氏稳定性判据解析与应用

2023-06-28 理论教育版权反馈

【摘要】：奈奎斯特稳定判据是Nyquist于1932年最先提出的，它是频率法的系统稳定性判据。奈氏判据是根据系统的开环频率特性，来研究闭环系统稳定性的图解判据，同时能确定系统的相对稳定性。例5-7 某单位负反馈系统的开环传递函数为使用奈氏稳定判据分析系统稳定性。

1.奈氏路径

现取如闭合路径Γs，它包围整个s右半平面，s按顺时针方向沿着-j∞→j0→j∞→-j∞绕行，其中从j∞→-j∞是沿半径r→∞的半圆顺时针绕行，如图5-35（a）所示。这个闭合路径称为奈氏路径。

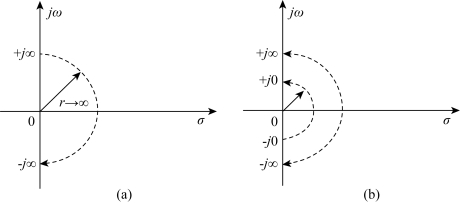
pagenumber_ebook=139,pagenumber_book=128

图5-35　奈氏路径

若Γs之内有F（s）的Z个零点和P个极点，则根据辐角定理，F（s）在Γs内的零点数（即闭环系统的极点数）应为

显然，Z=0时系统稳定。此时，闭环系统稳定的充分必要条件可表述为

如果P=0，则闭环系统稳定的充分必要条件就是N=0；若N≠0，则ΓF包围F（s）平面原点的圈数N就等于系统不稳定的特征根数。

2.奈奎斯特稳定判据

在F（s）平面上与奈氏路径Γs相映射的闭合路径ΓF，即为F（s）曲线。前面的分析是根据F（s）曲线包围F（s）平面原点的圈数N来判别系统不稳定的特征根数Z。由于

WK(s)=F(s)-1

所以，F（s）曲线包围F（s）平面原点的圈数相当于WK（s）曲线包围WK平面（-1，j0）点的圈数。WK（s）曲线即为系统开环幅相频率特性曲线。由此，可得闭环系统稳定的充分必要条件：

WK（jω）曲线（ω自-∞→+∞→-∞）包围WK平面（-1，j0）点的圈数为

对于最小相位系统，P=0，所以闭环系统稳定的充分必要条件是：WK（jω）曲线不包围WK平面（-1，j0）点，即N=0。对于非最小相位系统，闭环系统稳定的充分必要条件是：WK（jω）曲线包围WK平面（-1，j0）点的圈数N=P；如果WK（jω）曲线穿越WK平面（-1，j0）点，则闭环系统就是临界稳定的。这就是奈奎斯特（Nyquist）稳定判据，简称奈氏判据。奈奎斯特稳定判据是Nyquist于1932年最先提出的，它是频率法的系统稳定性判据。奈氏判据是根据系统的开环频率特性，来研究闭环系统稳定性的图解判据，同时能确定系统的相对稳定性。

例5-7 某单位负反馈系统的开环传递函数为

使用奈氏稳定判据分析系统稳定性。

解：系统为非最小相位系统，即

P=1

开环频率特性为

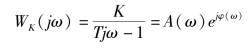
pagenumber_ebook=140,pagenumber_book=129

其中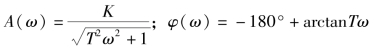， pagenumber_ebook=140,pagenumber_book=129

画幅相频率特性，A（0）=K，φ（0）=-180°；A（∞）=0，φ（∞）=-90°。以K取不同值画开环幅相频率特性曲线如图5-36所示。

当K＞1时，幅相特性如图5-36中的外环，当ω从-∞→+∞时，曲线逆时针包围（-1，j0）点一圈，即N=1，所以Z=P-N=0，闭环稳定；当K=1时，幅相特性如图5-36中的中环，曲线与（-1，j0）点相交，闭环临界稳定；当K＜1时，幅相特性如图5-36中的内环，曲线不包围（-1，j0）点，所以Z=P-N=1，闭环不稳定，在右半平面有一个特征根。

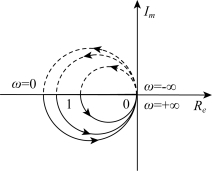
pagenumber_ebook=141,pagenumber_book=130

图5-36　开环幅相频率特性曲线

这一结果，可由闭环特征根的分布情况得以验证。闭环传递函数为

则闭环特征根为，当K＞1时，s＜0；当K=1时，s=0；当K＜1时，s＞0。

3.WK（s）包含有积分环节时的奈氏路径

根据辐角定理，奈氏路径不能通过极点。当WK（s）包含有积分环节时，即在原点有极点，为避开在原点处的极点，s从j0-→j0+的奈氏路径按如图5-37（b）所示以ε→0微小半径的半圆绕过原点极点。

此时s=εejθ。s从j0-→j0+时，则

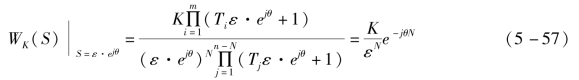
pagenumber_ebook=141,pagenumber_book=130

式（5-58）说明，在s从j0-→j0+、A（ω）→∞时，其相角变化仅由向量s=εejθ决定。从图5-37（b）可见，其相角θ逆时针由-90°→+90°变化了180°，而WK（jω）的相角则顺时针变化180°。若s从j0→j0+变化，WK（jω）的相角则顺时针变化90°。若WK（s）在原点有N个极点，则其相角顺时针变化为N×90°。

由此，开环传递函数含有积分环节的系统的开环幅相频率特性曲线需要补画一段ω从0→0+的增补线，对于最小相位系统，增补线为从正实轴开始、半径为∞、角度为N×-90°的圆弧；对于非最小相位系统，较为复杂，可按式（5-57）的方法讨论。

如图5-37所示为含有积分环节的系统开环幅相频率特性，N为系统型数。

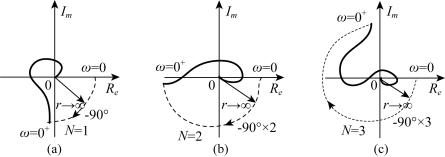
pagenumber_ebook=141,pagenumber_book=130

图5-37　含有积分环节的系统开环幅相频率特性

奈氏稳定性判据解析与应用

相关推荐