第十二部分:孤岛上的父与子挡不住的经济起飞 1 蒋介石是一个独裁者,政治上高高在上,意犹未足,还想身兼各家。 在日本殖民地时代留下的基础上,在美国的大力援助下,加上众多而又廉价勤奋的劳力,使台湾于一九六O年初开始进入经济起飞时期。 第十二部分:孤岛上的父与子挡不住的经济起飞2 蒋氏父子对经建完全外行,他们的贡献应从对经建阻力的大小来衡量。......
2023-11-27
当光伏发电系统作为一种新能源发电装置并入电网,构成分布式发电系统时,就需要考虑孤岛检测和反孤岛控制策略。所谓的孤岛现象,就是指当电网发生故障或维修时,在电网与负载间连接已经断开的情况下,分布式发电系统未能检测出停电状态而没有及时与电网脱离,导致继续给负载供电的情况,从而使分布式发电系统与周围负载形成一个自给供电的孤岛[128]。孤岛现象是分布式发电系统中经常会出现的事故。因而,当光伏并网逆变器直接并网时,除了应具备基本的保护功能之外,还应具备反孤岛效应的特殊功能。从用电安全与电能质量考虑,孤岛效应是不允许出现的。孤岛发生时必须快速、准确地切除并网逆变器。因此,必须对孤岛效应进行检测并加以控制。产生孤岛现象的原因有很多种,但最主要的有以下几种:
1)电网检测到故障,打开断路器,而逆变器并没有检测到故障。
2)设备故障引起系统正常供电中断。
3)配电系统及负载的投切。
4)电网维修时的故意断线。
5)人为的操作失误或自然灾害的作用。
分布式发电系统存在孤岛现象时,会产生如下诸多危害:
1)虽然电力系统已经停电,但本应不带电的线路和负载设备由于分布式发电系统处于孤岛而继续带电,容易会对电力线路维护人员造成伤害。
2)当电力系统不再能控制孤岛状态时,电源的电压和频率可能会对孤岛系统中的用电设备产生一定的损害。
3)当孤岛系统和电力系统电压相位相差很大时,可能引起孤岛系统并网重合闸再次跳闸甚至损坏发电设备和其他已连接设备。
4)当负载需要三相电源供电时,孤岛系统易造成系统三相负载欠相供电。
表5-3给出了专用标准IEEE Std.929—2000[129]和UL1741[130]规定下,并网逆变器在电网断电后检测到孤岛现象并与电网断开的时间限制以及工作频率要求。其中,Unom是指电网电压幅值的正常值;fnom是指电网电压频率的正常值。
表5-3 IEEEStd.929—2000和UL1741对孤岛最大检测时间的限制
另外,我国也对孤岛检测和反孤岛效应方面做出了详细的规定。表5-4列出了我国《光伏系统并网技术要求》(GB/T 19939—2005)中的相关规定[131]:当光伏发电系统并入的电网失压时,必须在2s内将光伏发电系统和电网断开,从而防止孤岛效应的发生。其中,Unom是指电网电压幅值的正常值,对于我国而言,若为单相市电,即为AC220V。fnom是指电网电压频率的正常值,我国的单相市电为50Hz。
表5-4 GB/T19939—2005对孤岛最大检测时间的限制

1.孤岛检测盲区
反孤岛保护是所有并网发电装置所必须具备的功能。然而,几乎所有的反孤岛方案都会存在检测失败的情况,即存在检测盲区(NDZ,Non-Detection Zone)。一般,反孤岛检测失败主要包括功率匹配状况以及一些特殊负载等[132-133]。由于并网逆变器输出侧功率与电网侧功率的差值大小和具体负载可以对NDZ进行定量的描述,而反孤岛方案NDZ的大小反映了该方案检测孤岛效应的有效性,因此,NDZ可以作为性能指标来评估反孤岛方案的有效性。由于不匹配功率的大小可用电网向负载提供的有功功率ΔP和无功功率ΔQ描述,负载可用负载谐振电感L和谐振电容C或负载品质因数Qf和谐振频率fo描述,因此这里定义了以有功功率不匹配ΔP为横坐标、无功功率不匹配ΔQ为纵坐标的功率不匹配坐标系ΔP×ΔQ。
在结合孤岛系统的原理电路以及具体的反孤岛方案进行理论分析时,做出如下假设:
1)并网逆变器运行于单位功率因数的控制模式,即Q=0,ΔQ=QL。
2)并网逆变器近似为电流源。
3)负载为电阻R、电感L和电容C的并联。
4)电网电压和频率恒定。
2.无源(被动式)检测方法
(1)过/欠电压、过/欠频保护的检测盲区
图5-30描述的孤岛系统原理图由并网逆变器、RLC并联负载、网侧变压器以及电网组成。其中,电网一方面提供负载所需的无功功率,另一方面当并网逆变器输出的有功功率小于负载所需的有功功率时,向负载提供相应的有功功率,而当并网逆变器输出的有功功率大于负载所需的有功功率时,吸收多余的有功功率。当电网跳闸而出现孤岛现象时,本地负载完全由逆变器单独供电。因此,负载电压的幅值、相位或频率会发生相应的变化,无源检测就是通过检测负载电压的变化来判断孤岛的发生与否。

图5-30 孤岛系统原理图
当孤岛系统中采用图5-30所示的RLC并联电路来模拟本地负载时,负载上消耗的功率为

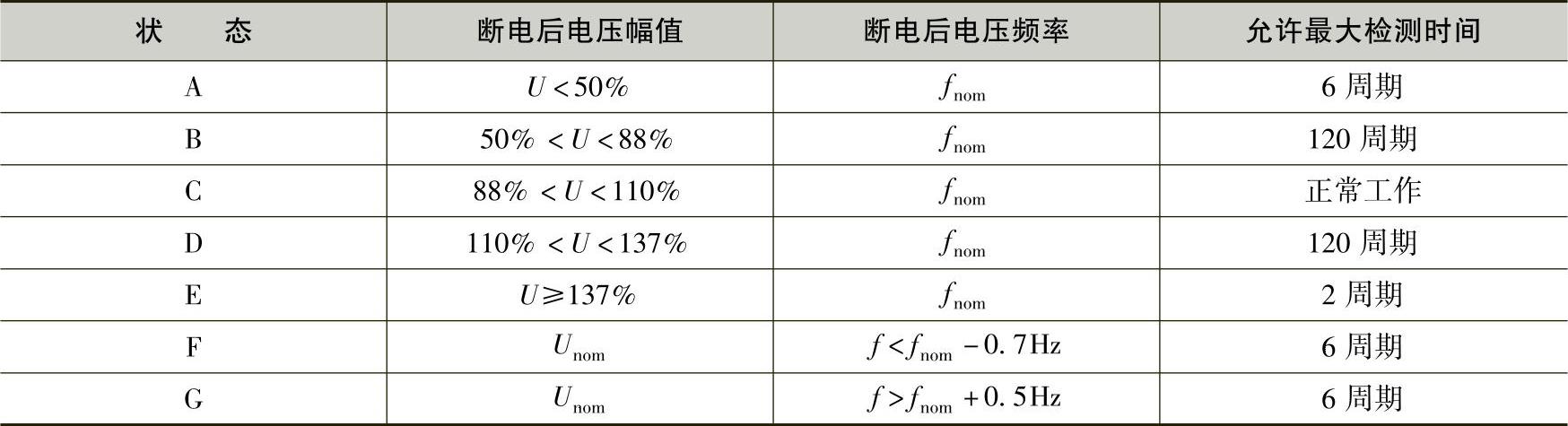
式中,Ua为并网逆变器与电网的公共连接点a的电压幅值;ω为电压Ua的频率。
当逆变器并网运行时,电网向负载提供的部分功率为ΔP和ΔQ。当电网因为故障而跳闸(即k断开)时,并网逆变器开始独立向负载供电。此时ΔP=ΔQ=0。因此,独立供电系统的运行状况取决于断路器k断开前的ΔP和ΔQ,并存在OVP(过电压保护)、UVP(欠电压保护)、OFP(过频保护)和UFP(欠频保护)四种情况。
1)ΔP<0时,并网逆变器输出的功率大于负载消耗的有功功率,即P>PL。当断路器k断开的瞬间,ΔP突降为零。因此,PL会增大为P。而R在短时间内不会发生明显的变化,由式(5-22)可知,Ua将增大。如果a点电压超出OVP设定的阈值,即可检测到孤岛现象的发生。
2)ΔP>0时,并网逆变器输出的功率小于负载消耗的有功功率,即P<PL。当断路器k断开的瞬间,ΔP突降为零。因此,PL会减少为P。而R在短时间内不会发生明显的变化,由式(5-22)可知,Ua将减少。如果a点电压超出UVP设定的阈值,即可检测到孤岛现象的发生。
3)ΔQ>0时,负载需要吸收无功功率,是滞后功率因数角,即负载在电网频率下呈感性。当k断开时,ΔQ=0,由于逆变器以单位功率因数供电,即Q=0。因此,负载无功功率QL会减少到零。由式(5-23)可知,公共连接点电压Ua的频率会增加到负载固有谐振频率ωs。如果Ua的频率超出了OFP设定的阈值,即可检测到孤岛现象的发生。
4)ΔQ<0时,负载将产生无功功率,是超前功率因数角,即负载在电网频率下呈容性。当k断开时,ΔQ=0,由于逆变器以单位功率因数供电,即Q=0。因此,负载无功功率QL会变为零。由式(5-23)可知,公共连接点电压Ua的频率会减少到负载固有谐振频率ωs。如果Ua的频率超出了UFP设定的阈值,即可检测到孤岛现象的发生。
并网发电系统采用OVP、UVP、OFP和UFP时,在逆变器输出功率与负载需要的有功功率或者无功功率不匹配的情况下,一旦出现孤岛运行状态,公共连接点电压的幅值或者频率会发生变化。如果超出预设的阈值就可以判断出孤岛的发生,从而采取相应的保护措施。然而,当逆变器输出功率与负载需要的有功功率或者无功功率基本匹配时,公共连接点电压的幅值或者频率变化较小,则该方法就会失效,就不能检测到孤岛现象的发生。
(2)电压相位突变检测法(PJD)
逆变器并网运行时,公共连接点a的电压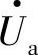 由电网电压
由电网电压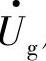 所钳位,即有
所钳位,即有

式中,Um为电网电压幅值;φ0为电网电压初始相位。
逆变系统并网发电运行时,应使逆变器输出电流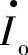 与电网电压同相位,以实现功率因数并网发电,即
与电网电压同相位,以实现功率因数并网发电,即

式中,Im为并网逆变器额定输出电流幅值。
此时,负载电流由a点电压决定,即由电网电压决定,因此有
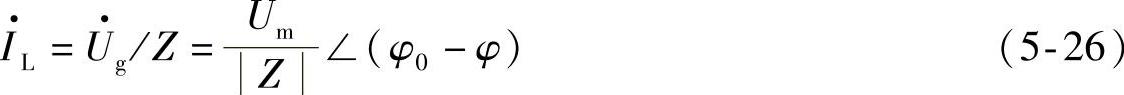
由上式可见,并网运行时负载电流与电网电压的相位差由负载阻抗角φ决定。当电网突然断开后(即断路器k断开),出现了逆变器单独给负载供电的孤岛现象。在孤岛现象发生前,逆变器输出电流Io与电网电压Ug仅在过零点发生同步。在过零点之前,Io要跟随系统内部的参考电流而不发生突变。因此,孤岛现象发生后负载电流会突变为逆变系统的输出电流,即

此时,a点电压由逆变器输出电流Io和负载阻抗Z所决定,即有

由式(5-28)和式(5-24)对比可见,孤岛现象发生后,a点电压的相位将会发生变化。因此,可以采用电压相位突变检测方法来判断孤岛现象是否发生。如果负载为非纯阻性负载,则负载阻抗角φ使输出电压Ua发生相位突变。例如,通过检测a点电压Ua与逆变系统输出电流Io之间的相位差φ,如果φ大于系统所规定的阈值,说明孤岛现象发生,控制器将断开或关闭并网逆变系统。
相位突变检测算法简单、易于实现,属于无源检测方法,不会影响逆变系统输出电能的质量,也不会影响系统的暂态响应。相位突变检测与过频、欠频检测相类似。在电网频率下,当负载阻抗角φ接近零时,即负载近似呈阻性时,该方法失效。通常相位突变检测需要与过电压、欠电压检测结合应用,以减少检测盲区,提高孤岛效应检测的可靠性。
(3)电压谐波检测法
电压谐波检测法是指通过监测公共连接点电压Ua的总谐波畸变率(THD)的变化来判断THD是否超出设定的阈值范围,从而来检测孤岛现象是否发生。在图5-30中,公共连接点电压Ua的谐波主要来自如下两个方面:一是来自电网,由电网电压畸变导致Ua产生电压畸变;二是由于高频开关逆变器产生的电流谐波而引起Ua电压产生畸变。通常情况下,电网电压的谐波畸变比较小且基本恒定。当并网逆变器与电网并网运行时,逆变器产生的电流谐波将通过公共连接点a流入电网。由于电网的阻抗很小,因而a点电压的THD通常较低。而当电网断开后,并网逆变系统所输出的电流谐波将流入负载,由于本地负载阻抗通常要比电网阻抗大得多,因而逆变器的输出电流谐波将在a点产生较大的谐波电压。根据前述原理可看出,通过检测公共连接点的电压Ua的谐波含量,并与设定的阈值比较,若Ua的THD超出所设定的阈值范围,则说明逆变系统处于孤岛状态,应提供相应的保护。理论上,电压谐波检测方法在一定范围内提高了孤岛现象的检测可靠性。但在实际应用中,由于本地负载的非线性因素、并网逆变器的输出THD指标限定(一般要求THD<5%)以及电网电压本身若存在较大的谐波等情况,将使该检测方法下的阈值比较难以确定。因此,该方法存在较大的局限性。
3.有源(主动式)检测方法
有源孤岛现象检测通常是通过给系统注入一定的扰动信号后,系统在孤岛现象发生时使公共连接点电压Ua产生明显的变化。有源孤岛检测主要包括有源电流扰动和有源频率偏移(Active Frequency Drifting,AFD)等方法。有源孤岛现象检测方法中,引入的扰动能够破坏并网逆变器输出和负载之间的功率平衡,进而检测到孤岛现象的发生,有效地减少检测盲区。
(1)有源电流扰动法
有源电流扰动法是通过给并网逆变器施加周期性的电流扰动,以破坏逆变器与负载之间的功率平衡,从而达到检测孤岛现象的目的。在孤岛现象发生后,通过检测公共连接点的电压变化,从而判断出孤岛现象的发生。有源电流扰动法通常需要与过电压、欠电压检测结合使用。在单独采用过电压、欠电压检测时,如果逆变器额定输出功率与本地负载功率相匹配,在逆变器脱网运行时,公共连接点的电压不会发生明显的变化。此时,过电压、欠电压检测失效。这时,如果改变逆变器输出电流的幅值,则公共连接点电压的幅值就会发生相应的变化。当超出设定的阈值时,可以判断出孤岛的发生。如果逆变器并网运行,公共连接点的电压由电网电压所钳位,即使引入电流扰动也不会改变连接点的电压。
有源电流扰动检测方法具有原理简单、容易实现、电流谐波小等特点。但是,并网电流周期性变化,对逆变系统输出功率影响较大,对系统的动态性能要求较高。在多台逆变系统并网运行时,单台逆变器的电流扰动对公共连接点电压的影响减弱,降低了孤岛现象检测的可靠性。
(2)有源频率扰动法
有源频率扰动法(AFD)是通过对并网电流的频率施加扰动,使系统工作频率逐步偏移,从而来检测孤岛现象的方法,如图5-31所示。并网运行时,每个周期逆变器输出电流的初始相位都跟踪电网电压的相位,因此,微小的电流偏移对系统的正常运行不会产生明显的影响。当孤岛现象发生时,公共连接点电压Ua的频率会由于电流的偏移而发生改变,并产生一定的正反馈,从而加大Ua的频率偏移。当频率超出预设的阈值时,可以检测到孤岛现象的发生。
应用有源频率扰动法检测孤岛现象时,在阻性负载情况下,当电网跳闸时,在正半周期公共连接点的电压波形会跟随逆变器输出电流波形,在Tu/2-tz后变为零,使连接点电压Ua比电网电压提前tz达到零;到负半周期,逆变器电流又会提前tz过零,从而使Ua的频率进一步增加,当超出预设的频率阈值时,可以检测到孤岛的发生。当频率扰动检测法应用于感性负载时,由于感性负载上的电压超前于电流,因而在断网后有使连接点电压的频率上升的趋势,使其更快地超出频率保护阈值,从而检测出孤岛的发生。但是该方法应用于容性负载时,由于容性负载上的电压滞后于电流,因而在断网后有使连接点电压频率下降的趋势,如果频率下降的趋势和逆变器输出电流产生频率上升的趋势相抵消,则这种检测方法会失效。
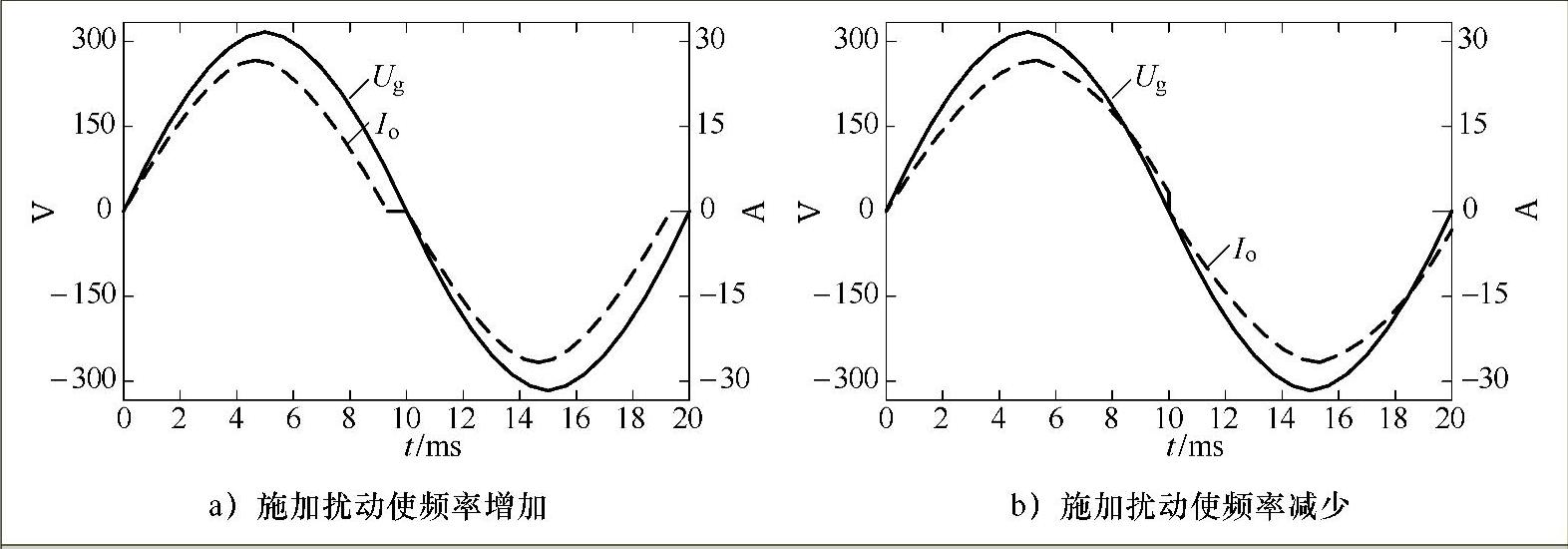
图5-31 频率扰动法原理示意图
图5-32所示为孤岛现象发生时的波形示意图。其中,ug为公共连接点电压(也是图5-30中的本地负载电压);io为逆变器输出电流,即负载电流;Tu为交流电压周期;Ti为电流给定周期。以负载电压对电流基波的响应分析频率扰动下的相位关系,if为io的基波分量。由图所示可以得出,工作频率与频率扰动方向和幅度的关系。图5-32a所示是施加扰动使频率变大,Ti<Tu,负载阻抗角小于零,电压滞后于电流;图5-32b是施加扰动使频率变小,Ti>Tu,负载阻抗角大于零,电压超前于电流。由图可以看出,所测出的电压周期Tu(孤岛下系统频率f即电流基波频率的倒数)与实际电流给定周期Ti不相等,所施加频率扰动无法反映到频率(周期)检测中,即所检测到的输出端电压的频率并非给定电流的实际频率,负载阻抗角抵消了频率扰动作用,无法使频率进一步偏移,从而有
φL+φAFD=0 (5-29)
式中,φL为负载阻抗角,φAFD为电流扰动带来的相位扰动。
对于图5-32a所示的正向频率扰动,负载电压ug滞后于电流io的基波if,滞后相差为φL,电压、电流间的相位差与负载阻抗角间的关系为

由上式可得到负载阻抗角φL
φL=0.5π(Ti-Tu)/Tu(5-31)系统工作频率为f=1/Tu,电流给定频率fi=1/Ti,频率扰动量

从而有

同理,由图5-32b也可得到上式所示的相位关系,式(5-29)和(5-33)是孤岛情况下的负载特性与AFD频率扰动方法(扰动方向与幅度)的相角关系。
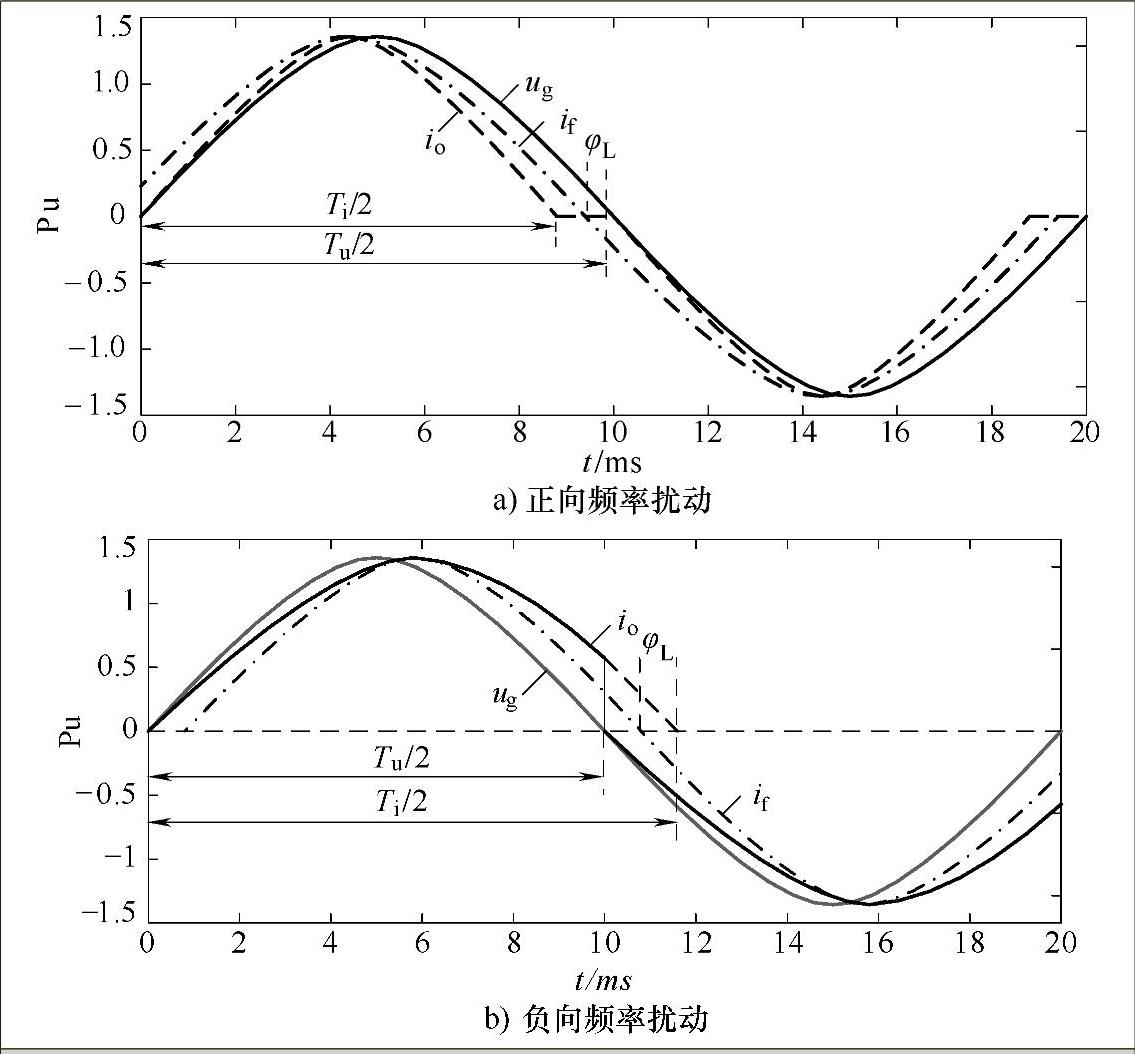
图5-32 频率扰动下负载电压和电流波形示意图
在不考虑电流闭环相位跟踪误差的基础上,施加扰动使频率变大。
有关电力电子技术在电力系统中的应用的文章

第十二部分:孤岛上的父与子挡不住的经济起飞 1 蒋介石是一个独裁者,政治上高高在上,意犹未足,还想身兼各家。 在日本殖民地时代留下的基础上,在美国的大力援助下,加上众多而又廉价勤奋的劳力,使台湾于一九六O年初开始进入经济起飞时期。 第十二部分:孤岛上的父与子挡不住的经济起飞2 蒋氏父子对经建完全外行,他们的贡献应从对经建阻力的大小来衡量。......
2023-11-27

第十二部分:孤岛上的父与子思想冰河文化沙漠 1 一九五九年,三位美国学者在台湾实地调查教育文化状况,写了一篇报告,直指台湾是“文化沙漠”?“各种禁忌”,乃是政治高压的产物;在政治高压下,思想不仅受到限制,根本受到禁锢,以至于形成冰河状态。然而在蒋氏父子的高压下,思想有问题是可以被枪毙的,有几个人敢惹“思想”,当然导致思想的冰河,而文化沙漠正是思想冰河之果。经人检举,判刑十五年。......
2023-11-27

第十二部分:孤岛上的父与子亡命又亡国 1 蒋介石下野原是情非得已,在国内,徐蚌惨败,精锐尽失,权力基础大受冲击;在国外,美国总统杜鲁门态度冷淡,宋美龄出访,毫无成就。 四月二十五日的一别,竟是蒋氏父子永别故里。 第十二部分:孤岛上的父与子亡命又亡国2 一九四九年十月一日,毛泽东宣布成立中华人民共和国,同月十二日共军已临广州市郊,“国民政府”再迁重庆。......
2023-11-27

因而有文献指出,可进行人工干预,根据不同的季节来改变CVT控制的基准,从而实现MPPT控制。所以说,CVT控制无法实现真正意义上的MPPT控制,具有较大的弊端和局限性。下面结合图5-20和图5-21来描述扰动观测法的MPPT过程。......
2023-06-23

“自杀爆炸者就是这样渗透到以色列的?”安还说,吉普车驶过的许多道路正是近几年形成的,因为原来的道路已经被以色列封死。隔离墙打破了巴勒斯坦人与土地之间的联系,失去土地的巴勒斯坦人将变成以色列或邻近阿拉伯国家的工厂奴隶,安这样形容。......
2023-11-01

本节利用两个轴的坐标系,生成坐标定义铰。进入模型运动模拟工作台操作参见1.3。生成坐标系定义铰单击工具栏内的图标,要单击这个图标,需要先单击图标右下方的箭头,出现所有铰定义图标。单击图标后,出现对话框,如图13-3所示。对话框内的和栏内显示所选择的坐标系。本章在零件设计中也有新内容,局部坐标系的定义以前未讲过。......
2023-07-01

第十二部分:孤岛上的父与子屈辱的对日和约1 一九八七年十一日三十日,日本政府公布了《中日和约》的外交档案。而所谓其他条件,则是“与旧金山和约规定的联合国会员国同等地位”及承认国府为全中国的代表等。蒋介石脸上无光,只好等日本单独和他签约。 第十二部分:孤岛上的父与子屈辱的对日和约2 本人日来夜不成寐,阅读史料,至李合肥?......
2023-11-27

在此基础上,基于此功能架构我们提出了一种实现多层资源优化跨无线、光和BBU层的全局评价方案,以保证QoS的要求。在第一阶段,GES可以根据全局评估因素在多层资源中选择最佳的目的地BBU。为了衡量业务供应选择的合理性,我们定义α作为考虑所有多层参数的全局评估因子。在BBU函数中,由于维度不同,很难对CPU和存储的利用率进行评估,为了测量BBU选择处理的合理性,可调整比例权重φ来调整其比例。......
2023-06-19
相关推荐