国际标准建议CCITT H.261、JPEG、MPEG中都采用8×8的块做DCT,但基于DCT的数字滤波尚不普遍。为使DCT所具有的优良特性能在数字滤波中得到充分发挥,结合全相滤波的概念提出了DCT域ap系统设计。TN-2TN-1],其传输特性为显然,apDCT具有严格零相位。实现无窗、单窗和双窗apDCT与传统滤波器特性的MATLAB代码如下:显然,apDCT具有严格零相位。利用apDCT的各子带滤波器对图像的一行进行子带滤波的结果如图4-8所示。......
2023-06-23
近年来,由于数字技术、计算机技术以及DSP技术的迅速发展和广泛应用,迫使人们寻求更适用于这些新技术的分析工具,发现了还有很多其他函数在一定意义下比三角函数或指数函数更为优越,沃尔什(Walsh)函数就是其中之一。沃尔什函数系是一种完备正交函数系,每个函数只能取+1与-1两个值,就是所谓的二值正交函数。它的特点是图形呈矩形,有跳变特性,在跳变点间仅取上述两个数值,这与数字逻辑电路中的两个状态相对应,同时满足了完备和正交特性,从而可以进行级数展开与函数变换。因此,以沃尔什函数为基础所构成的变换,是实数加减运算,比傅里叶变换速度快。通常把沃尔什变换这类解析方法称为序域法,把基于这种变换法实现数字滤波的系统称为序率滤波器,又叫做列率滤波器。基于沃尔什变换的ap(简记为apDWT)是对经加窗处理后的输入信号作离散沃尔什变换,对得到的沃尔什域信号加权处理后再经过IDWT,并再次加窗处理,移位相加输出。系统原理同图2-26所示,对应的输出为
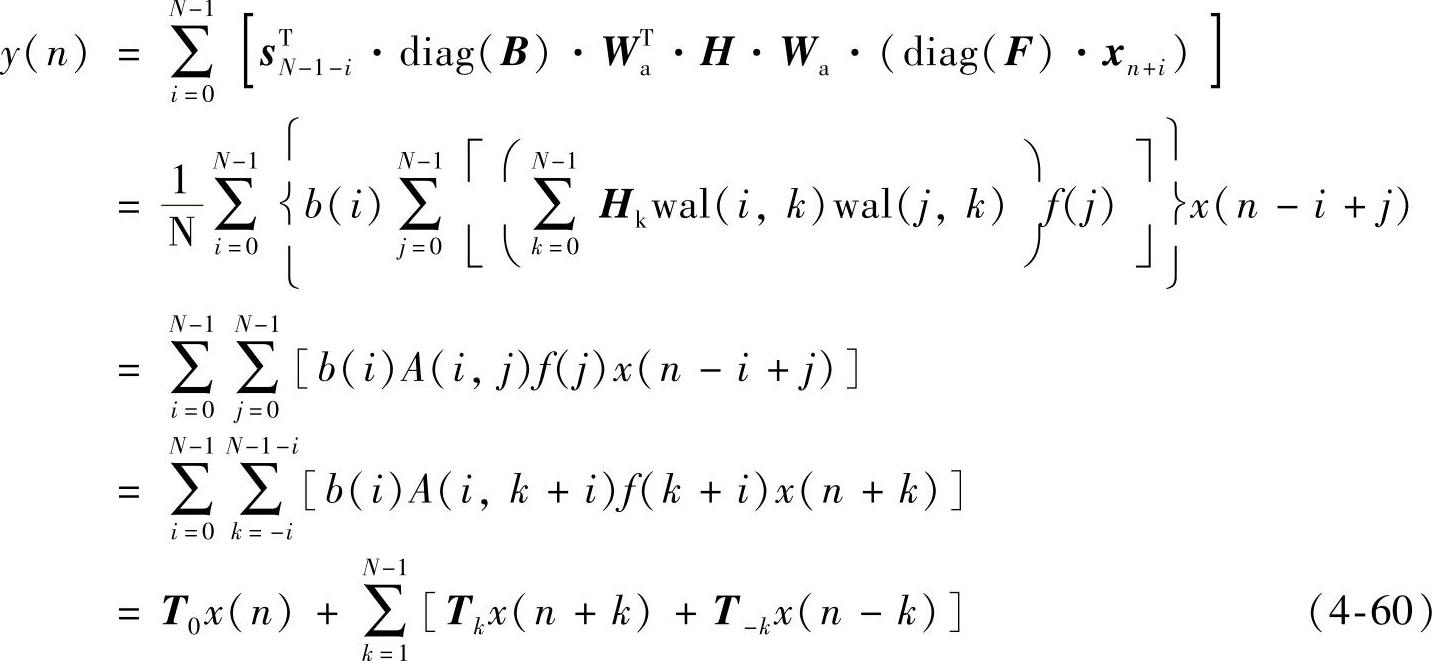
式中
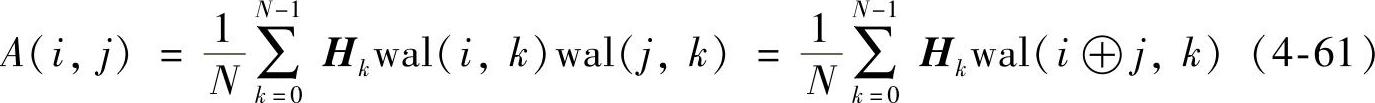
Tk的表达式与apDCT时相同。结合沃尔什变换的性质,易证明矩阵A仍具有式(4-52)表示的主对称性和式(4-53)表示的次对称性。此外,apDWT具有与apDCT相同的传输特性函数形式,因此也具有严格零相位的特性。沃尔什变换基具有正交基的一般性质,所以对于互补的系统特性H1和H2,对应的单位冲击响应序列T1和T2仍具有式(4-58)的结论。
参照函数apDCT容易写出apDWT(不再列出),生成的特性曲线如图4-9所示。
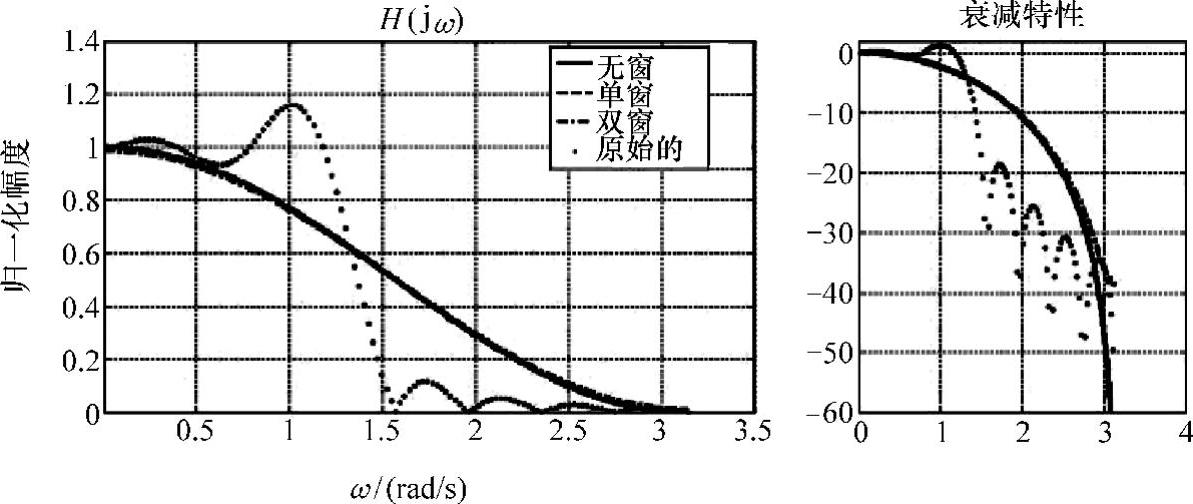
图4-9 apDWT与传统法特性曲线
与apDCT相同情形下,按照2倍频子带分解求得各apDWT子系统冲击相应如下:

各子带的传输特性如图4-10所示。利用它对图像的一行进行子带滤波的结果如图4-11所示。

图4-10 apDWT各子带传输特性
signal为原始信号,H0~H4分别为三个带通子带信号,H0为低通子带信号,H4为高通信号。由图中可以看出,四个子带均无方块化痕迹。沃尔什变换具有某种能量集中性,原始数据分布越均匀,则变换后的数据越集中在矩阵边角上,因此在数据压缩方面比较实用。
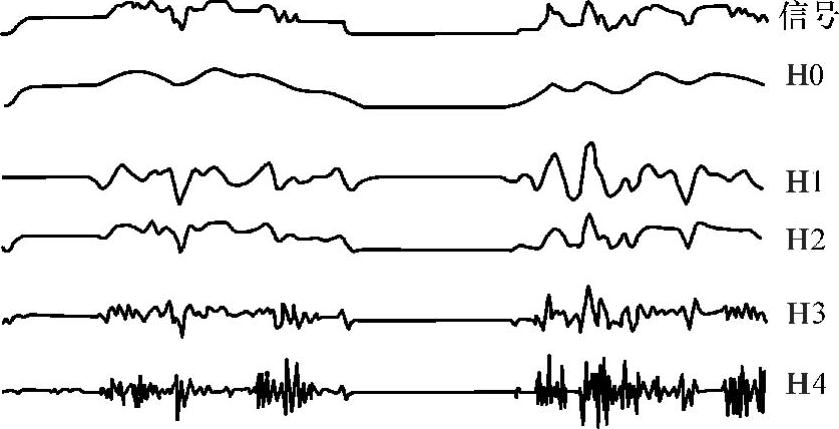
图4-11 基于apDWT子带分解信号图
实际上,不论是何种正交变换,按照全相位信号处理方法得到的ap都可以对信号进行去除分段效应的滤波和处理,它是建立在新概念上的一种滤波系统。而由此带来对传统信号处理方法的改变则超出了它本身的定义,如自适应滤波、谱分析等都会得到良好的效果。
有关全相位数字信号处理方法及MATLAB实现的文章

国际标准建议CCITT H.261、JPEG、MPEG中都采用8×8的块做DCT,但基于DCT的数字滤波尚不普遍。为使DCT所具有的优良特性能在数字滤波中得到充分发挥,结合全相滤波的概念提出了DCT域ap系统设计。TN-2TN-1],其传输特性为显然,apDCT具有严格零相位。实现无窗、单窗和双窗apDCT与传统滤波器特性的MATLAB代码如下:显然,apDCT具有严格零相位。利用apDCT的各子带滤波器对图像的一行进行子带滤波的结果如图4-8所示。......
2023-06-23

即N阶频域全相位滤波器与2N-1阶加三角窗的FIR滤波器等效,此FIR滤波器的单位冲击响应是全相位滤波器特性H的反离散傅里叶变换的两个周期延拓,第一等效图如图2-17所示。图2-17 N阶无窗全相位滤波器第一等效图以下MATLAB代码验证了图2-17与图2-15的DFT域全相位等效。......
2023-06-23

为进一步改善系统性能,充分发挥窗函数在滤波器设计中的作用,综合上面两种情形得到在DFT前和IDFT后均加窗的全相位数字滤波器结构如图2-26所示。图2-28 加双窗对比单窗滤波结果对比上面介绍的3种带窗全相位数字滤波器具有完全相同的FIR滤波器等价结构,区别仅仅在于卷积窗的生成方法。为了便于讨论,将第1种类型称无窗全相位数字滤波器,第2种和第3种类型称单窗全相位数字滤波器,第4种类型称双窗全相位数字滤波器。......
2023-06-23

20世纪70年代初,滤波器组首先在语音编码和多路复用中得到了应用。所谓滤波器组就是将信号按不同的频带分解成一组信号,并将分解得到的子带信号重新合成原信号的处理系统。80年代后期,M.J.Smith等人提出了运用谱分解法设计无失真地重建原始信号的滤波器方法,但存在相位失真。......
2023-06-23

图2-22 加前单窗的全相位数字滤波器记前窗序列为F=[f(N-1)…因此,对比无窗全相位数字滤波器的唯一区别就是卷积窗的大小和形状。从图中可看出,单窗全相位数字滤波器极大地改善了通带及阻带内的波纹数量且降低了波纹幅度,最小旁瓣衰减也降低了6.8dB。图2-23 加前单窗对比无窗全相位数字滤波器特性在MATLAB代码中可以设置不同的窗函数来调整滤波器特性,设置不同的H来对信号进行滤波。......
2023-06-23

图4-12 变换域信号处理图对于N阶系统,时刻n输入xn=[x,x(n-1),…其中X1是1维N阶全相位输入信号,即式就是全相位数字信号处理得到的输出与输入的数学关系表达。把式称为全相位变换,矩阵A称为全相位变换基,矩阵T则为全相位变换核。综合以上,变换域全相位数字信号处理一种可能实现如图4-16所示。......
2023-06-23

对于ap2 DCT的全相位变换核,有式中符号表示异或运算。基于此结论的ap2 DCT和ap2 DWT的全相位变换基也具有对称性。以图5-20给出的3种卷基窗分别形成的二维apDCT传输特性如图5-21所示。图5-21 ap2nsd DCT特性曲面及曲线图从图中可看出apDCT的平滑性好于apDFT,ap2d DCT的衰减特性比ap2n DCT低20dB,但由于采用与ap2n DCT和ap2s DCT相同的归一化条件,峰值幅度低于1且过渡带宽度增大。......
2023-06-23

长度为N的单边带H0按上面3种方法设计生成的ap半带滤波器H的长度为2N-1。在满足条件1、2、3下,ap1 nsd半带滤波器H、单边带H0和卷积窗C的零点分布如图7-22所示。ap1ns半带滤波器的H零点由单位圆上和内及对应的倒数组成,而ap1 d半带滤波器的H零点只由单位圆内及对应的倒数组成。即把半带滤波器H进行分解后找到所有圆内的零点就可以确定分析低通滤波器h0,再按照PR条件即式关系依次求出分析高通滤波器h1,综合滤波器f1和f2。......
2023-06-23
相关推荐