同时随着长江沿线经济社会的发展，防洪、发电、航运、供水、减淤、生态、应急等方面对三峡水库调度提出了更高的需求。针对运行环境和调度需求的不断变化，若仍按初步设计的调度方式，三峡水库将不能较好地发挥综合利用效益。因此，为适应新的运行条件和调度需求，实现三峡水库的安全和高效运行，有必要进一步研究优化三峡水库调度运行方式。......
2025-09-29
优化泥沙配置目标函数
【摘要】：泥沙资源优化配置的处理方法与水资源优化配置是类似的，利用多目标函数的条件极值原理进行配置。若考虑泥沙资源优化配置对各种效益的作用及平衡分配原则，则综合目标函数为式中:Rij为目标权重系数，根据配置单元对目标效益的贡献情况来确定。流域泥沙配置的约束条件表示为式中:akj为第j 个目标函数下第k 个约束条件 (k=1，2，…当泥沙表现为灾害时，采用泥沙灾害损失最小为泥沙优化配置的目标函数。
泥沙资源优化配置的目标是兼顾泥沙资源开发利用的当前和长远利益、兼顾不同地区与部门间的利益，兼顾泥沙资源开发利用的社会、经济和环境利益，以及兼顾效益在不同受益者之间的分配，使得泥沙资源配置的效益最大、产生的泥沙灾害最小。泥沙资源优化配置的处理方法与水资源优化配置是类似的，利用多目标函数的条件极值原理进行配置。
在流域内，泥沙配置单元包括流域水土保持拦沙、水库拦沙、河道滞沙、引沙用沙及河道排沙等 (胡春宏，王延贵等，2003)。设不同泥沙配置单元的沙量为X，当泥沙表现为资源性时，仅考虑泥沙配置在经济、社会和环境等方面所产生的效益，泥沙配置的目标是以其效益最大为基本目标度量值，泥沙配置的度量函数可表示为
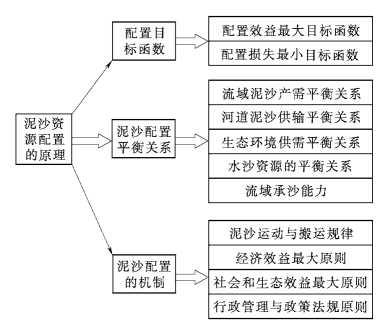
图12-4 流域泥沙资源配置的原理框图
式中:Zj为第j 个目标的函数值，共有m 个目标函数;i为泥沙配置单元序号;n 为泥沙配置单元数;C 为泥沙配置单元的效率系数，这一系数与泥沙配置内容、配置地域等有重要的关系;f 为反映配置沙量所产生效益的函数关系，它代表泥沙资源配置和利用对于经济、社会和生态环境效益的转化能力。
显然，这是一个度量经济、社会和环境效益协调发展的多目标问题，目标间的竞争性和具体量化问题则是一个多目标决策问题。泥沙配置单元产生的直接经济效益、间接社会和生态环境效益又可分为很多子类效益，例如就业机会、粮食产量、水质净化、土地沙化、湿地、防洪、造地面积等。泥沙资源优化配置对产生经济效益、社会效益和生态环境效益的作用是不同的，对上述子类效益的作用也是不同的。若考虑泥沙资源优化配置对各种效益的作用及平衡分配原则，则综合目标函数为
式中:Rij为目标权重系数，根据配置单元对目标效益的贡献情况来确定。
在流域泥沙实际配置过程中，实现上述目标将受到很多条件的约束，如社会经济条件、流域承沙能力等。流域泥沙配置的约束条件表示为(https://www.chuimin.cn)
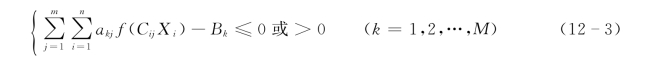
式中:akj为第j 个目标函数下第k 个约束条件 (k=1，2，…，M;M 为控制条件数)的水沙系数;Bk为各约束条件的效益控制量或者区域承沙能力。
显然，流域泥沙资源优化配置问题就演变为求解多目标函数的条件极大值问题，数学方程组由综合目标函数式(12-2)和配置约束条件式(12-3)两部分组成，求解方程组便得到一个最优和拟最优的规划方案。
当泥沙表现为灾害时，采用泥沙灾害损失最小为泥沙优化配置的目标函数。泥沙造成的损失又可以分为直接经济损失、社会恶劣影响和生态环境破坏。综合目标函数为
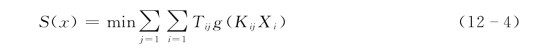
约束条件为
式中:S 为综合目标的函数值;Tij为目标权重系数;j、i分别为泥沙配置目标函数和配置单元序号;K 为泥沙配置单元的效率损失系数，这一系数与泥沙配置内容、配置地域等有重要的关系;g 为用沙量所产生灾害损失的函数关系，它代表泥沙资源配置和利用对于经济、社会和生态环境产生的影响;ckj为第j 个目标函数下第k 个约束条件 (k=1，2，…，M;M 为控制条件数)的系数;Ek为各约束条件的损失控制量或者区域承沙能力。
同样，流域泥沙资源优化配置问题就演变为求解多目标函数的条件极小值问题，求解由综合目标函数式(12-4)和约束条件式(12-5)的方程组，便得到泥沙灾害损失最小的泥沙配置规划方案。
相关文章
- 详细阅读
-
汛限水位调度目标优化详细阅读
汛限水位优化调度的目的，就是在平衡各运用目标要求的前提下，充分利用弃水，进一步发挥水库综合效益。在求解上述三峡水库汛限水位调度优化问题时，可根据约束法将多目标优化问题转变为单目标优化问题。在防洪目标和下游航运目标转化为约束条件后，三峡水库汛限水位优化调度目标转换为:在不降低目前防洪标准和改善下游航运条件的前提下，获取最大的发电及上游航运综合效益。......
2025-09-29
-
梯级系统的设计与配置优化详细阅读
一般采用F级绝缘、IP54外壳保护等级。各品牌对公共交通型自动扶梯的动力配置不尽相同，但一般以80%左右的制动载荷作为额定载荷计算电动机功率，通常比普通自动扶梯高20%以上。减速箱 普通自动扶梯多采用造价较低的单级蜗轮蜗杆减速箱。常采用的有全齿轮减速箱、一级齿轮一级蜗轮的减速箱。减速箱的工作寿命设计应不小于140000h。梯级链条的安全系数应不小于5。一般要求在制动载荷条件下，销轴比压不大于25N/mm2。......
2025-09-29
-
流域水沙资源的优化配置理论框架详细阅读
图12-1流域水沙资源优化配置 (调控)的理论体系流域泥沙的资源化及其途径。流域水沙资源优化配置的控制条件主要包括产流产沙关系、输沙量与径流量之间的关系、水沙运动输移方程、水沙分配关系、工程与技术控制条件等。根据上述流域水沙资源优化配置的理论，建立流域水沙资源优化配置的数学模型，包括河床演变均衡稳定模型和水沙资源多目标优化配置模型两个子模型，并应用于黄河下游。......
2025-09-29
-
二维水流泥沙模型验证的优化方法详细阅读
5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时，比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口，如图5-74所示，是一个强潮型河口。......
2025-09-29
-
电气设备总体配置的优化设计方案详细阅读
总体配置设计是将控制系统划分为几个部件，再进一步划分为若干组件，如开关组件、控制电器组件、电源组件等，并同时要解决组件之间、电气箱之间以及电气箱与被控制装置之间的连线问题。电气箱与被控制设备或电气箱之间采用多孔接插件，便于拆装、搬运。总体配置设计的合理与否将直接影响电气控制设备工作的可靠性，并关系到电气系统的制造、装配质量，调试、操作及维护是否方便。......
2025-09-29
-
优化光刻物镜评价函数的方法与应用详细阅读
先在ZEMAX镜头数据表中取三个视场，填写采用弥散圆型式的默认评价函数，并在其中增加如下操作，构成优化过程中的评价函数：{PMAG；Target，Weight}{PMAG；-0.25，100}{DIST；Target，Weight}{DIST；0，10}{DIMX；Target，Weight}{DIMX；0，10}{FCUR；Target，Weight}{FCUR（0；1）；0，10}{FCGT；Target，Weight}{FCGT；0，10}{FCGS；Target，Weight}{FCGS；0，10}在默认评价函数的第二视场中加入：{TRAC；Target，Weight}{TRAC；0，1}{TRAC；Target，Weight}{TRAC；0，1}在第三视场中加入：{TRAC；Target，Weight}{TRAC；0，1}{TRAC；Target，Weight}{TRAC；0，1}这个评价函数就是前面多次使用过的“新构造的评价函数”。......
2025-09-29
-
优化目标最优化算法之目估适线法详细阅读
图X3.11频率计算适线法框图统计参数的初适值，可用矩法公式计算、Cv，并假定Cs/Cv比值，也可采用三点法、概率权重矩法和双权函数法等。图X3.11频率计算适线法框图调整参数。试用适线法推求该站年降水量的频率曲线，并确定相应于频率为10%、50%、90%的年降水量。图X3.13某站年降水量频率曲线类似地，计算F列的模比系数以及G列ki-1和H列2数据，并对各列求和，其中F列的模比系数的总和应等于n，G列的总和应等于0，据此可进行校核。......
2025-09-29
相关推荐